Vorstellung des neuen Körpers "Pyramide"

1.1 Die Pyramide in unserer Umwelt

In unserer Umwelt besteht jeder Gegenstand - wenn man von leichten Veränderungen wie Abrundungen bei Schränken oder einem Henkel an einer Tasse absieht - aus geometrischen Körpern wie z.B. Kugel, Prisma, Quader oder Kegel.

In folgender Aufgabe siehst du einige Beispiele:

Geometrische Körper in unserer Umwelt
Ordne die Bilder und die Begriffe jeweils richtig zu.

Quader

Kegelstumpf

Kugel

Zylinder(Halb-)KugelKegel

Schüler betrachten die Pyramide in der Schule grundsätzlich als einen neuen - zunächst unbekannten - Körper, den sie höchstens von den ägyptischen Pyramiden kennen.
Doch bei näherer Betrachtung umgibt die Pyramide uns häufiger als wir es glauben mögen.

1.2 Definition

Verbindet man die Eckpunkte eines n-Ecks mit einem Punkt S außerhalb der Ebene des n-Ecks, so entsteht eine                     . Das n-Eck heißt                     und S heißt                     der Pyramide.

Der Abstand der Spitze von der Grundfläche heißt                     . Die Seiten der Grundfläche heißen                     , die Verbindungsstrecken der Eckpunkte der Grundfläche mit der Spitze sind die                     . Die Seitenflächen sind immer                     , die zusammen die                     bilden. Ihren Inhalt bezeichnet man kurz mit M.

DreieckeGrundflächen-seitige PyramideSpitzeMantelflächeSeitenkantenGrundkantenHöhe

1.3 Pyramidenarten

1.3.1 Gerade / Schiefe Pyramide

Pyramiden unterscheiden sich nicht nur in der Anzahl der Seiten bzw. der Ecken der Grundfläche.
Man unterscheidet auch zwischen geraden und schiefen Pyramiden:

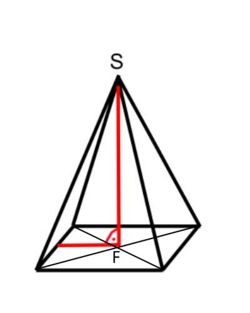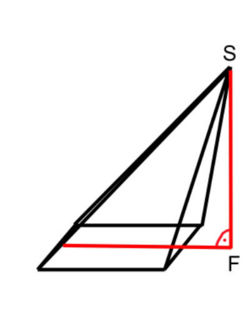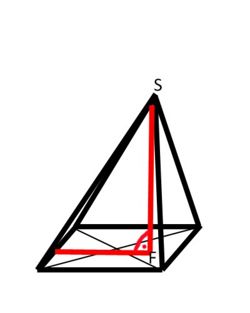
gerade Pyramide	schiefe Pyramiden

Was ist deiner Meinung nach das Kriterium für eine schiefe bzw. gerade Pyramide?

Fülle die Lücken aus! Das Lösungswort steht jeweils verdreht hinter der Lücke:

Eine gerade Pyramide zeichnet sich dadurch aus, dass die Höhe der Pyramide (ehbnnrlia)

liegt, und der Höhenfußpunkt F mit dem (ktnimttupel) der Grundfläche zusammenfällt.

Also liegt die Spitze S (rscknhete) über dem Mittelpunkt der (dnlhucägfre).

Dagegen ist eine Pyramide schief, wenn die Spitze S nicht senkrecht über dem Mittelpunkt der Grundfläche

liegt. Dabei kann die Höhe sogar (uehlaaßbr) der Pyramide liegen, so dass der (ßkuftunpöhneh) F nicht in der (dglhernäucf) G liegt.

1.3.2 Grundfläche und Höhe als Kriterium

Wie wir soeben erfahren haben, können schiefe und gerade Pyramiden unterschieden werden.

Pyramiden können aber auch nach ihrer Grundfläche oder Höhe unterschieden werden.

Beispiele:

• Pyramide mit vier gleichseitigen Dreiecken als Grund- und Seitenflächen (Diese Pyramide wird auch Tetraeder genannt)
• Pyramiden mit einem regelmäßigem 17-Eck, 20-Eck oder 24-Eck als Grundfläche
• Zwei Pyramiden mit identischen trapezförmigen Grundflächen jedoch mit unterschiedlichen Höhen

Pyramiden mit gleichem Grundflächeninhalt und gleicher Höhe sind volumengleich. Sind ihre Grundflächen sogar kongruent (dechkungsgleich), sind die Pyramiden identisch.
Ob Pyramiden mit gleichem Grundflächeninhalt volumengleich sind, hängt zusätzlich von den Pyramidenhöhen ab.