Benutzer:WR7d09
Hallo lieber Besucher
Heute wollen wir was über die Drehung und der Achsenspiegelung berichten:
Die Drehung:
Bei einer Drehung...
- handelt es sich um eine Ersatzabbildung einer Doppelachsenspiegelung an zwei Achsen - der Umlaufsinn wird nicht geändert - die Drehung ist eine gleichsinnige Kongruenzabbildung - gibt es nur einen Fixpunkt - der Urpunkt hat die gleiche Entfernung zum Drehpunkt wie der Bildpunkt
Wenn eine Figur an zwei sich schneidenden Geraden gespiegelt wird...
- dann lässt sich die Urfigur durch eine Drehung in die 2. Bildfigur überführen - dann lässt sich die Urfigur durch eine Drehung in die 2. Bildfigur überführen, dabei ist der Drehwinkel doppelt so groß wie der Winkel zwischen den Geraden - dann ist der Winkel zwischen den Geraden doppelt so groß wie der Drehwinkel, der benötigtt wird, um die Urfigur in die zweite Bildfigur zu überführen
Die Drehung wird bestimmt durch den Drehwinkel und das Drehzentrum.
Die Achsenspiegelung:
Eine Achsenspiegelung ist geradentreu, deshalb bleibt eine Gerade nach der Achsenspiegelung Gerade. außerdem ist sie längengetreu und winkelgetreu, das heißt, das Winkelmaß eines Winkels ändert sich nach der Achsenspiegelung nicht.
Wenn man ein Dreieck an einer Gerade spiegelt wird der Umlaufsinn umgekehrt und die Verbindungstrecke zwischen dem Ur- und Bildpunkt ist senkrecht zur Spiegelachse. Der Urpunkt hat die gleiche Entfernung zur Spiegelachse wie der Bildpunkt.
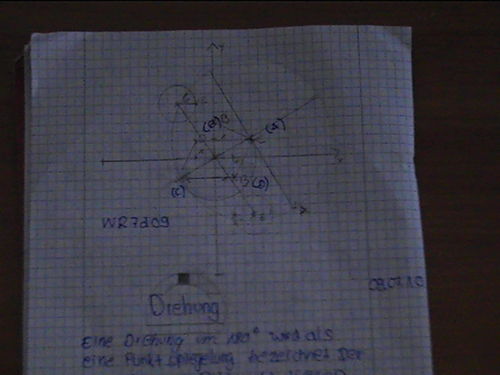
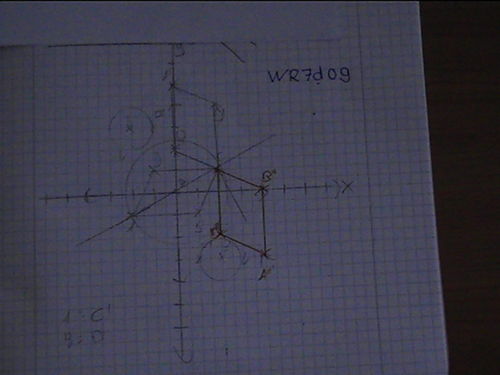
Die Zeichnungen aus dem Heft: