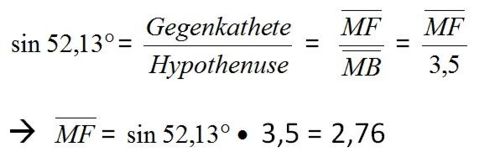Lösungsansatz
Aufgabe: Berechne die Mantelfläche
Die Mantelfläche setzt sich aus den Dreiecken zusammen, die die Grundkanten
jeweils mit zwei anliegenden Seitenkanten einschließen. Sie besitzen alle die gleiche Spitze S.
Um die Dreiecksflächen berechnen zu können, benötigst du die Dreieckshöhen.
In diesem Lösungsansatz erfährst du, wie man die Höhe des Dreiecks BCS errechnen kann:
1. Zunächst legst du den letzten Schalter (blau) oben im Applet um, um das nötige Stützdreieck MFS anzuzeigen.
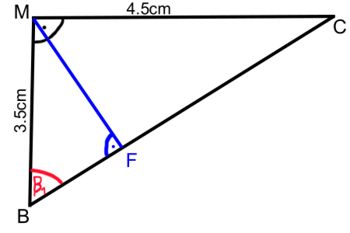
2. Als nächstes betrachten wir das Dreieck BCM:
Nun berechnest du den Winkel ![]() im rechtwinkligen Dreieck BCM wiefolgt:
im rechtwinkligen Dreieck BCM wiefolgt:
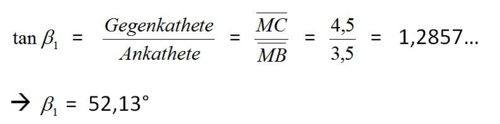
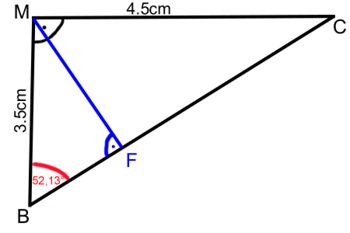
3. Nun berechnest du die Höhe ![]() des Dreiecks BCM. Dazu betrachten wir das Teildreieck BFM genauer:
des Dreiecks BCM. Dazu betrachten wir das Teildreieck BFM genauer:
Die Hypothenuse ![]() = 3,5cm ist gegeben und die Seite MF ist die Gegenkathete zum Winkel
= 3,5cm ist gegeben und die Seite MF ist die Gegenkathete zum Winkel ![]() , also rechnest du MF wiefolgt:
, also rechnest du MF wiefolgt:
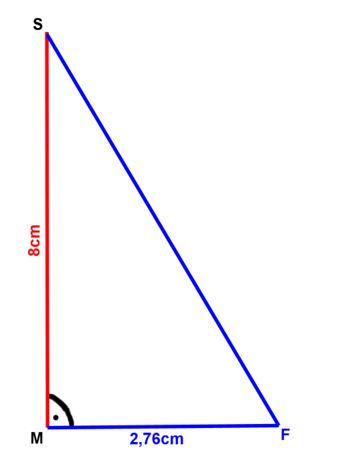
4. Nun wird letzlich noch das eingeblendete Stützdreieck MFS genauer betrachtet:
In diesem rechtwinkligen Dreieck entspricht die Hypothenuse der gesuchten Dreieckshöhe ![]() .
.
Mit Hilfe des Satz des Pythagoras sieht die Rechnung folgendermaßen aus:
Damit lässt sich nun die Fläche des Dreiecks BCS berechnen.
Gehe nun zurück. Fahre nun analog selbständig mit der Berechnung der Mantelfläche fort!