Die Quadratische Funktion der Form f(x) = a(x-d)² + e und die Normalform f(x) = ax² + bx + c
|
Lernpfad
|
Aus den vorherigen Lerneinheiten kennst du die Eigenschaften der einzelnen Parameter.
Du weißt zum einen, dass der Vorfaktor a für die Streckung und Stauchung der Parabel verantwortlich ist, und zum anderen, dass die Parameter d und e eine Verschiebung der Parabel in der Ebene bewirken.
Wir betrachten nun die Scheitelpunktsform mit dem Vorfaktor a.
 a(x - d)² + e
a(x - d)² + e
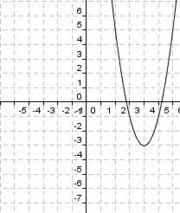
Im Folgenden bekommst du einen Graphen vorgegeben, mit dessen Hilfe du den Lückentext ausfüllen und so dein bisher gelerntes Wissen überprüfen und festigen kannst.
Achtung: Solltest du feststellen, dass dir Wissen fehlt, gehe bitte zu den vorherigen Lerneinheiten zurück und frische dein Wissen auf!
Quadratische Funktion f(x) a(x-d)2+ e a(x-d)2+ e |
Aufgabenstellung und Lückentext: |
|---|---|
|
Aufgabenstellung:
Ist der Vorfaktor a positiv, so ist der Graph nach oben geöffnet, ist er negativ, so ist er nach unten geöffnet. Für 0 < a < 1 ist der Graph weiter geöffnet als die Normalparabel, wohingegen bei a > 1 der Graph enger wird. Für -1 < a < 0 ist der Graph weiter als die Normalparabel und für a < -1 wird der Graph enger. Den tiefsten bzw. den höchsten Punkt einer Parabel nennt man Scheitelpunkt. Dieser ist abhängig von den Parametern d und e. Beide Parameter sind für eine Verschiebung der Parabel in der Ebene verantwortlich. Während der Parameter e die Parabel entlang der y-Achse verschiebt, sorgt der Parameter d für eine Verschiebung entlang der x-Achse.
Nach oben und rechts verschoben wird für positive Werte der Parameter e und d. Nach unten und links verschoben wird für negative Werte der Parameter e und d. Nach oben und links wird verschoben, wenn der Parameter e positiv und der Parameter d negativ ist. Nach unten und rechts verschoben wird, wenn der Parameter e negativ und der Parameter d positiv ist. |
Das hat mit Sicherheit ganz gut geklappt!
Im folgenden Merke werden die wichtigsten Eigenschaften nochmal auf den Punkt gebracht.
Wiederholung der wichtigsten Eigenschaften:
|
Für die quadratische Funktion f(x)
|
Nachdem du nun dein Wissen aufgefrischt hast, kann es auch gleich geübt werden!
 a(x - d)2 + e
a(x - d)2 + e
1. Aufgabe:
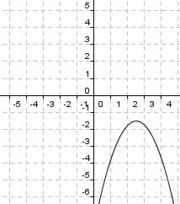
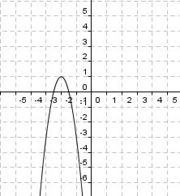
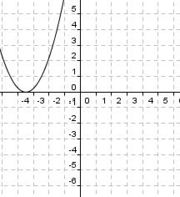
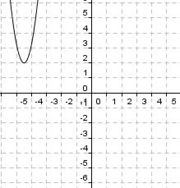
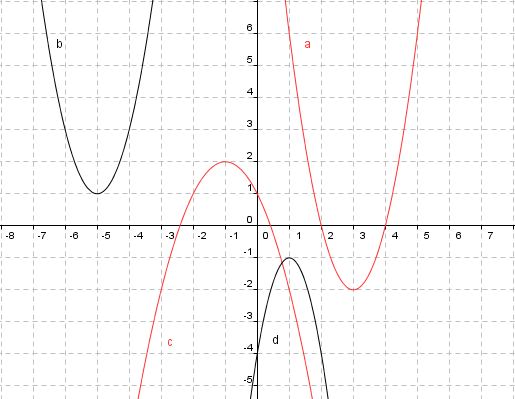
Du siehst hier ein paar Graphen und ein paar Funktionsvorschriften der Form
f(x)  a(x - d)2 + e. Versuche jeweils die richtigen Päärchen zu finden.
a(x - d)2 + e. Versuche jeweils die richtigen Päärchen zu finden.
Ich nehme an, dass das kein Problem für dich war, da man nicht unbedingt den Vorfaktor a bestimmen musste, um die Aufgabe zu lösen.
Jetzt wollen wir das Ganze ein wenig erschweren!
Kannst du dich noch erinnern, wie man den Vorfaktor a bestimmt?
2. Aufgabe:
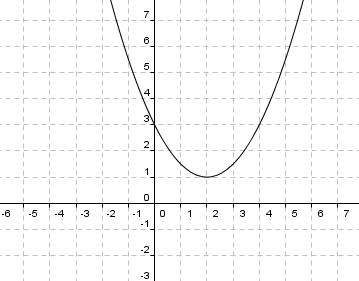
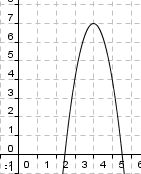
Finde zu den vorgegebenen Graphen die Funktionsvorschrift und gib den Scheitelpunkt an!
Falls du nicht genau weißt wie du vorgehen sollst, öffne die Hilfe!
Hilfe:
1. Scheitelpunkt ablesen für die Parameter d und e: S 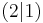
2. Vorfaktor a bestimmen:
- beliebige Koordiante aussuchen (nicht Scheitelpunkt): z.B. Punkt P
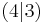
- Einsetzen der Werte in die Gleichung: 3
 a (4 - 2)2 + 1
a (4 - 2)2 + 1
- Ausrechnen und umstellen ergibt: a
 0,5
0,5
3. Funktionsvorschrift lautet: f(x)  0,5 (x - 2)2 + 1
0,5 (x - 2)2 + 1
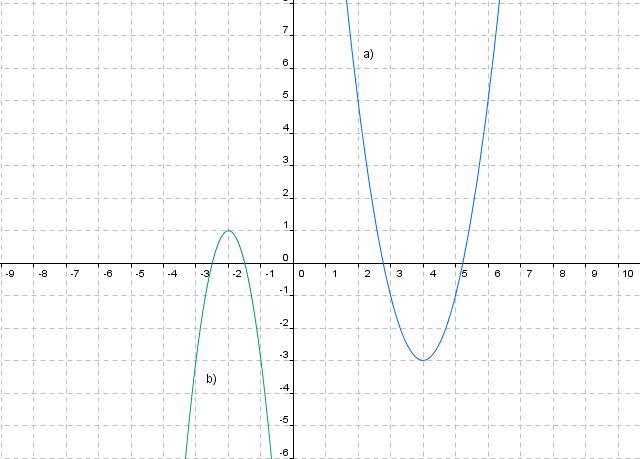
Lösung:
a) f(x)  2(x - 4)2 - 3
2(x - 4)2 - 3
b) f(x)  -4(x + 2)2 + 1
-4(x + 2)2 + 1
3. Aufgabe - Multiple Choice:
Betrachte die Funktionsvorschriften genau und kreuze die richtigen Aussagen an. Achtung! Es können auch mehrere Antworten richtig sein!
f(x)  -2x2 + 5 (!Die Parabel ist nach oben geöffnet)(Die Parabel ist nach unten geöffnet)(Die Parabel hat den höchsten Punkt bei [0, 5]) (Die Parabel ist enger als die Normalparabel) (!Die Parabel ist weiter als die Normalparabel) (!Die Parabel ist um 2 Einheiten nach links verschoben)
-2x2 + 5 (!Die Parabel ist nach oben geöffnet)(Die Parabel ist nach unten geöffnet)(Die Parabel hat den höchsten Punkt bei [0, 5]) (Die Parabel ist enger als die Normalparabel) (!Die Parabel ist weiter als die Normalparabel) (!Die Parabel ist um 2 Einheiten nach links verschoben)
f(x)  (x - 3)2 - 2 (!Die Parabel ist weiter als die Normalparabel)(!Die Parabel hat den tiefsten Punkt bei [0, -2])(Die Parabel verläuft durch den Punkt [0, 7]) (!Die Parabel ist um 3 Einheiten nach links verschoben) (Die Parabel ist kongruent zur Normalparabel) (Die Parabel ist um drei Einheiten nach rechts verschoben)
(x - 3)2 - 2 (!Die Parabel ist weiter als die Normalparabel)(!Die Parabel hat den tiefsten Punkt bei [0, -2])(Die Parabel verläuft durch den Punkt [0, 7]) (!Die Parabel ist um 3 Einheiten nach links verschoben) (Die Parabel ist kongruent zur Normalparabel) (Die Parabel ist um drei Einheiten nach rechts verschoben)
f(x)  6 + 2 (x + 2)2 (!Die Parabel ist nach unten geöffnet)(!Die Parabel wurde um 2 Einheiten nach rechts verschoben)(Die Parabel ist nach oben geöffnet ) (Die Parabel wurde um 2 Einheiten nach links verschoben) (!Die Parabel ist weiter als die Normalparabel) (Die Parabel ist enger als die Normalparabel)
6 + 2 (x + 2)2 (!Die Parabel ist nach unten geöffnet)(!Die Parabel wurde um 2 Einheiten nach rechts verschoben)(Die Parabel ist nach oben geöffnet ) (Die Parabel wurde um 2 Einheiten nach links verschoben) (!Die Parabel ist weiter als die Normalparabel) (Die Parabel ist enger als die Normalparabel)
Die Parabel ist um 2 Einheiten nach links und um 4 Einheiten nach oben verschoben. Außerdem ist sie enger als die Normalparabel (!y  4 [x - 2]2 - 4)(!y
4 [x - 2]2 - 4)(!y  0,2 [x - 2]2 + 4)(!y
0,2 [x - 2]2 + 4)(!y  2 [x - 2]2 + 4)(y
2 [x - 2]2 + 4)(y  3 [x + 2]2 + 4)(!y
3 [x + 2]2 + 4)(!y  0,5 [x + 2]2 - 4)(!y
0,5 [x + 2]2 - 4)(!y  5 [x + 2]2 - 4)(!y
5 [x + 2]2 - 4)(!y  0,8 [x - 2]2 + 4)(y
0,8 [x - 2]2 + 4)(y  1,77 [x + 2]2 + 4)
1,77 [x + 2]2 + 4)
4. Aufgabe - KNIFFELAUFGABE:
Welche der folgenden Funktionsvorschriften hat eine Nullstelle? Achtung! Aufgabe nur durch logisches Denken lösen, keine Rechnung erforderlich!
a) f(x)2 (x - 3)2 - 2 b) f(x)
2 (x + 5)2 + 1 c) f(x)
- (x + 1)2 + 2 d) f(x)
-3 (x - 1)2 -1
Hilfe:
Falls du Hilfe brauchst, kannst du dir hier einen Tipp holen!
Lösung:
Die Teilaufgaben a) und c) sind richtige Lösungen.
Wie du in der Grafik sehen kannst, kommt es nur auf den Parameter e und den Vorfaktor a an.
Ist der Vorfaktor a positiv und der Parameter e zugleich negativ, so liegt der Scheitelpunkt der Parabel unterhalb der x-Achse. Da die Parabel durch den positiven Vorfaktor a nach oben geöffnet ist, muss es Nullstellen geben.
Genau umgekehrt verhält es sich für den Fall, dass der Vorfaktor a negativ und der Parameter e positiv ist.
 ax2 + bx + c
ax2 + bx + c
Zum Schluss des Lernpfades „Quadratische Funktionen“ wird die Normalform und ihre Herleitung vorgestellt.
Im Moment erkennt man noch kein Muster zwischen der Scheitelpunktsform f(x)  a(x - d)2 + e und der Normalform f(x)
a(x - d)2 + e und der Normalform f(x)  ax2 + bx + c. Das ist aber gar nicht schwer!
ax2 + bx + c. Das ist aber gar nicht schwer!
Es gibt zwei Betrachtungen:
1. Von der Scheitelpunktsform zur Normalform?
2. Von der Normalform zur Scheitelpunktsform?
Zunächst betrachten wir Punkt 1: Von der Scheitelpunktsform zur Normalform
Da es nicht besonders schwer ist, wirst du in der folgenden Aufgabe selbst den Zusammenhang zwischen der Scheitelpunktsform und der Normalform herstellen!
Aufgabe:
Du hast die Scheitelpunktsform f(x)  2(x - 4)2 + 5 gegeben.
Bring die quadratische Funktion f(x)
2(x - 4)2 + 5 gegeben.
Bring die quadratische Funktion f(x)  2(x - 4)2 + 5 durch ausmultiplizieren und zusammenfassen der
2(x - 4)2 + 5 durch ausmultiplizieren und zusammenfassen der
Terme auf die Form f(x)  ax2 + bx + c
ax2 + bx + c
Lösung:
f(x)2 (x - 4)2 + 5
2 (x2 - 8x + 16) + 5
2x2 - 16x + 32 + 5
2x2 - 16x + 37
|
Die Normalform f(x) |
Jetzt betrachten wir Punkt 2: Von der Normalform zur Scheitelpunktsform
Diese Umformung ist etwas schwieriger, aber du kennst sie schon von früher!
Aus den vorherigen Lerneinheiten weißt du über alle Eigenschaften der Scheitelpunktsform bescheid und welche Veränderungen sie an der Parabel vornehmen können
Da wir das von der Normalform „f(x) = ax2 + bx + c" nicht sagen können, müssen wir die Normalform in die Scheitelpunktsform umwandeln.
Keine Angst, die Vorgehensweise ist dir bekannt, sie nennt sich quadratische Ergänzung und du hast sie bei der Extremwertbestimmung kennen gelernt.
Zur Wiederholung klicke dich durch die folgende Anleitung:
„Von der Scheitelpunktsform zur Normalform“:
1. Schritt: Gegeben ist die Parabel p
2. Schritt: Faktor ausklammern
3. Schritt: Quadratische Ergänzung
4. Schritt: Binom erzeugen
5. Schritt: Äußere Klammer auflösen
6. Schritt: Scheitelkoordinaten
Mit Sicherheit hast du dich wieder an die quadratische Ergänzung erinnert und weißt nun wieder, wie man von der Normalform zur Scheitelpunktsform gelangt.
Um das ein wenig einzuüben löse die folgende Aufgabe!
Aufgabe: Zuordnung - Gruppe
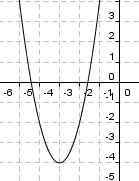
Nimm dir ein Blatt und stell zu den vorgegebenen quadratischen Funktionen die Scheitelpunktsform auf und ordne anschließend die richtigen Scheitelpunktsformen, Scheitelkoordinaten und Graphen der richtigen quadratischen Funktion zu.
f(x) 2x2 + 12x + 14 2x2 + 12x + 14 |
f(x) 2(x + 3)2 - 4 2(x + 3)2 - 4 |
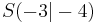 |
 |
|
f(x) -3x2 + 24x + -41 -3x2 + 24x + -41 |
f(x) -3(x - 4)2 + 7 -3(x - 4)2 + 7 |
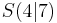 |
 |
|
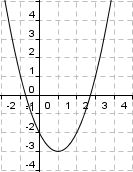
f(x) x2 - 2x - 2 x2 - 2x - 2 |
f(x) (x - 1)2 - 3 (x - 1)2 - 3 |
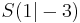 |
|
Lösung:
Falls du Probleme mit der quadratischen Ergänzung hattest kannst du sie dir hier anschauen!
f(x)2x2 + 12x + 14
2 [x2 + 6x] + 14
2 [x2 + 6x + 32 - 32] + 14
2 [(x + 3)2 - 32] + 14
2 (x + 3)2 - 2(32) + 14
2 (x + 3)2 - 18 + 14
2 (x + 3)2 - 4
f(x)-3x2 + 24x - 41
-3 [x2 - 8x] - 41
-3 [x2 - 8x + 42 - 42] - 41
-3 [(x - 4)2 - 42] - 41
-3 (x - 4)2 -[-3(-42)] - 41
-3 (x - 4)2 + 48 - 41
-3 (x - 4)2 + 7
f(x)x2 - 2x - 2
(x - 1)2 - 12 - 2
(x - 1)2 - 3
Jetzt kennst und kannst du wirklich alles zur quadratischen Funktion. Stelle dein Wissen in der vierten und letzten Station unter Beweis. Hier wird noch mal alles zuvor Erlernte in vermischten Aufgaben gefragt. Viel Erfolg!
1. Aufgabe: Schüttelrätsel
Finde die unverdrehte Lösung zu den verdrehten Wörtern!
Du kannst deine Ergebnisse erst überprüfen, wenn alle Felder ausgefüllt sind!
Eine Funktion der Form f(x) = ax2 + bx + c nennt man quadratische Funktion.
Durch Umformen mit Hilfe der quadratischen Ergänzung erhält man die Scheitelpunktsform f(x) = a(x - d)2 + e.
An der Scheitelpunktsform kann man die Koordinaten für den Scheitelpunkt ablesen.
Der Scheitelpunkt gibt dabei den höchsten oder tiefsten Punkt der Parabel an.
Hat die Parabel einen höchsten Punkt, so ist sie nach unten geöffnet und der Vorfaktor a vor dem x2 ist negativ.
Ist der Vorfaktor hingegen positiv, dann besitzt die Parabel einen tiefsten Punkt und die Parabel ist nach oben geöffnet.
Außerdem ist der Vorfaktor a noch für die Streckung oder Stauchung der Parabel verantwortlich.
Nimmt der Vorfaktor einen Wert zwischen -1 und +1 an, so wird die Parabel gestaucht.
Ist hingegen der Vorfaktor a kleiner -1 oder größer +1, so wird die Parabel gestreckt.
Neben der Streckung und Stauchung der Parabel durch den Vorfaktor a, existieren noch die Parameter d und e, die für eine Verschiebung der Parabel in der Ebene verantwortlich sind.
Dabei gilt, dass für e > 0 die Parabel nach oben auf der y-Achse verschoben wird und für e < 0 nach unten.
Ähnlich verhält es sich mit dem Parameter d, der für eine Verschiebung der Parabel auf der x-Achse sorgt.
Hier wird für d > 0 nach rechts auf und für d < 0 nach links verschoben.
2. Aufgabe: KNIFFELAUFGABE
Gegeben ist die Funktion f(x) = 0,5x2 - x - 2,5
Gib die Koordinaten an, an der die Funktion die y-Achse schneidet
Tipp!
Überlege dir, was gelten muss, wenn die Parabel y-Achse schneidet.
Hilfe:
Du kennst einen Koordinantenpunkt. An der Stelle, an der die Parabel die y-Achse schneidet ist der x-Wert 0. Setze diesen Wert in die Gleichung ein und bestimme den zugehörigen y-Wert.
Lösung:
S (0; -2,5)
Erklärung: Wenn die Parabel die y-Achse schneidet ist der y-Wert vorgegeben, er ist 0. Diesen Wert setzt man in die Funktionsgleichung ein und bestimmt den y-Wert.
y0,5x2 - x - 2,5 y
0,5(0)2 - 0 - 2,5 y
-2,5
3. Aufgabe: Multiple Choice
Für die Funktion f(x)  x2 + 2 gilt: (Die Parabel schneidet die y-Achse)(!Die Parabel schneidet die x-Achse)(Die Parabel hat den Scheitelpunkt [0, 2]) (!Die Parabel hat den Scheitelpunkt [2, 0]) (!Der Scheitelpunkt ist der Punkt an dem die Parabel die x-Achse schneidet)
x2 + 2 gilt: (Die Parabel schneidet die y-Achse)(!Die Parabel schneidet die x-Achse)(Die Parabel hat den Scheitelpunkt [0, 2]) (!Die Parabel hat den Scheitelpunkt [2, 0]) (!Der Scheitelpunkt ist der Punkt an dem die Parabel die x-Achse schneidet)
Diese Funktion ist keine quadratische Funktion: (!y  [x - 2]2)(y
[x - 2]2)(y  2x2 + 3 - 5x)(!y
2x2 + 3 - 5x)(!y  2x3 + 2x + 3) (y
2x3 + 2x + 3) (y  8 + 2x) (!y
8 + 2x) (!y  [x + 3][x - 3])
[x + 3][x - 3])
Für die Funktion f(x)  2x2 + 2x gilt: (Die Parabel geht durch den Koordinatenursprung)(!Die Parabel ist nach unten geöffnet)(Die Parabel schneidet die x-Achse zwei Mal) (Die Parabel ist gestaucht)
2x2 + 2x gilt: (Die Parabel geht durch den Koordinatenursprung)(!Die Parabel ist nach unten geöffnet)(Die Parabel schneidet die x-Achse zwei Mal) (Die Parabel ist gestaucht)
Für den Graph der Funktion f(x)  -2 [x + 3]2 - 2 gilt: (Der Graph geht nicht durch den Ursprung)(Der Graph ist identisch mit y
-2 [x + 3]2 - 2 gilt: (Der Graph geht nicht durch den Ursprung)(Der Graph ist identisch mit y  -2x2 -12x -20)(!Der Graph ist eine verschobene Normalparabel) (!Der Graph ist nach oben geöffnet) (!Der Graph ist nach oben geöffnet)
-2x2 -12x -20)(!Der Graph ist eine verschobene Normalparabel) (!Der Graph ist nach oben geöffnet) (!Der Graph ist nach oben geöffnet)
Welche der folgenden Parabeln hat den Scheitelpunkt S(3, -2)? (!y  2x2 + 3x + 3) (y
2x2 + 3x + 3) (y  -3[x - 3]2 - 2) (y
-3[x - 3]2 - 2) (y  5[x - 3]2 - 2) (!y
5[x - 3]2 - 2) (!y  12 [x + 3] - 2)
12 [x + 3] - 2)
Wenn die Parabel die x-Achse nicht schneidet, dann gilt: (!Die Parabel ist nach oben geöffnet) (Die Parabel ist nach unten geöffnet und der Parameter e ist positiv) (y  2[x - 5]2 - 2) (!y
2[x - 5]2 - 2) (!y  [x + 6]2)
[x + 6]2)