Eigenschaften der zentrischen Streckung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (→6. Station: Zusammenfassung) |
(Links angepasst) |
||
| (48 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
===Eigenschaften der zentrischen Streckung=== | ===Eigenschaften der zentrischen Streckung=== | ||
}} | }} | ||
| + | <br>[[Bild:Porzelt_Eigenschaften.jpg|right]] | ||
<br> | <br> | ||
| − | |||
<br> | <br> | ||
| + | <br> | ||
| + | :'''In diesem Lernpfad durchläufst du 7 Stationen. Sie sind wie folgt gegliedert:'''<br> | ||
| + | |||
| + | :1. Station: Fixelemente<br> | ||
| + | :[[/2.Station|2. Station: Geradentreue und Parallelentreue]]<br> | ||
| + | :[[/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]]<br> | ||
| + | :[[/4.Station|4. Station: Längenverhältnistreue]]<br> | ||
| + | :[[/5.Station|5. Station: Kreistreue]]<br> | ||
| + | :[[/6.Station|6. Station: Zusammenfassung]]<br> | ||
| + | :[[/7.Station|7. Station: Übung]] <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | + | <br> | |
| − | = | + | <br> |
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | ==1. Station: Fixelemente== | ||
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | + | [[Bild:Porzelt_Panto-2.jpg|left]] <br>Für k<math>\not=</math>1 gilt: | |
| − | + | :Das Streckungszentrum Z ist '''Fixpunkt''', da es immer auf sich selbst abgebildet wird. | |
| − | + | ||
</div> | </div> | ||
<br> | <br> | ||
| − | : | + | <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> |
| − | + | {| | |
| − | <ggb_applet height=" | + | |'''''Strecke die Gerade g, die Punkte A, B und C zentrisch um den Faktor k und ordne im nebenstehenden Text den richtigen Ausdruck in die passende Lücke:'''''<br><ggb_applet height="300" width="600" showResetIcon="true" filename="Porzelt_Fixgerade.ggb" />|| |
| − | + | | |
| − | + | ||
| − | + | ||
| − | + | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | A | + | Der Punkt A wird auf den Punkt '''A'''' abgebildet, so wie der Punkt B auf Punkt '''B'''' und Punkt C auf Punkt '''C''''. Alle Punkte verlaufen auf einer '''Geraden'''. Die Gerade g wird auf die Gerade '''g'''' abgebildet.<br> Geometrisch bedeutet dies: g '''=''' g'. |
| − | + | </div> | |
| − | + | |} | |
| − | + | ||
| − | + | ||
</div> | </div> | ||
<br> | <br> | ||
| − | + | <br> | |
| − | + | <br> | |
| + | Panto will auch etwas dazu sagen. Lass es dir anzeigen:<br> | ||
| + | {{Versteckt|1= | ||
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | :''' | + | [[Bild:Porzelt_Panto-2.jpg|left]] <br>Alle Geraden, die durch den Punkt Z verlaufen, sind '''Fixgeraden'''. Sie werden bei einer zentrischen |
| − | + | :Streckung auf sich selbst abgebildet. | |
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| + | }} | ||
<br> | <br> | ||
| − | + | <div align="left">[[/2.Station|<math>\Rightarrow</math> Weiter zur 2. Station: Geradentreue und Parallelentreue]]</div> | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </div> | + | |
| − | + | ||
| − | + | ||
Aktuelle Version vom 19. Dezember 2009, 15:57 Uhr
|
Lernpfad
|
- In diesem Lernpfad durchläufst du 7 Stationen. Sie sind wie folgt gegliedert:
- 1. Station: Fixelemente
- 2. Station: Geradentreue und Parallelentreue
- 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue
- 4. Station: Längenverhältnistreue
- 5. Station: Kreistreue
- 6. Station: Zusammenfassung
- 7. Station: Übung
1. Station: Fixelemente
| Strecke die Gerade g, die Punkte A, B und C zentrisch um den Faktor k und ordne im nebenstehenden Text den richtigen Ausdruck in die passende Lücke: |
Der Punkt A wird auf den Punkt A' abgebildet, so wie der Punkt B auf Punkt B' und Punkt C auf Punkt C'. Alle Punkte verlaufen auf einer Geraden. Die Gerade g wird auf die Gerade g' abgebildet. |
Panto will auch etwas dazu sagen. Lass es dir anzeigen:


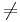 1 gilt:
1 gilt:
 Weiter zur 2. Station: Geradentreue und Parallelentreue
Weiter zur 2. Station: Geradentreue und Parallelentreue
