SWS-Satz-2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (hat „Benutzer:Kathrin Fuchs/SSS und SWS/Teil 5/6.Teil des 2.Lernpfades“ nach „Benutzer:Kathrin Fuchs/SSS und SWS/Teil 6“ verschoben: kürzer) |
K |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation SSS und SWS}} | ||
| + | |||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Zeile 6: | Zeile 9: | ||
<br /> | <br /> | ||
Lass uns ein paar Aufgaben dazu machen:<br /> | Lass uns ein paar Aufgaben dazu machen:<br /> | ||
| − | {{Aufgabe-Mathe|Konstruiere die folgenden Dreiecke mit GeoGebra und notiere die Konstruktionsbeschreibung auf deinem <u>Laufzettel</u> | + | {{Aufgabe-Mathe|Konstruiere die folgenden Dreiecke mit GeoGebra und notiere die Konstruktionsbeschreibung auf deinem <u>Laufzettel</u>:<br /> |
''Du findest ein Konstruktionsprotokoll im Menu unter '''ANSICHT''''' | ''Du findest ein Konstruktionsprotokoll im Menu unter '''ANSICHT''''' | ||
<br /> | <br /> | ||
| Zeile 17: | Zeile 20: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | + | ||
| + | [[Benutzer:Kathrin_Fuchs/SSS_und_SWS/SWS-Satz-3|<math>\Rightarrow</math> Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast vergleiche hier dein Ergebnis.]]. | ||
Aktuelle Version vom 19. Februar 2010, 23:37 Uhr
Lernpfad SSS und SWS: SSS-Satz - SSS: Aufgaben - SSS: Lösungen - SWS-Satz - SWS: Aufgaben - SWS: Lösungen - Weitere Aufgaben
 |
Wir wissen jetzt also, wie man Dreiecke eindeutig konstruiert wenn man die Länge von zwei Seiten und den einschließenden Winkel kennt. |
Lass uns ein paar Aufgaben dazu machen:
|
Konstruiere die folgenden Dreiecke mit GeoGebra und notiere die Konstruktionsbeschreibung auf deinem Laufzettel: |
Öffne dazu das GeoGebra-Fenster mit Doppelklick auf das Applet!
 4,8 cm, b
4,8 cm, b 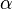
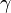
 Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast vergleiche hier dein Ergebnis.
Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast vergleiche hier dein Ergebnis.
