Quadratische Funktionen: Unterschied zwischen den Versionen
(→Quadratische Funktionen und Klippenspringen: Quellcode eingegeben) |
|||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | ||
| − | {{ | + | {| border="0" cellpadding="5" cellspacing="2" style="border: 1px solid {{{Rand|#ca1321}}}; background-color: {{{Hintergrund|#ffffff}}}; border-left: 5px solid {{{RandLinks|#ca1321}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}" |
| + | |- | ||
| + | | <div style="float:right; margin:0px; margin-top:5px">[[Bild:Maehnrot.jpg|100px]]</div> | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Merke:</div> | ||
| + | |||
| + | Die Graphen von Funktionen mit der Funktionsgleichung '''f(x)=x²''' heißen '''Parabeln'''. | ||
| + | |||
| + | Sie lassen sich auch in der Form '''y=x²''' darstellen. | ||
Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | ||
| − | } | + | |} |
| + | |||
<br /> | <br /> | ||
Schön, nun wissen wir, dass wir es mit Parabeln zu tun haben. Diese sind jedoch nicht immer in der starren Form f(x)=x² dargestellt. In der folgenden Aufgabe kannst du diese Parabel durch Schieben des Punktes auf dem Schieberegler [[Bild:Schieberegler.bmp]] verändern. | Schön, nun wissen wir, dass wir es mit Parabeln zu tun haben. Diese sind jedoch nicht immer in der starren Form f(x)=x² dargestellt. In der folgenden Aufgabe kannst du diese Parabel durch Schieben des Punktes auf dem Schieberegler [[Bild:Schieberegler.bmp]] verändern. | ||
| Zeile 36: | Zeile 44: | ||
</div> | </div> | ||
<br\> | <br\> | ||
| − | + | [[Bild:Laufzettel.png|50px]] Notiere eine mögliche Sprungbahn auf deinem Laufzettel! | |
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| Zeile 72: | Zeile 80: | ||
| − | + | <br\> | |
| + | [[Bild:Laufzettel.png|50px]] Bewerte die Aufgaben jetzt auf deinem Laufzettel! | ||
| + | <br\> | ||
Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen. | Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen. | ||
| − | + | <br> | |
| − | <div algin="left">[[Variationen/Quadratische Funktionen2/Übungen zu a|<math>\Rightarrow</math> Nächste Seite]]</div> | + | <big><div algin="left">[[Variationen/Quadratische Funktionen2/Übungen zu a|<math>\Rightarrow</math> Nächste Seite]]</div></big> |
| + | <br> | ||
<br> | <br> | ||
<div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | <div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | ||
Aktuelle Version vom 9. März 2010, 00:58 Uhr
Quadratische Funktionen und Klippenspringen
Aufgabe 5
![]() Notiere eine mögliche Sprungbahn auf deinem Laufzettel!
Notiere eine mögliche Sprungbahn auf deinem Laufzettel!
|
Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktion erhält also eine neue Gleichung:
Aufgabe 6Hast du mit a etwas experimentiert? Ist a = 1, so nennt man den Graphen Normalparabel. Ist a > 1, dann ist die Parabel enger (gestreckt) als die Normalparabel. Für 0 < a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel. Ist a negativ, so ist die Parabel nach unten geöffnet . Hast du die Aufgabe gelöst? Präge dir die jeweilige Auswirkung von a gut ein!
|
|
![]() Bewerte die Aufgaben jetzt auf deinem Laufzettel!
Bewerte die Aufgaben jetzt auf deinem Laufzettel!
Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen.

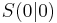 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
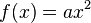 .
Mit der Manipulation des Schiebereglers hast du den Parameter a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
.
Mit der Manipulation des Schiebereglers hast du den Parameter a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
 Nächste Seite
Nächste Seite Zurück zur Übersicht
Zurück zur Übersicht
