Lineare Gleichungssysteme grafisch lösen/Station 2: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
(13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
 
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
−
[[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|1. Station]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|2. Station]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|3. Station]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|4. Station]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|5. Station]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|6. Station]]   
+
'''Inhaltsverzeichnis:''' &nbsp;&nbsp;  [[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|1. Einführung]] &nbsp;- &nbsp;[[Lineare Gleichungssysteme grafisch lösen/Station 2|2. Grafisches Lösungsverfahren]]&nbsp; - &nbsp;[[Lineare Gleichungssysteme grafisch lösen/Station 3|3. Übung zum grafischen Lösungsverfahren]]&nbsp; - &nbsp;[[Lineare Gleichungssysteme grafisch lösen/Station 4|4. Verschiedene Lösungsmöglichkeiten]] &nbsp;- &nbsp;<br>
 +
[[Lineare Gleichungssysteme grafisch lösen/Station 5|5. Memo-Quiz zu verschiedene Lösungsmöglichkeiten]]&nbsp; - &nbsp;[[Lineare Gleichungssysteme grafisch lösen/Station 6|6. Eine, keine oder unendlich viele Lösungsmöglichkeiten?]]   
 
</div>
 
</div>
  
−
=Station 2=
+
=2. Grafisches Lösungsverfahren=
  
 
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;">
Zeile 9: Zeile 10:
 
[[Bild:Motivation_Hatos_3.PNG|300px|center]]
 
[[Bild:Motivation_Hatos_3.PNG|300px|center]]
  
−
Wie du siehst kann man ein Lineares Gleichungssystem grafisch lösen.<br>
+
Wie du siehst kann man ein lineares Gleichungssystem grafisch lösen.<br>
 
Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören, in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen.  
 
Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören, in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen.  
  
−
''Versuche nun das folgende Lineare Gleichungssystem zu lösen:''
+
''Versuche nun das folgende lineare Gleichungssystem zu lösen:''
  
  
Zeile 42: Zeile 43:
 
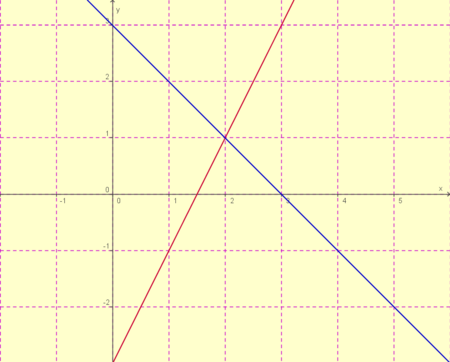
Die blaue Gerade gehört zu folgender Gleichung: (y = - x + 3) (!y = 2x - 3)
 
Die blaue Gerade gehört zu folgender Gleichung: (y = - x + 3) (!y = 2x - 3)
  
−
Wie lautet der Schnittpunkt der beiden Geraden? (![ 1 | 2 ]) ([ 2 | 1 ]) (![ 3 | 0 ])
+
3. Schritt: Wie lautet der Schnittpunkt der beiden Geraden? (![ 1 | 2 ]) ([ 2 | 1 ]) (![ 3 | 0 ])
 
</div>
 
</div>
 
|}
 
|}
Zeile 49: Zeile 50:
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
  
−
3. Schritt: Mache die Probe. Setze die Koordinaten des Schnittpunktes (siehe 2. Schritt) in deine beiden Anfangsgleichungen ein.  
+
4. Schritt: Mache die Probe. Setze die Koordinaten des Schnittpunktes (siehe 3. Schritt) in deine beiden Anfangsgleichungen ein.  
  
−
Ziehe hierfür mit gehaltener linker Maustaste die richtigen Zahlen in die freien Felder.
+
Ziehe hierfür mit gehaltener linker Maustaste die richtigen Zahlen in die freien Felder und klicke anschließend auf <span style="color: #FF0000">prüfen</span>!
  
 
Gleichung 1:  
 
Gleichung 1:  
Zeile 87: Zeile 88:
 
Diese Aussage ist '''wahr'''
 
Diese Aussage ist '''wahr'''
  
−
Also lautet die Lösung dieses Linearen Gleichungssystems
+
Also lautet die Lösungsmenge dieses linearen Gleichungssystems:
  
 
L = {('''2'''/'''1''')}   
 
L = {('''2'''/'''1''')}   
Zeile 97: Zeile 98:
  
 
</div>
 
</div>
 +
 +
 +
'''Lies dir den Merkekasten sorgfältig durch!'''
  
  
Zeile 103: Zeile 107:
 
{|
 
{|
 
|-
 
|-
−
|[[Bild:Hatos_Merke.PNG|250px]] || '''<div style="color:#0000CD ">Das grafische Lösungsverfahren!</div>'''
+
|[[Bild:Hatos_Merke.PNG|250px]] || '''<div style="color:#0000CD ">Das grafische Lösungsverfahren!</div>'''<br>
−
 
+
<br>
 
'''1.Schritt:''' Löse beide Gleichungen nach y auf, um jeweils die Form y = mx + t zu erhalten.
 
'''1.Schritt:''' Löse beide Gleichungen nach y auf, um jeweils die Form y = mx + t zu erhalten.
−
 
+
<br>
 +
<br>
 +
<br>
 +
<br>
 
'''2.Schritt:''' Zeichen die Geraden zu den beiden Funktionsgleichungen in ein Koordinatensystem.
 
'''2.Schritt:''' Zeichen die Geraden zu den beiden Funktionsgleichungen in ein Koordinatensystem.
−
 
+
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 
'''3.Schritt:''' Lies die Koordinaten des Schnittpunkts der beiden Geraden ab.  
 
'''3.Schritt:''' Lies die Koordinaten des Schnittpunkts der beiden Geraden ab.  
 +
<br>
 +
<br>
 +
<br>
 +
'''4.Schritt:''' Mache die Probe (mit beiden Ausgangsgleichungen) und gib dann die Lösungsmenge an.
 +
<br>
 +
<br>
 +
||<span style="color: #00CD66" > Beispiel:
 +
( I ) y + x = 4 und ( II ) 2y = x – 1
 +
<br>
 +
<br>
 +
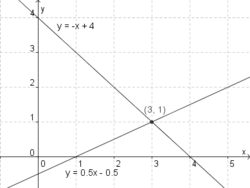
( I ) y = -x + 4<br>
 +
( II ) y = ½ x – ½
 +
 +
[[Bild:Grafisch.png|250px]]
 +
 +
 +
S (  3 | 1 )
 +
 +
 +
( I ) 1 + 3 = 4 (wahr)<br>
 +
( II ) 2 * 1 = 3 – 1 (wahr)
 +
 +
L = { ( 3 | 1 ) }
  
−
'''4.Schritt:''' Mache die Probe (mit beiden Ausgangsgleichungen) und gib dann die Lösungsmenge an.
+
</span>
 
|}
 
|}
 
</div>
 
</div>
Zeile 117: Zeile 154:
  
  
−
'''<big>→[[Lineare Gleichungssysteme grafisch lösen/Station 3|Hier gehts zur 3. Station]]</big>'''
+
'''<big>→[[Lineare Gleichungssysteme grafisch lösen/Station 3|Hier gehts weiter]]</big>'''
  
−
[[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|Hier gehts zurück zur 1. Station]]
+
[[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|Hier gehts zurück]]

Aktuelle Version vom 17. März 2010, 18:10 Uhr

Inhaltsverzeichnis:    1. Einführung  -  2. Grafisches Lösungsverfahren  -  3. Übung zum grafischen Lösungsverfahren  -  4. Verschiedene Lösungsmöglichkeiten  -  
5. Memo-Quiz zu verschiedene Lösungsmöglichkeiten  -  6. Eine, keine oder unendlich viele Lösungsmöglichkeiten?

2. Grafisches Lösungsverfahren

Motivation Hatos 3.PNG

Wie du siehst kann man ein lineares Gleichungssystem grafisch lösen.
Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören, in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen.

Versuche nun das folgende lineare Gleichungssystem zu lösen:


( I ) y + 3 = 2x    und    ( II ) y + x = 3


1. Schritt: Zuerst musst du die beiden Gleichungen nach y auflösen, damit du Sie einzeichnen kannst!

Wie lautet die Gleichung ( I ) y + 3 = 2x nach y aufgelöst? (!y= 2x+3) (y= 2x-3) (!y= 1/2x)

Wie lautet die Gleichung ( II ) y + x = 3 nach y aufgelöst? (y= -x+3) (!y= x+3) (!y= -x-3)

2. Schritt: Nun kann man die Geraden in ein Koordinatensystem einzeichnen.

Lernpfad 1 Aufgabe 2 Hatos.png

Die rote Gerade gehört zu folgender Gleichung: (!y = - x + 3) (y = 2x - 3)

Die blaue Gerade gehört zu folgender Gleichung: (y = - x + 3) (!y = 2x - 3)

3. Schritt: Wie lautet der Schnittpunkt der beiden Geraden? (![ 1 | 2 ]) ([ 2 | 1 ]) (![ 3 | 0 ])


4. Schritt: Mache die Probe. Setze die Koordinaten des Schnittpunktes (siehe 3. Schritt) in deine beiden Anfangsgleichungen ein.

Ziehe hierfür mit gehaltener linker Maustaste die richtigen Zahlen in die freien Felder und klicke anschließend auf prüfen!

Gleichung 1:

y + 3 = 2x
     
1 + 3 = 4
     
4 = 4

Diese Aussage ist wahr

Gleichung 2:

y + x = 3
     
1 + 2 = 3
     
3 = 3

Diese Aussage ist wahr

Also lautet die Lösungsmenge dieses linearen Gleichungssystems:

L = {(2/1)}

Motivation Hatos 4.PNG



Lies dir den Merkekasten sorgfältig durch!


Hatos Merke.PNG
Das grafische Lösungsverfahren!


1.Schritt: Löse beide Gleichungen nach y auf, um jeweils die Form y = mx + t zu erhalten.



2.Schritt: Zeichen die Geraden zu den beiden Funktionsgleichungen in ein Koordinatensystem.







3.Schritt: Lies die Koordinaten des Schnittpunkts der beiden Geraden ab.


4.Schritt: Mache die Probe (mit beiden Ausgangsgleichungen) und gib dann die Lösungsmenge an.

Beispiel:

( I ) y + x = 4 und ( II ) 2y = x – 1

( I ) y = -x + 4
( II ) y = ½ x – ½

Grafisch.png


S ( 3 | 1 )


( I ) 1 + 3 = 4 (wahr)
( II ) 2 * 1 = 3 – 1 (wahr)

L = { ( 3 | 1 ) }


→Hier gehts weiter

Hier gehts zurück

Von „http://dmuw.zum.de/index.php?title=Lineare_Gleichungssysteme_grafisch_lösen/Station_2&oldid=17939“