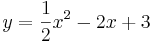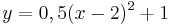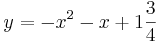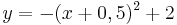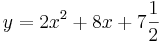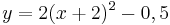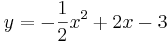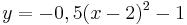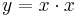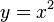Exkurs Quadratische Funktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 1: Zeile 1:
 +
<div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em">
 +
<div style="font-size:100%; line-height:120%; padding: .5em; background-color:#00C5CD; border-bottom:1px solid #aaaaaa;">
 +
[[Bild:Vista-Community Help.png|right|25px]] '''Lernpfad-Navigator'''
 +
</div>
 +
<div style="background:#fff;padding: .5em; padding-bottom: 1em; font-size: 90%;">
 +
 +
*[[Potenzen und Potenzfunktionen]]
 +
**[[Exkurs Lineare Funktionen]]
 +
**[[Exkurs Quadratische Funktionen]]
 +
**[[Potenzfunktionen]]
 +
**[[Potenzfunktionsabbildungen]]
 +
*[[Exponential- & Logarithmusfunktion]]
 +
*[[Trigonometrie]]
 +
*[[Abbildungen im Koordinatensystem]]
 +
</div>
 +
<div style="font-size:90%; padding: .5em; background-color:#00C5CD; border-top:1px solid #aaaaaa;">
 +
[[LERNPFAD]]
 +
</div></div><noinclude>[[Kategorie:Vorlage:Benutzerbausteine|.]]
 +
[[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude>
 +
 +
 
==Quadratische Funktionen==
 
==Quadratische Funktionen==
 
{| border="0"
 
{| border="0"

Version vom 29. Mai 2010, 11:06 Uhr

Vista-Community Help.png
Lernpfad-Navigator

LERNPFAD


Quadratische Funktionen

Arbeitsauftrag

Quadratische Funktionen oder Parabeln hast du in der neunten Klasse kennengelernt. Alle Infos zu Scheitelpunkts- und Normform sind auf den folgenden Folien nochmal zusammengefast - schaus dir an!

{{#slideshare:quadratisch-100520104946-phpapp02}}

Aufgaben

Nun wieder praktisches Arbeiten mit Quadratischen Funktionen.

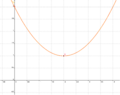
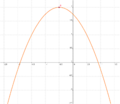
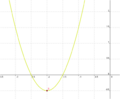
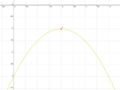
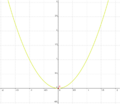
Aufgabe 1 Peter Fischer Papier.png

Ordne den Funktionsgleichungen ihre Graphen zu. Achte auf die Merkmale von Parabeln.

Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu

y=\frac{1}{2}x^2-2x+3 Peter Fischer P1.png y=0,5(x-2)^2+1
y=-x^2-x+1\frac{3}{4} Peter Fischer P2.png y=-(x+0,5)^2+2
y=2x^2+8x+7\frac{1}{2} Peter Fischer P3.png y=2(x+2)^2-0,5
y=-\frac{1}{2}x^2+2x-3 Peter Fischer P4.png y=-0,5(x-2)^2-1
y=x \cdot x Peter Fischer P5.png y=x^2
Aufgabe 2

Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst.

Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Wie kannst du die Parabel y=-\frac{1}{2}x^2+3x+5 zeichnen?

Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen
Den Punkt S(-3/5) einzeichnen und von dort aus die Werte der Parabel y=-\frac{1}{2} abtragen
Drei Werte ausrechnen, einzeichnen und verbinden
Den Scheitel ermitteln (Quadratische Ergänzung!), einzeichnen und von diesem aus die Werte der Parabel y=-\frac{1}{2} abtragen
Die Parabelschablone im Koordinatenursprung nach unten ansetzen und um den Vektor {-3 \choose 5} verschieben>

Punkte: 0 / 0


Aufgabe 3 Peter Fischer Papier.png

Berechnungen zu quadratischen Funktionen

1.

Brechne die Schnittpunkte der ...
Prabeln y=-\frac{1}{2}x^2+3x+5 und y=2x^2+3. S(/); T(/) (2 Nachkommastellen)
Parabel y=-1\frac{1}{2}+3x-\frac{1}{2} mit der Geraden y=-1\frac{1}{2}-3\frac{1}{2} S(/); T(/)
Brechne die Funktionsgleichung der Parabel mit a=-1 und den Punkten A(0,5/-1,5); B(-1/3)
y=

Punkte: 0 / 0


Weiter gehts zu Potenzfunktionen


Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktionsabbildungen
Von „http://dmuw.zum.de/index.php?title=Exkurs_Quadratische_Funktionen&oldid=19392“