Trigonometrie
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! |
[ www.slideshare.net is not an authorized iframe site ]
Potenzfunktion
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Sinus, Kosinus, Tangens
Sinus, Kosinus, Tangens
Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Trigonometrie zusammenfasst. Du kannst es dir auch ausdrucken!
![]() MindMap Potenzen und Potenzfunktionen
MindMap Potenzen und Potenzfunktionen
Leerzeile
Aufgaben
Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!
| Aufgabe 1 Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. |
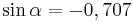 |
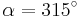 |
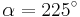
|
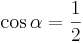 |
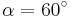 |
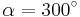
|
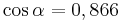 |
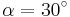 |
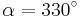
|
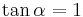 |
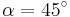 |
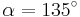
|
Leerzeile
| Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. |
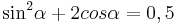
Leerzeile
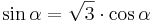
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
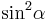 durch
durch 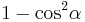 ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.
ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.