Mantelfläche des Zylinders: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Hier werden wir uns nun um die Mantelfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft, Stifte, Geodreieck, eine leere Klopapierrolle ( | + | Hier werden wir uns nun um die Mantelfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft, Stifte, Geodreieck, eine leere Klopapierrolle (diese bekommst du von mir ausgeteilt) und eine Schere. |
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
==1. Aufgabe== | ==1. Aufgabe== | ||
<br> | <br> | ||
| − | Du | + | Du hast eine leere Klopapierrolle von mir bekommen. Mit dieser werden wir nun in der ersten Aufgabe herausfinden, wie wir die Mantelfläche eines Zylinders berechnen können! |
{| {{Prettytable}} | {| {{Prettytable}} | ||
|- style="background-color:#8DB6CD" | |- style="background-color:#8DB6CD" | ||
| Zeile 36: | Zeile 36: | ||
<br> | <br> | ||
Jetzt müssen wir nur noch die Länge und die Breite herausfinden. | Jetzt müssen wir nur noch die Länge und die Breite herausfinden. | ||
| − | Die Breite entspricht unserer Höhe des Zylinders. Die Länge ist so groß wie der Umfang der Grundfläche. Da diese ein Kreis ist, enspricht die Länge der Mantelfläche dem Umfang des Kreises, also <math>l=U=2 | + | Die Breite entspricht unserer Höhe des Zylinders. Die Länge ist so groß wie der Umfang der Grundfläche. Da diese ein Kreis ist, enspricht die Länge der Mantelfläche dem Umfang des Kreises, also <math>l=U=2\cdot r\cdot \pi</math>. |
| − | Also lautet die Formel zur Berechnung der Mantelfläche M=2 | + | Also lautet die Formel zur Berechnung der Mantelfläche <math>M=2\cdot r\cdot \pi\cdot h_K</math>. |
Beschrifte nun die passenen Seiten deiner aufgeschnittenen Klopapierrolle mit den passenden Längen. So sollte das nun aussehen: | Beschrifte nun die passenen Seiten deiner aufgeschnittenen Klopapierrolle mit den passenden Längen. So sollte das nun aussehen: | ||
[[Bild:Klopapierrolle beschriftet.JPG|centre|450px]] | [[Bild:Klopapierrolle beschriftet.JPG|centre|450px]] | ||
| Zeile 45: | Zeile 45: | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{{Merke| | {{Merke| | ||
| − | :Mantelfläche des Zylinders <math>M=2 | + | :Mantelfläche des Zylinders <math>M=2\cdot r\cdot \pi\cdot h_K</math> |
Übertrage diese Formel bitte in dein Schulheft unter der Überschrift "Mantelfläche des Zylinders". | Übertrage diese Formel bitte in dein Schulheft unter der Überschrift "Mantelfläche des Zylinders". | ||
}} | }} | ||
| Zeile 56: | Zeile 56: | ||
:a) Eine zylinderförmige Chipsschachtel hat einen Radius von 4cm und eine Höhe von 30cm. Wie groß ist die Werbefläche, wenn nur die Mantelfläche bedruckt wird? | :a) Eine zylinderförmige Chipsschachtel hat einen Radius von 4cm und eine Höhe von 30cm. Wie groß ist die Werbefläche, wenn nur die Mantelfläche bedruckt wird? | ||
:b) Ein Eishockeypuck hat eine Mantelfläche von 58,09cm². Die Höhe beträgt 2,5cm. Wie groß ist der Radius des Pucks? | :b) Ein Eishockeypuck hat eine Mantelfläche von 58,09cm². Die Höhe beträgt 2,5cm. Wie groß ist der Radius des Pucks? | ||
| − | Hilfe: <span style="background:#000000">r=M | + | Hilfe: <span style="background:#000000"><math>r=\frac {M}{2\cdot hK\cdot \pi}</math></span> |
</div> | </div> | ||
<br> | <br> | ||
| Zeile 65: | Zeile 65: | ||
Jetzt kannst du in folgendem Quiz dein Wissen testen und überprüfen, ob du alles verstanden hast. Die Begründung deiner Antworten schreibst du bitte auf deinen Laufzettel! | Jetzt kannst du in folgendem Quiz dein Wissen testen und überprüfen, ob du alles verstanden hast. Die Begründung deiner Antworten schreibst du bitte auf deinen Laufzettel! | ||
| − | Ist die Formel <math>M=d | + | Ist die Formel <math>M=d\cdot \pi\cdot h_K</math> richtig? (ja) (!nein) |
| − | Kreuze die Zylinder an | + | Kreuze die Zylinder an! ([[Bild:Klopapier.JPG|100px]]) (![[Bild:Zuckerhut.JPG|100px]]) (![[Bild:Glas.JPG|100px]]) ([[Bild:Müsli.JPG|100px]]) |
Was für eine Fläche kann die Mantelfläche des Zylinders sein? (!Parallelogramm) (!Kreis) (Rechteck) (!Raute) (Quadrat) | Was für eine Fläche kann die Mantelfläche des Zylinders sein? (!Parallelogramm) (!Kreis) (Rechteck) (!Raute) (Quadrat) | ||
| − | </div> | + | </div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
<br> | <br> | ||
| Zeile 101: | Zeile 79: | ||
<br> | <br> | ||
Als Hausaufgabe löse bitte die Aufgaben, die ich dir austeile auf einem extra Blatt, das du morgen abgibst. | Als Hausaufgabe löse bitte die Aufgaben, die ich dir austeile auf einem extra Blatt, das du morgen abgibst. | ||
| + | <br> | ||
| + | Weiter geht es mit dem vierten Teil des Lernpfades: [[../Oberfläche des Zylinders|Oberfläche des Zylinders]] | ||
</div> | </div> | ||
Aktuelle Version vom 30. Mai 2010, 10:24 Uhr
Hier werden wir uns nun um die Mantelfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft, Stifte, Geodreieck, eine leere Klopapierrolle (diese bekommst du von mir ausgeteilt) und eine Schere.
1. Aufgabe
Du hast eine leere Klopapierrolle von mir bekommen. Mit dieser werden wir nun in der ersten Aufgabe herausfinden, wie wir die Mantelfläche eines Zylinders berechnen können!
| Schritt 1 | ||
|---|---|---|
 |
Hier siehst du eine ganze Klopapierrolle. Zeichne nun wie auf dem Bild mit deinem Geodreieck eine gerade Linie darauf. |
| Schritt 2 | ||
|---|---|---|
 |
Jetzt musst du die Klopapierrolle an der gezeichneten Linie entlang aufschneiden. |
| Schritt 3 | ||
|---|---|---|
 |
Als nächstes legst du die aufgeschnittene Rolle flach vor dir auf den Tisch. |
Überlege nun, anhand der Fragen, die ich dir nun Stelle, wie man diese Fläche berechnen kann:
Welche Fläche hat unsere Klopapierrolle jetzt? Rechteck
Wie berechnet man die Fläche? Länge mal Breite
Jetzt müssen wir nur noch die Länge und die Breite herausfinden.
Die Breite entspricht unserer Höhe des Zylinders. Die Länge ist so groß wie der Umfang der Grundfläche. Da diese ein Kreis ist, enspricht die Länge der Mantelfläche dem Umfang des Kreises, also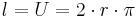 
.
Also lautet die Formel zur Berechnung der Mantelfläche 
.
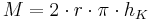Beschrifte nun die passenen Seiten deiner aufgeschnittenen Klopapierrolle mit den passenden Längen. So sollte das nun aussehen:
Somit können wir nun die Mantelfläche des Zylinders berechnen, wenn du noch Fragen hast, kannst du bei den Aufgaben gerne deine Klopapierrolle als Hilfe nehmen.
 Merke
Übertrage diese Formel bitte in dein Schulheft unter der Überschrift "Mantelfläche des Zylinders". |
2. Aufgabe
Löse folgende Aufgaben in deinem Schulheft, schreibe die Ergebnisse aber auch auf deinen Laufzettel!
- a) Eine zylinderförmige Chipsschachtel hat einen Radius von 4cm und eine Höhe von 30cm. Wie groß ist die Werbefläche, wenn nur die Mantelfläche bedruckt wird?
- b) Ein Eishockeypuck hat eine Mantelfläche von 58,09cm². Die Höhe beträgt 2,5cm. Wie groß ist der Radius des Pucks?
Hilfe: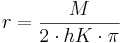 
3. Aufgabe
Jetzt kannst du in folgendem Quiz dein Wissen testen und überprüfen, ob du alles verstanden hast. Die Begründung deiner Antworten schreibst du bitte auf deinen Laufzettel!
Ist die Formel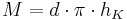 
richtig? (ja) (!nein)
Kreuze die Zylinder an! (
) (!
) (!
) (
)
Was für eine Fläche kann die Mantelfläche des Zylinders sein? (!Parallelogramm) (!Kreis) (Rechteck) (!Raute) (Quadrat)
Nun hast du den zweiten und dritten Teil des Lernpfades geschafft. Gib deinen Laufzettel bei mir ab.
Jetzt bist du fit genug, um in der nächsten Stunde die Oberfläche des neuen Körpers kennenzulernen.
Als Hausaufgabe löse bitte die Aufgaben, die ich dir austeile auf einem extra Blatt, das du morgen abgibst.
Weiter geht es mit dem vierten Teil des Lernpfades: Oberfläche des Zylinders
