Potenzfunktionsabbildungen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 30: | Zeile 30: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | + | So nun noch ein paar Aufgaben zur Abbildung von Potenzfunktionen | |
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="1000" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
| + | Ordne die Bildfunktionen den Ursprungsfunktionen zu. | ||
| + | |} | ||
| + | <div class="zuordnungs-quiz"> | ||
| + | <big>'''Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu'''</big><br> | ||
| + | {| | ||
| + | | <math>f mit y=0,5 \cdot (x+2)^3-1 \vec{v}={-2 \choose 3}</math> || <math>f' mit y=0,5 \cdot (x+4)^3+1</math> | ||
| + | |- | ||
| + | | <math>f mit y=0,5 \cdot (x+2)^3-1 \vec{v}={3 \choose -2}</math>; x-Achse k=3 || <math>f' mit y=1,5 \cdot (x+1)^3-4</math> | ||
| + | |- | ||
| + | | <math>f mit y=1,5 \cdot (x-2)^{-2}-2 \vec{v}={1 \choose -2}</math> || <math>f' mit y=1,5 \cdot (x-3)^3-4</math> | ||
| + | |- | ||
| + | | <math>f mit y=0,5 \cdot (x-2)^{2}-2 \vec{v}={0 \choose 2}</math> || <math>f' mit y=1,5 \cdot 0,5 \cdot (x-2)^2</math> | ||
| + | |} | ||
| + | </div> | ||
Version vom 30. Mai 2010, 22:01 Uhr
Lernpfad-Navigator
Potenzfunktionsabbildungen
| Arbeitsauftrag
Potenzfunktionen können durch Abbildungen verändert werden. Wie die Funktionsgleichung nach einer Abbildung durch Orthogonalter Affinität an der x-Achse und einer Parallelverschiebung aussieht erfährst du hier. |
{{#slideshare:potenzfunktionsabbildungen-100520105117-phpapp02}}
Aufgaben
So nun noch ein paar Aufgaben zur Abbildung von Potenzfunktionen
| Aufgabe 1 Ordne die Bildfunktionen den Ursprungsfunktionen zu. |
Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu
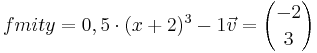 |
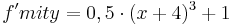
|
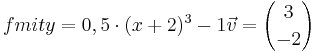 ; x-Achse k=3 ; x-Achse k=3 |
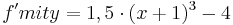
|
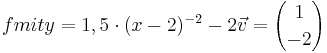 |
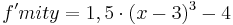
|
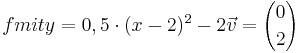 |
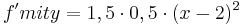
|
Weiter gehts zu Abschnitt II Exponential- & Logarithmusfunktion
Potenzen und Potenzfunktionen

