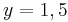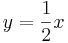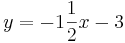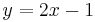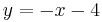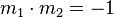Exkurs Lineare Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 45: | Zeile 45: | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{| | {| | ||
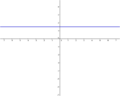
| − | | y=1,5|| [[Bild:Peter Fischer_Y=1,5.png|120px]] | + | | <math>\quad y=1,5</math>|| [[Bild:Peter Fischer_Y=1,5.png|120px]] |
|- | |- | ||
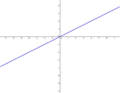
| <math>y=\frac{1}{2}x</math> || [[Bild:Peter_Fischer_Y=0,5x.png|120px]] | | <math>y=\frac{1}{2}x</math> || [[Bild:Peter_Fischer_Y=0,5x.png|120px]] | ||
| Zeile 51: | Zeile 51: | ||
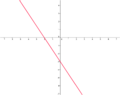
| <math>y=-1\frac{1}{2}x-3</math> ||[[Bild:Peter Fischer_Y=-1,5x-3.png|120px]] | | <math>y=-1\frac{1}{2}x-3</math> ||[[Bild:Peter Fischer_Y=-1,5x-3.png|120px]] | ||
|- | |- | ||
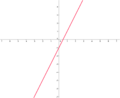
| − | | y=2x-1 || [[Bild:Peter_Fischer_Y=2x-1.png|120px]] | + | | <math>\quad y=2x-1</math> || [[Bild:Peter_Fischer_Y=2x-1.png|120px]] |
|- | |- | ||
| − | | y=-x-4|| [[Bild:Peter Fischer_Y=-x-4.png|120px]] | + | | <math>\quad y=-x-4</math>|| [[Bild:Peter Fischer_Y=-x-4.png|120px]] |
|} | |} | ||
</div> | </div> | ||
| Zeile 70: | Zeile 70: | ||
{| | {| | ||
| − | | Parallele Geraden|| y=0,5x ||<math> y=\frac{1}{2}x-3</math> || <math>y=\frac{4}{2}x+2</math> ||<math> y=0,5x +\sqrt{2}</math> | + | | Parallele Geraden|| <math>\quad y=0,5x</math> ||<math> y=\frac{1}{2}x-3</math> || <math>y=\frac{4}{2}x+2</math> ||<math> y=0,5x +\sqrt{2}</math> |
|- | |- | ||
| − | | Senkrechte Geraden || <math>y=\frac{1}{3}+1</math> || y=3x-4 | + | | Senkrechte Geraden || <math>y=\frac{1}{3}+1</math> || <math>\quad y=3x-4</math> |
|- | |- | ||
| − | | Parallele zur y-Achse || x=3 || x=-4,25 | + | | Parallele zur y-Achse || <math>\quad x=3</math> || <math>\quad x=-4,25</math> |
|- | |- | ||
| − | | Parallele zur x-Achse || y=5 || y=-9 || <math>y=\pi</math> | + | | Parallele zur x-Achse || <math>\quad y=5</math> || <math>\quad y=-9</math> || <math>\quad y=\pi</math> |
|} | |} | ||
</div> | </div> | ||
| Zeile 90: | Zeile 90: | ||
| type="{}" } | | type="{}" } | ||
Berechne den Schnittpunkt der Geraden | Berechne den Schnittpunkt der Geraden | ||
| − | <math>y=\frac{1}{2}x+4</math> und y=-x-5. | + | <math>y=\frac{1}{2}x+4</math> und <math> y=-x-5. \quad S({ -6 _5}/{ 1 _5})</math> |
<popup name="Tipp"> Gleichsetzen der Gleichungen für Schnittpunkte. | <popup name="Tipp"> Gleichsetzen der Gleichungen für Schnittpunkte. | ||
| − | <math>y=\frac{5}{6}x+11\frac{1}{2}</math> und <math>y=\frac{2}{3}x+10 | + | <math>y=\frac{5}{6}x+11\frac{1}{2}</math> und <math>y=\frac{2}{3}x+10. \quad S({ 9 _5}/{ 16 _5})</math> |
| − | Brechne die Funktionsgleichung der Geraden durch die Punkte A(2/3); B(1/-2) | + | Brechne die Funktionsgleichung der Geraden durch die Punkte <math>A(2/3); \quad B(1/-2) y={ x+1 _5} </math> |
| − | + | ||
| − | <popup name="Tipp"> Um m und t berechnen zu können musst du ein Gleichungssystem aufstellen, in dem du A und B in <math>y=mx+t</math> einsetzt! </popup> | + | <popup name="Tipp"> Um m und t berechnen zu können musst du ein Gleichungssystem aufstellen, in dem du A und B in <math>\quad y=mx+t</math> einsetzt! </popup> |
</quiz> | </quiz> | ||
Version vom 1. Juni 2010, 07:48 Uhr
Lernpfad-Navigator
Lineare Funktionen
| Arbeitsauftrag
Geraden kennst du bereits aus der achten Klasse, hier sind nochmal die wichtigsten Eigenschaften zusammengefasst. Klick dich einfach durch! |
{{#slideshare:linear-100526023200-phpapp02}}
Aufgaben
Auch zu linearen Funktionen solltest du nun ein paar Aufgaben erledigen.
| Aufgabe 1
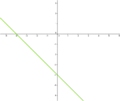
Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's! |
| Aufgabe 2
Sortiere die Funktionsgleichungen nach ihren Eigenschaften in Kategorien. |
| Parallele Geraden | 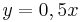 |
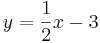 |
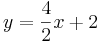 |
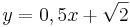
|
| Senkrechte Geraden | 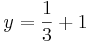 |
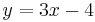
| ||
| Parallele zur y-Achse | 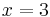 |
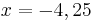
| ||
| Parallele zur x-Achse | 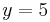 |
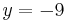 |
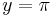
|
| Aufgabe 3 Berechnungen zu linearen Funktionen. |
Weiter gehts zu Exkurs Quadratische Funktionen
Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktionsabbildungen