Exkurs Geometrie: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 12: Zeile 12:
  
 
   
 
   
−
=== Flächeninhaltsberechnungen ===  
+
===Flächeninhaltsberechnungen ===  
 
{| border="1"
 
{| border="1"
 
! width="12" style="background-color:#FFD700;"|
 
! width="12" style="background-color:#FFD700;"|
Zeile 33: Zeile 33:
  
 
====Flächeninhalt von Dreiecken====
 
====Flächeninhalt von Dreiecken====
−
 
−
 
−
 
  
 
{{#slideshare:skalarprodukt-100609154205-phpapp01}}
 
{{#slideshare:skalarprodukt-100609154205-phpapp01}}
  
−
<poem>
 
−
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
 
−
</poem>
 
−
 
−
 
−
==Aufgaben==
 
−
Hier hast du es ebenfalls mit alten Abschlussprüfunen zu tun. Hier sind allerdings Vektoren in Abhängigkeit eines Winkels gegeben. Um Koordinaten oder Winkel zu berechenn solltest du das Skalarprodukt verwenden!
 
  
 +
=== Schrägbilder zeichnen===
 
{| border="1"
 
{| border="1"
 
! width="12" style="background-color:#FFD700;"|
 
! width="12" style="background-color:#FFD700;"|
−
| width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] '''
+
| width="1000" style="text-align:left" style="background-color:#FFEC8B;"|'''Anleitung zum Anfertigen eines Schrägbildes. [[Bild:Peter_Fischer_Idee.png|60px]] '''  
−
--------
+
----------------------
−
Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; B2). 
+
In dem folgenden GeoGebraApplet wird Schritt für Schritt gezeigt wie ein Schrägbild einer Pyramide entsteht, die in der Abschlussprüfung 2006 Aufgabe A 3 zu zeichnen war.
−
------------
+
Du kannst der Anleitung folgen und auf einem Papier zeichnen, dein Ergebnis, dann mit dem am Computer vergleichen oder einfach die Schritte anzeigen und versuchen nachzuvollziehen.
−
Die Pfeile <math>\vec{AB_n}={3 \cdot \cos \varphi -2 \choose 3}</math> und <math>\vec{AC_n}={2 \cdot \cos \varphi -3 \choose {\sin}^2 \varphi}</math> mit <math>\quad A(2|1)</math> spannen für <math>\varphi \in [0^\circ; 180^\circ]</math> Dreiecke <math>\quad AB_nC_n</math> auf.
+
 
|}
 
|}
  
−
{|
+
<poem>
−
|[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']]
+
3.0 Das gleichschenklige Dreieck ABC mit der Basis <math>\quad \overline{BC}=12cm</math> und der Höhe <math>\quad \overline{AD}=9cm</math> ist die Grundfläche der Pyramide ABCS. Die Spitze S liegt senkrecht über dem Mittelpunkt D der Stecke <math>\quad [BC]</math> mit <math>\quad \overline{DS}=8cm</math>.
−
|<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="900" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Gleichschenklig-Rechtwinklig.ggb"/>
+
−
</popup>
+
−
|}
+
  
−
{| border="1"
+
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
−
|Für <math>\quad \varphi =30^\circ</math> ergeben sich die Vektoren <math>\quad \vec{AB_1}</math> und <math>\quad \vec{AC_n}</math>, die einen Winkel mit dem Maß <math>\quad \alpha</math> einschließen. Berechnen sie das Maß <math>\quad \alpha</math> auf 2 Stellen gerundet.
+
−
{|
+
−
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']]
+
−
|<popup name="Lösung">  
+
−
[[Bild:Peter_Fischer_Formelsammlung.png|40px]]
+
−
* <math>\cos \alpha =\frac{\vec{AB_1} \bigodot \vec{AC_1}}{|\vec{AB_1}| \cdot |\vec{AC_1}|}</math>
+
−
* <math>\cos \alpha =\frac{{0,60 \choose 3} \bigodot {-1,27 \choose 0,25}}{\sqrt{0,60^2+3^2} \cdot \sqrt{(-1,27)^2+0,25^2}}</math>
+
−
* <math>\cos \alpha =\frac{0,60 \cdot (-1,27)+3 \cdot 0,25}{\sqrt{0,60^2+3^2} \cdot \sqrt{(-1,27)^2+0,25^2}}</math>
+
−
* <math>\alpha=90,17^\circ</math>  
+
−
</popup>
+
−
|}
+
  
−
<quiz display="simple">
+
3.1 Zeichen Sie ein Schrägbild der Pyramide ABCDS. Dabei soll die Strecke <math>\quad [AD]</math> auf der Schrägbildachse liegen.
−
{
+
Für die Zeichnung: <math>\quad q=\frac{1}{2}; \omega=45^\circ</math>
−
| type="{}" }
+
−
'''Lösung:''' <math>\quad \alpha</math>={ 90,17 _7}° (2 Nachkommastellen)
+
−
</quiz>
+
−
|}
+
  
−
<span style="color:#FFFFFF"><big>Leerzeile</big></span>  
+
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
  
−
{| border="1"
+
<ggb_applet height="600" width="900" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Schrägbild.ggb" />
−
|Berechnen Sie den Wert von <math>\quad \varphi</math>, sodass der Punkt C<sub>4</sub> auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C<sub>4</sub>. (<math>C_n(2\cos \varphi-1|{\sin} \varphi)</math>)
+
−
{|
+
−
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']]
+
−
|<popup name="Tipp">
+
−
Punkte auf der y-Achse besitzen die x-Koordinate 0!
+
−
</popup>
+
−
|}
+
−
<quiz display="simple">
+
−
{
+
−
| type="{}" }
+
−
'''Lösung:''' <math>\varphi</math>={ 60,00 _5}° und C<sub>4</sub>({ 0 _5}|{ 1,75 _5}) (2 Nachkommastelle)
+
−
</quiz>
+
−
|}
+
  
−
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
 
−
 
−
{| border="1"
 
−
|Im rechtwinkligen Dreieck A<sub>5</sub>C<sub>5</sub> ist die Strecke [B<sub>5</sub>C<sub>5</sub>] die Hypothenuse. Berechnen Sie den zugehörigen Wert von <math>\varphi</math>.
 
−
{|
 
−
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']]
 
−
|<popup name="Tipp">
 
−
Rechter Winkel zwischen 2 Vektoren -> Skalarprodukt = 0!
 
−
</popup>
 
−
|}
 
−
<quiz display="simple">
 
−
{
 
−
| type="{}" }
 
−
'''Lösung:''' <math>\varphi</math>={ 30,12 _5}°  (2 Nachkommastelle)
 
−
</quiz>
 
−
|}
 
  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
−
 
+
</poem>
  
 
<poem>
 
<poem>

Version vom 16. Juni 2010, 08:43 Uhr

Inhaltsverzeichnis

Wichtiges zur Geometrie

Bemerkung

Auf dieser Seite sollen Themen zur Geometrie wiederholt werden, die bereits vor der zehnten Klasse bekannt sein sollen und für die Prüfung wichtig sein können|}



Flächeninhaltsberechnungen

Generelles um Flächeninhalte von Figuren zu ermitteln. Peter Fischer Idee.png
  • Flächenformeln
  • Flächenberechnung durch Zerlegung
  • Flächeninhalt von Dreiecken


Flächenformeln

Im laufe deiner Schulzeit hast du für verschiedene Figuren Flächenformeln kennengelernt, wie 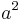\quad a^2 für das Quadrat, 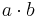\quad a \cdot b für der Rechteck oder 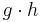\quad g \cdot h für das Parallelogramm. Eine Übersicht dieser Formeln findest du auf dem MindMap "Figuren und ihre Eigenschaften". Wenn du alle Angaben hast, um diese Formeln zu benutzen ist alles gut.


Flächenberechnung durch Zerlegung

Falls dir Angaben fehlen oder es keine Formel für diese Figur existiert, so kannst du versuchen sie in einfachere Figuren zu Zerlegen. Häufig hilft es Figuren in Dreiecke zu zerlegen, da für Dreiecke mehrere Formeln zur Verfügung stehen.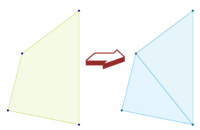Peter Fischer Zerlegung.png


Flächeninhalt von Dreiecken

{{#slideshare:skalarprodukt-100609154205-phpapp01}}


Schrägbilder zeichnen

Anleitung zum Anfertigen eines Schrägbildes. Peter Fischer Idee.png

In dem folgenden GeoGebraApplet wird Schritt für Schritt gezeigt wie ein Schrägbild einer Pyramide entsteht, die in der Abschlussprüfung 2006 Aufgabe A 3 zu zeichnen war. Du kannst der Anleitung folgen und auf einem Papier zeichnen, dein Ergebnis, dann mit dem am Computer vergleichen oder einfach die Schritte anzeigen und versuchen nachzuvollziehen.

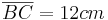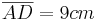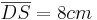3.0 Das gleichschenklige Dreieck ABC mit der Basis \quad \overline{BC}=12cm und der Höhe \quad \overline{AD}=9cm ist die Grundfläche der Pyramide ABCS. Die Spitze S liegt senkrecht über dem Mittelpunkt D der Stecke \quad [BC] mit \quad \overline{DS}=8cm.

Leerzeile

3.1 Zeichen Sie ein Schrägbild der Pyramide ABCDS. Dabei soll die Strecke \quad [AD] auf der Schrägbildachse liegen.
Für die Zeichnung: 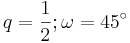\quad q=\frac{1}{2}; \omega=45^\circ

Leerzeile




Leerzeile

Weiter gehts zu Abschnitt IV Abbildungen im Koordinatensystem
Leerzeile

Trigonometrie
LERNPFAD | Trigonometrie | Trigonometrische Funktionen | Berechnungen in Dreiecken | Skalarprodukt | Exkurs: Wichtiges zur Geometrie
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Prüfungsvorbereitung/Trigonometrie/Exkurs_Geometrie&oldid=20626“