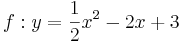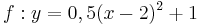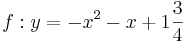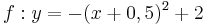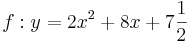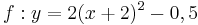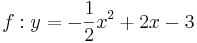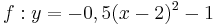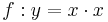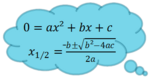Exkurs Quadratische Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: {{#slideshare:quadratisch-100520104946-phpapp02}} <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Parabeln.ggb" />) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> | |
| + | <div style="font-size:100%; line-height:120%; padding: .5em; background-color:#00C5CD; border-bottom:1px solid #aaaaaa;"> | ||
| + | [[Bild:Vista-Community Help.png|right|25px]] '''Lernpfad-Navigator''' | ||
| + | </div> | ||
| + | <div style="background:#fff;padding: .5em; padding-bottom: 1em; font-size: 90%;"> | ||
| − | <ggb_applet height=" | + | *[[Potenzen und Potenzfunktionen]] |
| + | **[[Exkurs Lineare Funktionen]] | ||
| + | **[[Exkurs Quadratische Funktionen]] | ||
| + | **[[Potenzfunktionen]] | ||
| + | **[[Potenzfunktionsabbildungen]] | ||
| + | *[[Exponential- & Logarithmusfunktion]] | ||
| + | *[[Trigonometrie]] | ||
| + | *[[Abbildungen im Koordinatensystem]] | ||
| + | *[[Prüfungsaufgaben]] | ||
| + | </div> | ||
| + | <div style="font-size:90%; padding: .5em; background-color:#00C5CD; border-top:1px solid #aaaaaa;"> | ||
| + | [[LERNPFAD]] | ||
| + | </div></div><noinclude>[[Kategorie:Vorlage:Benutzerbausteine|.]] | ||
| + | [[Kategorie:Vorlage:Navigationsblöcke|Erste Hilfe]]</noinclude> | ||
| + | |||
| + | |||
| + | ==Quadratische Funktionen== | ||
| + | {| border="0" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="1000" style="text-align:left"| '''Arbeitsauftrag''' | ||
| + | -------- | ||
| + | Quadratische Funktionen oder Parabeln hast du in der neunten Klasse kennengelernt. Alle Infos zu Scheitelpunkts- und Normform sind auf den folgenden Folien nochmal zusammengefast - schaus dir an! | ||
| + | |} | ||
| + | <poem> | ||
| + | {{#slideshare:quadratisch-100609143847-phpapp02}} | ||
| + | |||
| + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| + | {{pdf|Peter Fischer_Quadratisch.pdf|Quadratische Funktionen}} | ||
| + | |||
| + | |||
| + | <ggb_applet height="550" width="750" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Parabeln.ggb" /> | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | </poem> | ||
| + | |||
| + | ==Aufgaben== | ||
| + | Nun wieder praktisches Arbeiten mit Quadratischen Funktionen. | ||
| + | |||
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
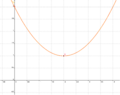
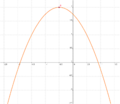
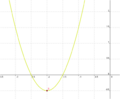
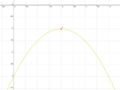
| + | Ordne den Funktionsgleichungen ihre Graphen zu. Achte auf die Merkmale von Parabeln. | ||
| + | |} | ||
| + | <div class="zuordnungs-quiz"> | ||
| + | <big>'''Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu'''</big><br> | ||
| + | {| | ||
| + | | <math>\quad f: y=\frac{1}{2}x^2-2x+3</math> || [[Bild:Peter Fischer_P1.png|120px]] || <math>\quad f: y=0,5(x-2)^2+1</math> | ||
| + | |- | ||
| + | | <math>\quad f: y=-x^2-x+1\frac{3}{4}</math> || [[Bild:Peter Fischer_P2.png|120px]] || <math>\quad f: y=-(x+0,5)^2+2</math> | ||
| + | |- | ||
| + | | <math>\quad f: y=2x^2+8x+7\frac{1}{2}</math> ||[[Bild:Peter Fischer_P3.png|120px]] || <math>\quad f: y=2(x+2)^2-0,5</math> | ||
| + | |- | ||
| + | | <math>\quad f: y=-\frac{1}{2}x^2+2x-3</math> || [[Bild:Peter Fischer_P4.png|120px]] || <math>\quad f: y=-0,5(x-2)^2-1</math> | ||
| + | |- | ||
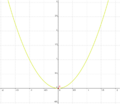
| + | | <math>\quad f: y=x \cdot x</math> || [[Bild:Peter Fischer_P5.png|120px]] || <math>\quad f: y=x^2 </math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 2''' | ||
| + | -------- | ||
| + | Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { Wie kannst du die Parabel <math>y=-\frac{1}{2}x^2+3x+5</math> zeichnen? } | ||
| + | + Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen | ||
| + | - Den Punkt S(-3/5) einzeichnen und von dort aus die Werte der Parabel <math>y=-\frac{1}{2}</math> abtragen | ||
| + | - Drei Werte ausrechnen, einzeichnen und verbinden | ||
| + | + Den Scheitel ermitteln (Quadratische Ergänzung!), einzeichnen und von diesem aus die Werte der Parabel <math>y=-\frac{1}{2}</math> abtragen | ||
| + | - Die Parabelschablone im Koordinatenursprung nach unten ansetzen und um den Vektor <math>{-3 \choose 5}</math> verschieben | ||
| + | </quiz> | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 3 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
| + | Berechnungen zu quadratischen Funktionen | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Brechne die Schnittpunkte der ... | ||
| + | Prabeln <math>y=-\frac{1}{2}x^2+3x+5</math> und <math>y=2x^2+3</math>. S({ 1 _5}/{ 5 _5}); T({ -1.80 _5}/{ 9.48 _5}) (2 Nachkommastellen) | ||
| + | </quiz> | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | Gleichsetzen der Gleichungen für Schnittpunkte; Quadratische Gleichungen mit der allg. Lösungsformel berechnen. [[Bild:Peter_Fischer_Lösungsformel.png|150px]] | ||
| + | </popup> | ||
| + | |} | ||
| + | |||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Parabel <math>y=-1\frac{1}{2}+3x-\frac{1}{2}</math> mit der Geraden <math>y=-1\frac{1}{2}-3\frac{1}{2}</math> S({ -2 _5}/{ -0,5 _5}); T({ -1 _5}/{ -2 _5}) | ||
| + | </quiz> | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Brechne die Funktionsgleichung der Parabel mit a=-1 und den Punkten A(0.5/-1.5); B(-1/3) | ||
| + | y={ -2x²-4x+1 } | ||
| + | </quiz> | ||
| + | |||
| + | '''Weiter gehts zu [[Potenzfunktionen]]''' | ||
| + | |||
| + | |||
| + | <div style="background:#00BFFF;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | ||
| + | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid #00BFFF; background-color:#f6fcfe;"> | ||
| + | [[LERNPFAD]] | [[Potenzen und Potenzfunktionen]] | [[Exkurs Lineare Funktionen]] | [[Exkurs Quadratische Funktionen]] | [[Potenzfunktionen]] | [[Potenzfunktionsabbildungen]] </div><noinclude> | ||
Version vom 16. August 2010, 10:05 Uhr
Lernpfad-Navigator
Quadratische Funktionen
| Arbeitsauftrag
Quadratische Funktionen oder Parabeln hast du in der neunten Klasse kennengelernt. Alle Infos zu Scheitelpunkts- und Normform sind auf den folgenden Folien nochmal zusammengefast - schaus dir an! |
{{#slideshare:quadratisch-100609143847-phpapp02}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Quadratische Funktionen
Quadratische Funktionen
Leerzeile
Aufgaben
Nun wieder praktisches Arbeiten mit Quadratischen Funktionen.
| Aufgabe 1 Ordne den Funktionsgleichungen ihre Graphen zu. Achte auf die Merkmale von Parabeln. |
Leerzeile
| Aufgabe 2
Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. |
Leerzeile
| Aufgabe 3 Berechnungen zu quadratischen Funktionen |
Leerzeile
Weiter gehts zu Potenzfunktionen
Potenzen und Potenzfunktionen