Abbildungen im Koordinatensystem: Unterschied zwischen den Versionen
| (28 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Abbildungen im Koordinatensystem1}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==Abbildungen im Koordinatensystem - Parallelverschiebung== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ==Abbildungen im Koordinatensystem== | + | |
{| border="0" | {| border="0" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| − | | width=" | + | | width="900" style="text-align:left"| '''Arbeitsauftrag''' |
-------- | -------- | ||
| − | + | Hier geht es nicht um die Eigenschaften der Abbildungen, die solltest du schon eine Weile kennen und kannst sie auch in der Formelsammlung nachschlagen. | |
| + | Stattdessen solltest du Bildpunkte mit Hilfe von Abbildungsmatrizen berechnen können. Die Rechnung mit Matrizen wird nochmal erklärt, anschließend wird die Parallelverschiebung als erste Abbildung verdeutlicht. | ||
|} | |} | ||
| − | |||
| − | |||
<poem> | <poem> | ||
| − | <ggb_applet height=" | + | {{#slideshare:parallelverschiebung-100609155245-phpapp01}} |
| + | |||
| + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| + | {{pdf|Peter Fischer_Parallelverschiebung.pdf|Parallelverschiebung}} | ||
| + | |||
| + | Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Abbildungen im Koordinatensystem zusammenfasst. Du kannst es dir auch ausdrucken! | ||
| + | {{pdf|Peter Fischer_Abbildungen.pdf|MindMap Abbildungen}} | ||
| + | |||
| + | |||
| + | Das folgende GeoGebra-Applet zeigt dir zur Wiederholung eine Parallelverschiebung, deren Verschiebungsvektor du verändern kannst. | ||
| + | <ggb_applet height="550" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Parallelverschiebung.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 36: | Zeile 27: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | + | Bei der Parallelverschiebung, ebenso wie bei der orthogonalen Affinität spielt die Abbildungsmatrix eine geringere Rolle, stattdessen werden ganze Funktionen abgebildet, wie bereits in Potenzfunktionsabbildungen beschrieben. | |
| + | Im folgenden wartet eine ehemalige Prüfungsaufgabe auf dich. | ||
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| − | | width=" | + | | width="900" style="text-align:left" style="background-color:#FFBBFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | + | Abbilden einer Exponentialfunktion. (Abschlussprüfung 2006; Wahlteil ; A1 (verändert)). | |
| + | ------------ | ||
| + | Gegeben ist die Funktion f mit der Gleichung <math>\quad y=1,5^{x+3}+1.</math> | ||
|} | |} | ||
| − | |||
| − | {| | + | {| |
| − | + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | |
| − | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="550" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Exponentialaufgabe.ggb"/> | |
| − | + | </popup> | |
| − | + | |} | |
| − | + | ||
| − | + | {| border="1" | |
| − | + | |Der Graph der Funktion f wird durch orthogonale Affinität mit der x-Achse als Affinitätsachse und dem Affinitätsmaßstab <math>\quad k=-2</math> und anschließender Parallelverschiebung mit <math>\vec{v}={2 \choose 10}</math> auf den Graphen zu f' abgebildet. | |
| − | + | {| | |
| − | + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |
| − | + | |<popup name="Tipp"> | |
| + | *Wird eine Funktion durch Orthogonale Affinität abgebildet, so wird der Funktoinsterm mit k multipliziert | ||
| + | *Wird eine Funktion parallelverschoben mit dem Vektor <math>\vec{v}={v_x \choose v_y}</math>, so gilt: <math>\quad x'=x-v_x </math> und <math>\quad v_y </math> wird zu dem Funktionsterm addiert. (siehe auch Potenzfunktionsabbildungen) | ||
| + | </popup> | ||
| + | |} | ||
| + | |||
| + | |||
| + | <quiz display="simple"> | ||
| + | { Wähle aus welche Gleichung f ' beschreibt:} | ||
| + | - <math>\quad y=2 \cdot 1,5^{x+1}+8</math> | ||
| + | - <math>\quad y=-2 \cdot 1,5^{x-1}-8</math> | ||
| + | + <math>\quad y=-2 \cdot 1,5^{x+1}+8</math> | ||
| + | </quiz> | ||
|} | |} | ||
| − | |||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 64: | Zeile 68: | ||
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| − | | width=" | + | | width="900" style="text-align:left" style="background-color:#FFBBFF;"| '''Aufgabe 2 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | Hier | + | Abbilden einer Logarithmusfunktion. (Abschlussprüfung 2008; Wahlteil ; A1). |
| + | ------------ | ||
| + | Gegeben ist die Funktion f mit der Gleichung <math>\quad y=\log_3{(x+1)}-2</math>. | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | ||
| + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="550" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Logarithmusaufgabe.ggb"/> | ||
| + | </popup> | ||
| + | |} | ||
| + | |||
| + | {| border="1" | ||
| + | |Geben Sie die Definitionsmenge der Funktion f, sowie die Gleichung der Asymptote h an. | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | [[Bild:Peter_Fischer_Formelsammlung.png|40px]] In der Formelsammlung stehen Eigenschaften zu Funktionen und deren Definitionsmengen und Asympoten. | ||
| + | </popup> | ||
|} | |} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | { | + | { |
| type="{}" } | | type="{}" } | ||
| − | <math>\quad | + | Lösung: <math>\quad \mathbb{D}=\{x|x></math>{ -1 _5}<math>\quad \}</math> |
| − | + | Asymptote h: { x=-1 _5} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</quiz> | </quiz> | ||
| + | |} | ||
| + | {| border="1" | ||
| + | |Der Graph der Funktion f wird durch Parallelverschiebung mit dem Vektor <math>\vec{v}={a \choose 4}</math> mit <math>\quad a \in \mathbb{R}</math> auf den Graphen f' abgebildet. Der Punkt <math>\quad P'(0|4)</math> liegt auf dem Graphen zu f'. | ||
| + | Brechnen Sie den Wert von a. | ||
| + | Ermitteln Sie sodann die Gleichung der Funktion f' durch Rechnung. | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | [[Bild:Peter_Fischer_Formelsammlung.png|40px]] | ||
| + | Entweder verschiebst du f mit dem Vektor <math>\vec{v}={a \choose 4}</math> und setzt P' in die erhaltene Gleichung ein oder du bildest die Punkte <math>\quad P_n(x|\log_3{(x+1)}-2</math> mit der Abbildungsgleichung ab und setzt <math>\quad x=0</math> ein. | ||
| + | </popup> | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: a= { -2 _5} | ||
| + | Bildfunktion f': { 2 _3}<math>\cdot \log_3</math> ({ x+3 _7}) { +2 _3} | ||
| + | </quiz> | ||
| + | |} | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Weiter gehts zu [[ | + | '''Weiter gehts zu [[/Abbildung durch Drehung|Abbildung durch Drehung]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 90: | Zeile 126: | ||
<div style="background:#D15FEE;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | <div style="background:#D15FEE;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Abbildungen im Koordinatensystem]] | [[Abbildung durch Drehung]] | [[Abbildung durch Achsenspiegelung]] | [[Weitere Abbildungen | + | [[../|LERNPFAD]] | [[../Abbildungen im Koordinatensystem|Abbildungen im Koordinatensystem]] | [[/Abbildung durch Drehung|Abbildung durch Drehung]] | [[/Abbildung durch Achsenspiegelung|Abbildung durch Achsenspiegelung]] | [[/Weitere Abbildungen|Weitere Abbildungen]] </div> |
| + | |||
| + | |||
| + | |||
| + | [[zum-wiki:Mathematik-digital/Figuren im Koordinatensystem]] | ||
Aktuelle Version vom 15. Oktober 2011, 12:04 Uhr
Abbildungen im Koordinatensystem - Parallelverschiebung
| Arbeitsauftrag
Hier geht es nicht um die Eigenschaften der Abbildungen, die solltest du schon eine Weile kennen und kannst sie auch in der Formelsammlung nachschlagen. Stattdessen solltest du Bildpunkte mit Hilfe von Abbildungsmatrizen berechnen können. Die Rechnung mit Matrizen wird nochmal erklärt, anschließend wird die Parallelverschiebung als erste Abbildung verdeutlicht. |
{{#slideshare:parallelverschiebung-100609155245-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Parallelverschiebung
Parallelverschiebung
Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Abbildungen im Koordinatensystem zusammenfasst. Du kannst es dir auch ausdrucken!
![]() MindMap Abbildungen
MindMap Abbildungen
Das folgende GeoGebra-Applet zeigt dir zur Wiederholung eine Parallelverschiebung, deren Verschiebungsvektor du verändern kannst.
Leerzeile
Aufgaben
Bei der Parallelverschiebung, ebenso wie bei der orthogonalen Affinität spielt die Abbildungsmatrix eine geringere Rolle, stattdessen werden ganze Funktionen abgebildet, wie bereits in Potenzfunktionsabbildungen beschrieben. Im folgenden wartet eine ehemalige Prüfungsaufgabe auf dich.
| Aufgabe 1 Abbilden einer Exponentialfunktion. (Abschlussprüfung 2006; Wahlteil ; A1 (verändert)). Gegeben ist die Funktion f mit der Gleichung |
Der Graph der Funktion f wird durch orthogonale Affinität mit der x-Achse als Affinitätsachse und dem Affinitätsmaßstab 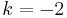 und anschließender Parallelverschiebung mit und anschließender Parallelverschiebung mit 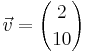 auf den Graphen zu f' abgebildet. auf den Graphen zu f' abgebildet.
|
Leerzeile
| Aufgabe 2 Abbilden einer Logarithmusfunktion. (Abschlussprüfung 2008; Wahlteil ; A1). Gegeben ist die Funktion f mit der Gleichung |
| Geben Sie die Definitionsmenge der Funktion f, sowie die Gleichung der Asymptote h an.
|
Leerzeile
Weiter gehts zu Abbildung durch Drehung
Leerzeile
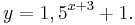
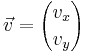 , so gilt:
, so gilt: 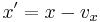 und
und 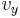 wird zu dem Funktionsterm addiert. (siehe auch Potenzfunktionsabbildungen)
wird zu dem Funktionsterm addiert. (siehe auch Potenzfunktionsabbildungen)
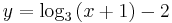 .
.
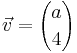 mit
mit 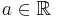 auf den Graphen f' abgebildet. Der Punkt
auf den Graphen f' abgebildet. Der Punkt 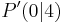 liegt auf dem Graphen zu f'.
liegt auf dem Graphen zu f'.
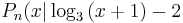 mit der Abbildungsgleichung ab und setzt
mit der Abbildungsgleichung ab und setzt 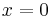 ein.
ein.

