Übung zur Zerlegungsgleichheit: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Seite verschoben)
 
(linkfix)
 
(4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 56: Zeile 56:
 
{|
 
{|
 
*'''''<span style="color: red">[BD]</span> ist die Diagonale.'''''  
 
*'''''<span style="color: red">[BD]</span> ist die Diagonale.'''''  
−
*'''''<span style="color: red">[FK]</span> eine Parallele zur Seite [BC] und <span style="color: red">[LM]</span> eine Parallele zu [AB] '''''
+
*'''''<span style="color: red">[FK]</span> eine Parallele zur Seite [DC] und <span style="color: red">[LM]</span> eine Parallele zu [AD] '''''
 
* ''''' <span style="color: red">Sie schneiden sich im Punkt S</span>'''''
 
* ''''' <span style="color: red">Sie schneiden sich im Punkt S</span>'''''
 
[[Bild:Ebert_MotivatorRot.jpg|100px]] '''" Die Parallelogramme SLAF und MCKS besitzen den gleichen Flächeninhalt!"'''<br>  
 
[[Bild:Ebert_MotivatorRot.jpg|100px]] '''" Die Parallelogramme SLAF und MCKS besitzen den gleichen Flächeninhalt!"'''<br>  
−
| <ggb_applet height="300" width="700"  showResetIcon="true" filename="Ebert_Gnomon.ggb" /> ||'''''Hat Nils Recht?'''''
+
| <ggb_applet height="300" width="700"  showResetIcon="true" filename="Ebert_Gnomonneu.ggb" /> ||'''''Hat Nils Recht?'''''
 
:'''''Du kannst <span style="color: red">S</span> variieren. Beobachte, wie sich Teilfiguren ändern.'''''
 
:'''''Du kannst <span style="color: red">S</span> variieren. Beobachte, wie sich Teilfiguren ändern.'''''
−
<quiz display="simple">
 
−
{'''Welches Parallelogramm halbiert die Diagonale?'''}
 
−
+Das Parallelogramm '''ABCD'''
 
−
-Das Parallelogramm '''SMCK'''
 
−
+Das Parallelogramm '''SFDM'''
 
−
-Das Parallelogramm '''ADML'''
 
−
+Das Parallelogramm '''LSKB'''
 
  
 +
 +
<div class="schuettel-quiz">
 +
*Die Diagonale '''halbiert''' das Parallelogramm ABCD.
 +
</div>
 +
 +
<quiz display="simple">
 
{ '''Welche Dreiecke sind kongruent zueinander?''' }
 
{ '''Welche Dreiecke sind kongruent zueinander?''' }
−
+Dreieck '''BCD''' und Dreieck '''BAD'''
+
+Dreieck '''BDC''' und Dreieck '''BAD'''
 
-Dreieck '''<span style="color: blue ">SKB</span>''' und Dreieck '''BAD'''
 
-Dreieck '''<span style="color: blue ">SKB</span>''' und Dreieck '''BAD'''
−
-Dreieck '''<span style="color: orange">DMS</span>''' und Dreieck '''<span style="color: green">SLB</span>'''
+
-Dreieck '''<span style="color: #EEEE00 ">DMS</span>''' und Dreieck '''<span style="color: green">SBL</span>'''
−
+Dreieck '''<span style="color: orange">DMS</span>''' und Dreieck '''<span style="color: red">BFS</span>'''
+
+Dreieck '''<span style="color: #EEEE00 ">DMS</span>''' und Dreieck '''<span style="color: orange ">DSF</span>'''
−
+Dreieck '''<span style="color: blue">SKB</span>''' und Dreieck '''<span style="color: green">SLB</span>'''
+
+Dreieck '''<span style="color: blue">SKB</span>''' und Dreieck '''<span style="color: green">SBL</span>'''
  
 
</quiz>
 
</quiz>
Zeile 82: Zeile 81:
  
 
Dreieck DMS und '''DFS''' sind kongruent zueinander. <br>
 
Dreieck DMS und '''DFS''' sind kongruent zueinander. <br>
−
Ebenso Dreieck '''SKB''' und SLB. <br>  
+
Ebenso Dreieck '''SKB''' und SBL. <br>  
−
Entfernt man diese Dreiecke von den kongruenten Dreiecken  BAD und BCD, so  
+
Entfernt man diese Dreiecke von den kongruenten Dreiecken  BAD und BDC, so  
 
<br> haben die Restfiguren '''SLAF''' und SMCK den gleichen Flächeninhalt.
 
<br> haben die Restfiguren '''SLAF''' und SMCK den gleichen Flächeninhalt.
 
</div>
 
</div>
Zeile 115: Zeile 114:
 
<br>
 
<br>
  
−
'''Hier geht es zurück zur''' [[ Zusammenfassung zur Zerlegungsgleichheit]]
+
'''Hier geht es zurück zur''' [[../Zusammenfassung zur Zerlegungsgleichheit/]]

Aktuelle Version vom 28. Dezember 2011, 14:11 Uhr


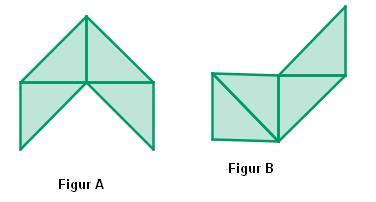
Aufgabe 1 zum Aufwärmen

Begründe, warum die folgenden Figuren A und B den gleichen Flächeninhalt besitzen:

Ebert ZerlegungsgleichheitAufgabe1neu.jpg

Hier siehst Du Majas Lösung. Ist sie richtig?

Figur A und B sind zueinander zerlegungsgleich. Sie bestehen aus je 4 zueinander kongruenten Teildreiecken. Damit besitzen sie den gleichen Flächeninhalt.




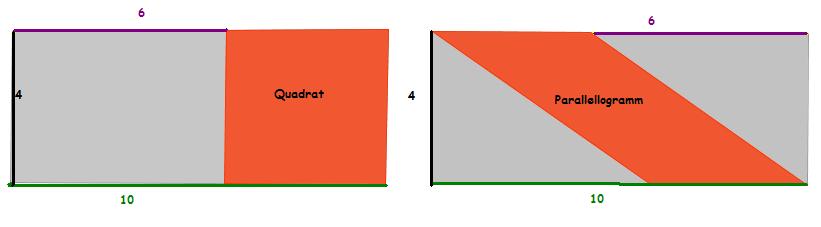
Aufgabe 2 für Geübte: Ergänzungsgleiche Figuren

Zwei Rechtecken mit der Länge 10cm und der Breite 4cm ist ein Quadrat und ein Parallelogramm einbeschrieben.
Was haben Quadrat und Parallelogramm gemeinsam?
Ebert Scherungsaufgabe.jpg

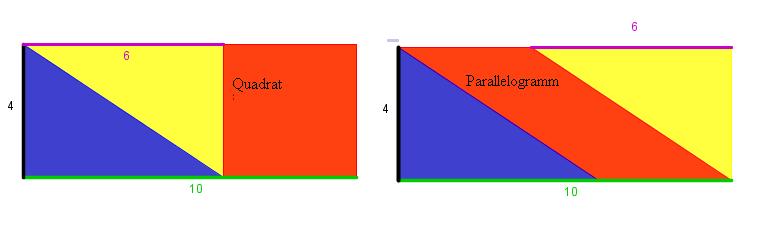
Tipp:

Überlege, wie man das linke und das rechte Rechteck geeignet zerlegen kann.


Beantworte dazu die Fragen:

1. Haben Quadrat und Parallelogramm den gleichen Umfang?

ja
nein

2. Sind Quadrat und Parallelogramm ergänzungsgleiche Figuren?

ja
nein

3. Besitzen Quadrat und Parallelogramm den gleichen Flächeninhalt?

ja
nein

4. Sind Quadrat und Parallelogramm zerlegungsgleich?

nein
ja

Punkte: 0 / 0


Ebert MotivatorRot.jpg

Bist Du ganz sicher, dass Du den Hinweis von Nils brauchst?

Ebert QuadratundParallelogramm.jpg



Aufgabe 3 für Profis: Wunderliche Parallelogramme

  • [BD] ist die Diagonale.
  • [FK] eine Parallele zur Seite [DC] und [LM] eine Parallele zu [AD]
  • Sie schneiden sich im Punkt S
Ebert MotivatorRot.jpg" Die Parallelogramme SLAF und MCKS besitzen den gleichen Flächeninhalt!"
 Hat Nils Recht?
Du kannst S variieren. Beobachte, wie sich Teilfiguren ändern.


  • Die Diagonale halbiert das Parallelogramm ABCD.

1. Welche Dreiecke sind kongruent zueinander?

Dreieck BDC und Dreieck BAD
Dreieck SKB und Dreieck BAD
Dreieck DMS und Dreieck SBL
Dreieck DMS und Dreieck DSF
Dreieck SKB und Dreieck SBL

Punkte: 0 / 0

Dreieck DMS und DFS sind kongruent zueinander.
Ebenso Dreieck SKB und SBL.
Entfernt man diese Dreiecke von den kongruenten Dreiecken BAD und BDC, so
haben die Restfiguren SLAF und SMCK den gleichen Flächeninhalt.





1. Die Parallelogramme SLAF und SMCK besitzen den gleichen Flächeninhalt

ja
nein

Punkte: 0 / 0

Ebert Loballgemein.jpg


Get more and explore:

Ebert Lob1.jpg

Gratuliere, Du hast den 1. Lernpfad erfolgreich bearbeitet!
Du kennst Dich jetzt schon sehr gut mit zerlegungsgleichen Figuren aus und bist fit die Flächeninhaltsformel von Figuren zu entdecken.

Nils und Maja begleiten dich dabei wieder:


→Hier geht es weiter zum 2. Lernpfad

Hier geht es zurück zur Zusammenfassung zur Zerlegungsgleichheit

Von „http://dmuw.zum.de/index.php?title=Zerlegungsgleichheit_von_Figuren/Übung_zur_Zerlegungsgleichheit&oldid=30708“