Parameter a: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
(40 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
= Der Parameter a =
+
<div style="margin:0; margin-right:4px; margin-left:0px; border:1px solid  #6C7B8B; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
 +
[[Variationen/Quadratische Funktionen1| Beginn]] -  &nbsp; [[Variationen/Quadratische Funktionen1/Einstieg|Fußball-WM]] - [[Variationen/Quadratische Funktionen1/Halbzeit|Die Halbzeitpause]] - [[Variationen/Quadratische Funktionen1/Funktionen|Rückblick]] - [[Variationen/Quadratische Funktionen1/Quadratische Funktionen|Video]] - [[Variationen/Quadratische Funktionen1/Parameter a |Der Parameter a]] - [[Variationen/Quadratische Funktionen1/Parameter c1|Aufgaben zu a]] - [[Variationen/Quadratische Funktionen1/Parameter c|Der Parameter c]] - [[Variationen/Quadratische Funktionen1/Parameter c2 |Aufgaben zu c]] - [[Variationen/Quadratische Funktionen1/Parameter b | Kleine Entspannung]] - [[Variationen/Quadratische Funktionen1/Parameter b1|Die Normalform]] - [[Variationen/Quadratische Funktionen1/Scheitelpunktform |Die Scheitelpunktsform]] - [[Variationen/Quadratische Funktionen1/übungen zur Scheitelpunktform |Übungen zur Scheitelspunktform]] - [[Variationen/Quadratische Funktionen1/übungen zur Scheitelpunktform2|weitere Übungen]] - [[Variationen/Quadratische Funktionen1/Von Scheitelpunktsform zur Normalform  |zur Normalform]] - [[Variationen/Quadratische Funktionen1/zurück zur ersten Parabel |zurück zur Anfangsparabel]]</div><noinclude>[[Kategorie:Vorlage:Navigationsleisten]]</noinclude>
  
  
−
Nachdem du jetzt f(x)=x<sup>2</sup> schon kennst erweitern wir das ein bisschen.
+
<div style="border: 2px solid #E0EEEE ; background-color:#E0EEEE; padding:12px;">
−
Man kann so eine quadratische Funktion auch durch die Formel f(x)=ax<sup>2</sup> ausdrücken.
+
 
−
Für welches a erhält man dan wohl die Normalparabel als Graph?
+
 
 +
= Der Parameter a =
 +
 
 +
<div style="border: 2px solid white; background-color:white; padding:7px;">
 +
Nachdem du jetzt f(x)=x<sup>2</sup> schon kennst, erweitern wir das ein bisschen.
 +
Man kann eine quadratische Funktion auch durch die Formel f(x)=ax<sup>2</sup> ausdrücken.
 +
Für welches a erhält man dann wohl die Normalparabel als Graph?
 +
</div>
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
 
Man erhält eine Normalparabel, wenn a = ''' 1(Zahl eintragen) ''' ist.
 
Man erhält eine Normalparabel, wenn a = ''' 1(Zahl eintragen) ''' ist.
Zeile 10: Zeile 18:
 
<br/>  
 
<br/>  
  
−
 
+
<div style="border: 2px solid white; background-color:white; padding:7px;">
−
Finde in der nächsten Aufgabe selber heraus, was a bei einer Parabel bewirkt.
+
Finde in der nächsten Aufgabe heraus, was a bei einer Parabel bewirkt.
−
                                                  ;Aufgabe
+
</div>
 +
;                                                     Aufgabe 6
 
{|border="0" cellspacing="0" cellpadding="4"
 
{|border="0" cellspacing="0" cellpadding="4"
 
|align = "left" width="450"|
 
|align = "left" width="450"|
Zeile 21: Zeile 30:
 
|valign="top"|  
 
|valign="top"|  
 
<br/>
 
<br/>
−
 
+
Verschiebe den Schieberegler, um zu schauen, was sich mit '''a''' ändert.
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
  
−
Für a gleich eins erhältst du die '''Normalparabel'''. Ist a > 1 (a größer als eins) so ist die Parabel '''enger''' als die Normalparabel.Ist 0 < a < 1 (a ist größer als 0 aber kleiner als 1), so ist die Parabel  '''weiter''' als die Normalparabel. Ist a  < 0 '''Europa''' dagegen auf der '''nördlichen'''.
+
Für a gleich eins erhältst du die '''Normalparabel'''. Ist a > 1,  so ist die Parabel <br/> '''enger''' als die Normalparabel. Ist 0 < a < 1 , so ist die Parabel  '''weiter''' als die Normalparabel. Ist a  < 0 , so ist die Parabel nach '''unten''' geöffnet.
 +
 
 +
</div>
 +
|}
 +
;Aufgabe 7
 +
<div class="zuordnungs-quiz">
 +
<big>'''Zuordnung'''</big><br>
 +
Ordne den Funktionen den jeweils richtigen Graph zu und den Graphen die richtigen Funktionen.
 +
{|
 +
| [[Bild:-0,5x2.png|150px]] || f(x)= -0,5x<sup>2</sup>
 +
|-
 +
| [[Bild:-x2.png|150px]] || f(x)= -x<sup>2</sup>
 +
|-
 +
| [[Bild:3x2.png|150px]] || f(x)= 3x<sup>2</sup>
 +
|-
 +
| [[Bild:X2.png|150px]] || f(x)= x<sup>2</sup>
 +
|}
 +
</div>
 +
<br/>
 +
 
 +
 
 +
<div style="border: 2px solid white; background-color:white; padding:7px;">
 +
;Aufgabe 8
 +
 
 +
Bist du dir bei dieser Aufgabe nicht sicher, probiere noch einmal den Schieberegler von '''Aufgabe 6'''.
 +
<quiz display="simple">
 +
{ Klicke an, was auf den Graph der jeweiligen Funktion zutrifft. Es stimmen immer zwei Eigenschaften.
 +
| typ="[]" }
 +
| a) Nach oben geöffnet | b) Nach unten geöffnet  | c) Weiter als Normalparabel  | d) Enger als Normalparabel
 +
-+-+ ... f(x)= -7x<sup>2</sup>
 +
+--+ ... f(x)= 4,5x<sup>2</sup>
 +
+-+- ... f(x)= 0,3x<sup>2</sup>
 +
-++- ... f(x)= -0,7x<sup>2</sup>
 +
</quiz>
 +
<br/>
 +
{|border="0" cellspacing="0" cellpadding="4"
 +
|align = "left" width="450"|
 +
[[Bild:Symbollaufzettel.bmp|100px]]
 +
|width=20px|
 +
|valign="top"|
 +
 
 +
[[Datei:Smileyman6.png |link= Variationen/Quadratische Funktionen1/Parameter c1 ]]
 +
|}
 +
__NOCACHE__
  
 
</div>
 
</div>

Aktuelle Version vom 20. Februar 2019, 18:57 Uhr

Beginn -   Fußball-WM - Die Halbzeitpause - Rückblick - Video - Der Parameter a - Aufgaben zu a - Der Parameter c - Aufgaben zu c - Kleine Entspannung - Die Normalform - Die Scheitelpunktsform - Übungen zur Scheitelspunktform - weitere Übungen - zur Normalform - zurück zur Anfangsparabel



Der Parameter a

Nachdem du jetzt f(x)=x2 schon kennst, erweitern wir das ein bisschen. Man kann eine quadratische Funktion auch durch die Formel f(x)=ax2 ausdrücken. Für welches a erhält man dann wohl die Normalparabel als Graph?

Man erhält eine Normalparabel, wenn a = 1(Zahl eintragen) ist.


Finde in der nächsten Aufgabe heraus, was a bei einer Parabel bewirkt.

Aufgabe 6


Verschiebe den Schieberegler, um zu schauen, was sich mit a ändert.

Für a gleich eins erhältst du die Normalparabel. Ist a > 1, so ist die Parabel
enger als die Normalparabel. Ist 0 < a < 1 , so ist die Parabel weiter als die Normalparabel. Ist a < 0 , so ist die Parabel nach unten geöffnet.

Aufgabe 7

Zuordnung
Ordne den Funktionen den jeweils richtigen Graph zu und den Graphen die richtigen Funktionen.

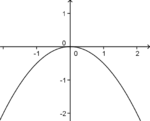-0,5x2.png f(x)= -0,5x2
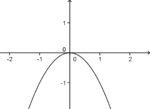-x2.png f(x)= -x2
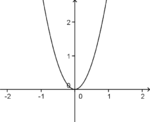3x2.png f(x)= 3x2
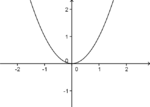X2.png f(x)= x2



Aufgabe 8

Bist du dir bei dieser Aufgabe nicht sicher, probiere noch einmal den Schieberegler von Aufgabe 6.

1. Klicke an, was auf den Graph der jeweiligen Funktion zutrifft. Es stimmen immer zwei Eigenschaften.

a) Nach oben geöffnet b) Nach unten geöffnet c) Weiter als Normalparabel d) Enger als Normalparabel
... f(x)= -7x2
... f(x)= 4,5x2
... f(x)= 0,3x2
... f(x)= -0,7x2

Punkte: 0 / 0


Symbollaufzettel.bmp

Smileyman6.png


Von „http://dmuw.zum.de/index.php?title=Variationen/Quadratische_Funktionen1/Parameter_a&oldid=32143“