Lineare Gleichungssysteme grafisch lösen/Station 4: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | '''Inhaltsverzeichnis:''' [[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|1. Einführung]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|2. Grafisches Lösungsverfahren]] - [[Lineare Gleichungssysteme grafisch lösen/Station 3|3. Übung zum grafischen Lösungsverfahren]] - [[Lineare Gleichungssysteme grafisch lösen/Station 4|4. Verschiedene Lösungsmöglichkeiten]] - [[Lineare Gleichungssysteme grafisch lösen/Station 5|5. Memo-Quiz zu verschiedene Lösungsmöglichkeiten]] - [[Lineare Gleichungssysteme grafisch lösen/Station 6|6. Eine, keine oder unendlich viele Lösungsmöglichkeiten?]] | + | '''Inhaltsverzeichnis:''' [[Benutzer:Sarah Hatos/Lineare Gleichungssysteme grafisch lösen|1. Einführung]] - [[Lineare Gleichungssysteme grafisch lösen/Station 2|2. Grafisches Lösungsverfahren]] - [[Lineare Gleichungssysteme grafisch lösen/Station 3|3. Übung zum grafischen Lösungsverfahren]] - [[Lineare Gleichungssysteme grafisch lösen/Station 4|4. Verschiedene Lösungsmöglichkeiten]] - <br> |
| + | [[Lineare Gleichungssysteme grafisch lösen/Station 5|5. Memo-Quiz zu verschiedene Lösungsmöglichkeiten]] - [[Lineare Gleichungssysteme grafisch lösen/Station 6|6. Eine, keine oder unendlich viele Lösungsmöglichkeiten?]] | ||
</div> | </div> | ||
| Zeile 21: | Zeile 22: | ||
{ Können die Geraden einen Schnittpunkt haben? } | { Können die Geraden einen Schnittpunkt haben? } | ||
| − | + | + Ja | |
| − | + | - Nein | |
{ Kannst du die Geraden so verändern, dass Sie keinen Schnittpunkt haben. } | { Kannst du die Geraden so verändern, dass Sie keinen Schnittpunkt haben. } | ||
| Zeile 47: | Zeile 48: | ||
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| − | '''In den folgenden Zeichungen sind verschiedene | + | '''In den folgenden Zeichungen sind verschiedene lineare Gleichungssyteme grafisch dargestellt.'''<br> |
'''Versuche die nebenstehenden Lückentexte auszufüllen.'''<br> | '''Versuche die nebenstehenden Lückentexte auszufüllen.'''<br> | ||
'''Was fällt dir auf?''' | '''Was fällt dir auf?''' | ||
| Zeile 92: | Zeile 93: | ||
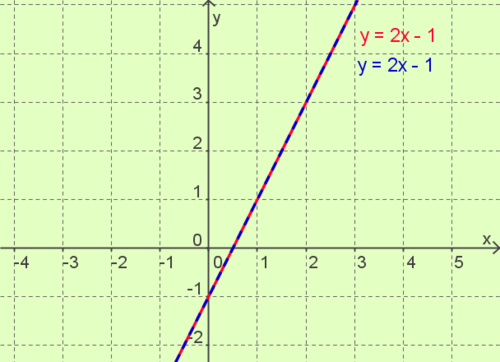
Ihre Steigung und ihre y - Achsenabschnitte sind '''gleich'''.<br> | Ihre Steigung und ihre y - Achsenabschnitte sind '''gleich'''.<br> | ||
Die Lösungsmenge des Beispiels lautet L = { ( x | y ) / y = 2x - 1 }.<br> | Die Lösungsmenge des Beispiels lautet L = { ( x | y ) / y = 2x - 1 }.<br> | ||
| − | Also sind alle Zahlenpaare, die auf diesen Geraden liegen, Lösungen des | + | Also sind alle Zahlenpaare, die auf diesen Geraden liegen, Lösungen des linearen Gleichungssystems. |
</div> | </div> | ||
| Zeile 101: | Zeile 102: | ||
'''Versuche nun die folgende Frage zu beantworten!''' [[Bild:Motivation_Hatos_6.PNG|350px]] | '''Versuche nun die folgende Frage zu beantworten!''' [[Bild:Motivation_Hatos_6.PNG|350px]] | ||
| − | '''Welche Fälle können auftreten?''' (Das | + | '''Welche Fälle können auftreten?''' (Das lineare Gleichungssystem ist eindeutig lösbar, d.h. eine Lösung) (Das lineare Gleichungssystem ist unerfüllbar, d.h. keine Lösung) (Das lineare Gleichungssystem hat unendlich viele Lösungen) (!Das lineare Gleichungssystem hat 2 Lösungen) |
</div> | </div> | ||
| Zeile 110: | Zeile 111: | ||
| − | '''<big>→ [[Lineare Gleichungssysteme grafisch lösen/Station 5| | + | '''<big>→ [[Lineare Gleichungssysteme grafisch lösen/Station 5|Hier gehts weiter]]</big>''' |
| − | [[Lineare Gleichungssysteme grafisch lösen/Station 3|Hier gehts zurück | + | [[Lineare Gleichungssysteme grafisch lösen/Station 3|Hier gehts zurück]] |
Aktuelle Version vom 17. März 2010, 20:18 Uhr
Inhaltsverzeichnis: 1. Einführung - 2. Grafisches Lösungsverfahren - 3. Übung zum grafischen Lösungsverfahren - 4. Verschiedene Lösungsmöglichkeiten -
5. Memo-Quiz zu verschiedene Lösungsmöglichkeiten - 6. Eine, keine oder unendlich viele Lösungsmöglichkeiten?
4. Verschiedene Lösungsmöglichkeiten
Hier sind wieder zwei Geraden f (x) und g (x) dargestellt.
Mit den Schiebereglern kannst du die Steigung ( m ) und den y- Achsenabschnitt ( t ) der Geraden verändern.
Beantworte die Fragen durch Ausprobieren im obigen Koordinatensystem!
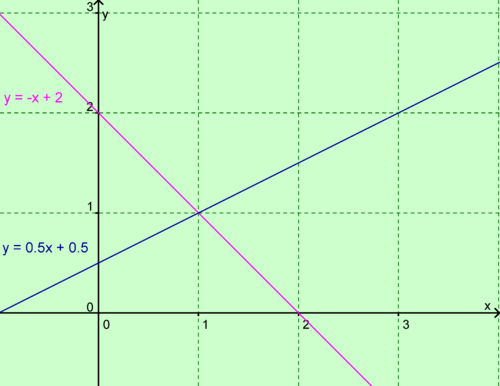
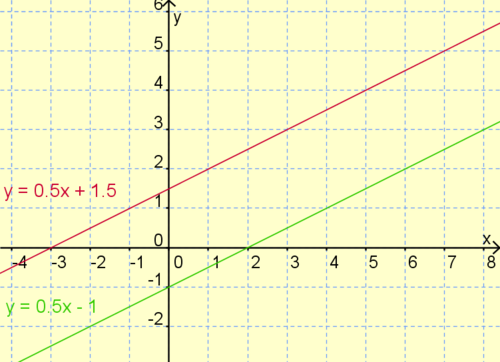
In den folgenden Zeichungen sind verschiedene lineare Gleichungssyteme grafisch dargestellt.
Versuche die nebenstehenden Lückentexte auszufüllen.
Was fällt dir auf?
 |
Die Geraden haben einen Schnittpunkt. |
 |
Die Geraden haben keinen Schnittpunkt. |
 |
Die Geraden sind identisch. |
Versuche nun die folgende Frage zu beantworten! 
Welche Fälle können auftreten? (Das lineare Gleichungssystem ist eindeutig lösbar, d.h. eine Lösung) (Das lineare Gleichungssystem ist unerfüllbar, d.h. keine Lösung) (Das lineare Gleichungssystem hat unendlich viele Lösungen) (!Das lineare Gleichungssystem hat 2 Lösungen)
