Eigenschaften: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(link geändert)
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[Benutzer:Stefan_Baumgart|Übersicht]] - [[Benutzer:Stefan_Baumgart/Einleitung|Einleitung]] - [[Benutzer:Stefan_Baumgart/Zinseszins|Zinseszins]] - [[Benutzer:Stefan_Baumgart/Untersuchung|Untersuchung der Exponentialfunktion]] - [[Benutzer:Stefan_Baumgart/Eigenschaften|Eigenschaften der Exponentialfunktion]] - [[Benutzer:Stefan_Baumgart/Umkehrfunktion|Umkehrfunktion]] - [[Benutzer:Stefan_Baumgart/Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion|Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion]] - [[Benutzer:Stefan_Baumgart/Übungen|Übungen und Lösung des Arbeitsblattes]]
+
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[Lernpfade/Exponential- und Logarithmusfunktion|Übersicht]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Einleitung|Einleitung]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Zinseszins|Zinseszins]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Untersuchung|Untersuchung der Exponentialfunktion]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Eigenschaften|Eigenschaften der Exponentialfunktion]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Umkehrfunktion|Umkehrfunktion]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Rechnerische Beziehung|Rechnerische Beziehung]] - [[Lernpfade/Exponential- und Logarithmusfunktion/Übungen|Übungen und Lösung des Arbeitsblattes]]
 
</div>
 
</div>
 
<br>
 
<br>
Zeile 31: Zeile 31:
  
  
−
→ [[Benutzer:Stefan_Baumgart/Umkehrfunktion|Hier geht´s zur Umkehrfunktion]]
+
→ [[Lernpfade/Exponential- und Logarithmusfunktion/Umkehrfunktion|Hier geht´s zur Umkehrfunktion]]

Aktuelle Version vom 28. Januar 2010, 11:30 Uhr

Übersicht - Einleitung - Zinseszins - Untersuchung der Exponentialfunktion - Eigenschaften der Exponentialfunktion - Umkehrfunktion - Rechnerische Beziehung - Übungen und Lösung des Arbeitsblattes


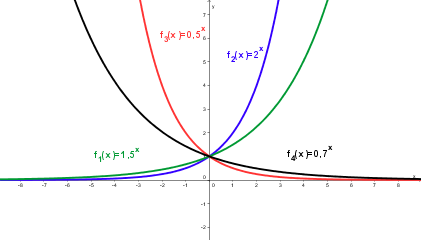
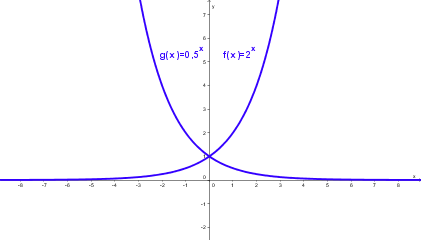
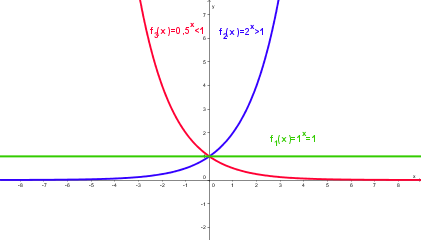
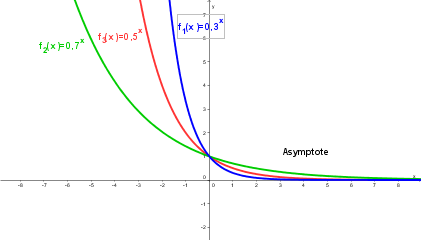
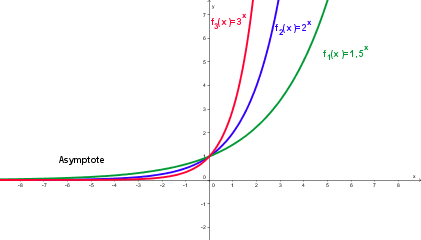
Eigenschaften der Exponentialfunktion

Die Definitionsmenge aller Exponentialfunktionen ist R. Es treten nur positve Funktionswerte auf. Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1). Exponentialfunktionen.png
Exponentialfunktion7.png Die Graphen von f(x) = ax und g(x) = a-x = 1/ax liegen symmetrisch bezüglich der y-Achse.
Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. Exponentialfunktion2.png
Exponentialfunktion6.png Für 0 < a < 1 ist die positive x-Achse Asymptote.
Für a > 1 ist die negative x-Achse Asymptote. Exponentialfunktion5.png


Maehnrot.jpg
Merke:
  • Die Definitionsmenge aller Exponentialfunktionen ist R.
  • Es treten nur positive Funktionswerte auf.
  • Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1).
  • Die Graphen von f(x) = ax und g(x) = a-x = 1/ax liegen symmetrisch bezüglich der y-Achse.
  • Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend.
  • für 0 < a < 1 ist die positive x-Achse Asymptote.
  • Für a > 1 ist die negative x-Achse Asymptote. 


Löse an dieser Stelle das Arbeitsblatt zum Lernpfad


→ Hier geht´s zur Umkehrfunktion

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Exponential-_und_Logarithmusfunktion/Eigenschaften&oldid=14398“