Quadratische Funktionen: Unterschied zwischen den Versionen
(→Aufgabe x) |
(→Quadratische Funktionen und Klippenspringen: Quellcode eingegeben) |
||
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[ | + | __NOTOC__ |
| − | + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[../Einstieg|1. Fußball-WM 2006 - Wasserverbrauch]] | [[../Quadratische Funktionen|2. Quadratische Funktionen und Klippenspringen]] | [[../Übungen zu a|3. Übungen]] | [[../Quadratische Funktionen und der Parameter c|4. Quadratische Funktionen und Volleyball]] | [[../Quadratische Funktionen und der Parameter b|5. Quadratische Funktionen und Fußball]] | [[../Quadratische Funktionen und die Scheitelform|6. Quadratische Funktionen und Basketball]] | [[../Endspurt|7. Endspurt]] | |
| + | </div> | ||
| + | <br\> | ||
| − | =Quadratische Funktionen= | + | ==Quadratische Funktionen und Klippenspringen== |
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| Zeile 10: | Zeile 12: | ||
Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | ||
| − | {{ | + | {| border="0" cellpadding="5" cellspacing="2" style="border: 1px solid {{{Rand|#ca1321}}}; background-color: {{{Hintergrund|#ffffff}}}; border-left: 5px solid {{{RandLinks|#ca1321}}}; margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: {{{Breite|100%}}}" |
| + | |- | ||
| + | | <div style="float:right; margin:0px; margin-top:5px">[[Bild:Maehnrot.jpg|100px]]</div> | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Merke:</div> | ||
| + | |||
| + | Die Graphen von Funktionen mit der Funktionsgleichung '''f(x)=x²''' heißen '''Parabeln'''. | ||
| + | |||
| + | Sie lassen sich auch in der Form '''y=x²''' darstellen. | ||
Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | ||
| − | } | + | |} |
| + | |||
<br /> | <br /> | ||
| − | Schön, nun wissen wir, dass wir es mit Parabeln zu tun haben. Diese sind jedoch nicht immer in der starren Form f(x)=x² dargestellt. In der folgenden Aufgabe kannst du diese Parabel durch | + | Schön, nun wissen wir, dass wir es mit Parabeln zu tun haben. Diese sind jedoch nicht immer in der starren Form f(x)=x² dargestellt. In der folgenden Aufgabe kannst du diese Parabel durch Schieben des Punktes auf dem Schieberegler [[Bild:Schieberegler.bmp]] verändern. |
Aber sieh dir das selbst mal an. | Aber sieh dir das selbst mal an. | ||
| Zeile 33: | Zeile 43: | ||
<ggb_applet width="300" height="550" version="3.2" ggbBase64="UEsDBBQACAAIAD20UzwAAAAAAAAAAAAAAAAvAAAAOThlODE1ZTBhMmJjYTk5YTQxNWZhYzgzYzQ3YWQzMWNcS2xpcHBlLW5ldS5qcGecuGc4XF/497vHYBC9JIPR6yCim1EH0XuLGj+MEoIYnWhD1IzRayZIdEJCRIkkiC5atGiJTvQe0Z/8n+uUN+fFOefeb/a1173XWp/r3uv6fu99M3WzANDqaGhrACAiAAD9u4CbWUANICMlhZCSkEEgEHJyMgpKRirKW7comekZaBjZWDjY2VhgME5eUQFObhEeGExQFi4iJi4lJcUhgFRESCiISkpJ/M8kIHJycspblFAqKqgEF4xL4v9z3LQBdGQgI5AdGMQNENGBwHSgm06A498+SUD/O4D/I0BEYGISUggZOcWtfwkfaAEiEBhMRAwmISEm/jca9m8cIKYjoecSVyFlMHaAcGMYJbCpr8h4VGvbmUy+7/NKOvpEkVPcvgNlZuHjFxCEC0lJy8gikHJq99U1NLW0dUzNzB9YWFpZo52cXVwfubn7+vkHBAYFh0Q/i4mNi09ITEvPyMzKzsnNe11UXFJaVl5RWfe+/kNDY1Pzx68dnV3dPb19/aNj4xOTP6amZxaXlldW19Z/b2weHB4dn/w5/Xt2/j9cIAAM+j/j/5GL7h8XETExmBjyP1wgosD/SaAjJuESJ6VXMYY4YBi4JbBkjKqpr2rbyXkkTfaZHH2+U9zmlVrkO/gftP9N9v8OLOr/F9n/BfZ/c80AlGDQv+KB6QBlYLrOpfEjv35aDYBifaXoe276tnpSWGWt//XCu4s3mgLV5Czd34Sw7DDN1awVAOlhxsDzLRRGP1AZcKePuCB0Xz20xyb/T1Zt+FfLLK0/37BZfUYAzJ/D1nTXxMpz1ilWmv4e758ehDToa4xfDI+5UdnIkflK09feUULDdkd0pESYoIWHPl1Yioq3DfXWaSPBiWbL2P0ebyA5zLOWz8gsps9hHGv06yFf0rPsNFqmhOe7u8MNyuwfGAPXnJ6L2kEZVpYjw5I8GU8lMxtIPyfV9ymk8TKfqbKXXT7W1Q9m9jGKNIOxN+/9tZAnG6yLH+mUzbJX1Pe00RSazVXTFCLpJwqEI/ZsdPqYH/uMv7uf97muhwHELelBbJ+KWz9aKnzu/UMUgYZpVUN7FHDLZ2MCLWk2LWhWAlXnM1uPXvC52WmdYrNzg/M9udf0UzxgBcKVOytRp0Tfum0Cn+h/j1/DOYTS539VzevK5lQ+I+kIfj5f2LNlorUDM2m2bBeyGVC0ACPO0dLPRWbztUcNnJMCFiKqFZHnOKexxCa7Xm3+ACMekgQB7PxMdfQXBnov0b9Cvj1s7yJYEk14myS4n0GhPYarehIKFQLZotbKH1vcPvgJUzUliKaW5Inz9hPhoiTxRcr9dSXvE3WtBLD8uO4FBZMTI02o4ll10JPTttDfRYK70I9/dnpvABoV03YW296tzLnisPakG2DFfLRKkE4Q/sjHgQzJJAPFDvrJnoeaBj+lFPtYI6EBDjOsdupz42uJSfU25JmzeKXzuqJhXWppwUwo0Mn/pFhc0rydWbHSPG7mIw8pGp5BPzWRUU8VpaFVVUHzrqLzaXBbtTnDHUs8WefjSCF7wZ4P9wwCCr5+MPueXt41W2CtH3n6ZCj57y0KI3IYvdCZsaiHQsnwg8vfh59vhfst1ITIrsFVv222ZprclzHN7+NbxQr8eq2vqMkaVE1UdwwyXNZOCDqTUKonmLK8uA8nw9ljDLohqvo6soGAiYT2JSdHd7Uw7TQ7zWd+5LrUpf5P4NKNaMDwJ7SUC2BvLeFI3tBNUFlVKT7rMSsmop1ewJ4wLrayWRwWdzTuG3+4AZpR1OwukhnK2JJvf6YTkx/jLktfZMPsr80oc7K3GZSt9ZrYGK+lb58pKus8IfQHQ5R1HHzCOtktTop8IwLPzNiDd6vPTCcdQ0gvy8E+UnRzn9KUc1nfTTf5FJ8Mf1D82UACNXhK0Z+0ih+PFeFFiMyPnZRdVS6oN6sFO3h7AxtTLH8rTMNo3phKBwb3rQoxtFaAL88f8NcG1T7kewZef3a5a6B6yl124dxv0yfU1/Q6Pdo2tkLyqqR6EX0KeSm2kiZP4/VYR+rtXe0KRSm2ms2diBfC6qRi4Wh8ab3Hz22/8monU77O5Fbi5dEqN2uL4SdC2ChyMBuk2s+tVCjGdXHqsivO/Tfh9edxx4xGZ91HMkAZ9WCBGLYduf1Yb6abDC97ixwmKCDN+CY+tKl/BQ5OTBK9DbVNes75sGmTyumErVv+efDzcqMXOssVl+4fJhbz7lNO290h7wYq6wwGBiSj84N2jG2+JvuEVJim1PlxjobQzv7245rueJPDiUPXqLAJiz6Mkk4KiKYFKM0zstRY+UHfnIihlV3mZWSJXQltP0fjtb3MdxO48A8a6dMCiJDHFVaOJMW8bwdo+iXT58aKDe+q7nJF+5DcHR8YSZNrZN5JDETDVR578hI5+2uTXcMiv5bVO7u9pzWUdZkcMgQrFIRPmHwVaMzXqq0nizTfJFvO8y9CtOROYI5gF6Zn8WOZDqnF+gMbOPvE6nCqnmxO4wxUMX65tkr/9uQduia+Ji9xw8NxjdDaw/wmNvjom4rhXDoT2EFtYsWgXoXJXMcqbb+S6a/CI8Tb10WI8cQMQ/ZK7wDnTPamCjGa0coEKgWlp5N/xJqVABhGBzgpl3Uyfb83GdnMZW3gBj5KDNiFx+vJNsDDnxy6yf4p+bmnh1LLjxwN7ahm7d3TWFJOjAR+FY7ukvf2Fs9hxk0k75VJdWqvLfioSw72hF9JavEeD4ouGDy9ggPb65+5Zqezj4qiR2hKBe3F+6OUMihRQUPw2ezaUoLr7qiX8UTIhRHXRUb+p1FnQ4xxNEfhZYW2KkSKMl0QOciacVo+NEQd/jr5Z8FSIblP/nwmaxGPgpmS9Q0QOhp83xtaUE0kBVXn8QzHKXnJjUvW2xmb8+7AiII2NnTh5vIykjLe2jCQeUkCOmNJSVM5JjRKc9w2Fq5m3aIveB+OA0Vp79huBxx28nrQCadBz30n672cfwoOMYKTihKd0iRsz5ycXIl/3GfK7PVaq0kSu+9MkhnoYevfLXct7f44tyxJTTJ9JJN4zO8CQ7FnUhROkW5xe8txW+IVZ+iUor7TrxImNS1t/wfKoh2p5lmkWZMG1IdTx+175+Z/C259yxJISZTQKrPpvj/affGnAYbpOVtKd6zNmCzRMFYTg66cMP61vzAfuko0EK+nxFiwTF9+Tei72x1UvjzPSjXwKoewo3Qiy5TGuqpg8yzGLABMoEiaGImiXiZUsAnN3id2I1AytCMFfpUdGgkOLclRy5k95CpW3XwIhm+N57/O5ErC0pN2k4ob3L1Dl8Ck824RD1m2IXdmBKS/qw4EA5dFZeASszyV8ZVdxhcnKJT/mZVhWbUuWr5Fk2N68We7FzVm/p8yDcc/I/W7rYP9lKZkuAfDDnJrr35ozKl00Uplq+1tXz+bmJb2tkmeWLW5qyH8GKWqoIK/NlQ8Mp5RD/Rxvu/GXDuBvFSs/BHPH6U7G4CDsz+YkMe08Werj+fdOuO2pVE0hG6qS7OJxozHhvGYXAh7NmROAQEfnD9UiSq5rDg5WTjwv3rK+kmk2YQUSq0Zsrabb1iPFCI1QLHFuR/XbXzL7Vzs7vKZK+XGzB8xtjhBqvU/vx8xTVCakt7ON/6P/rivjEYSG23qOlYNJ346wg3T7ikRlEDnZafIGYG6HxHdK5Ci7SnRfVmILpH1HgYXuNtrBEZrCvxQ3NTfms9DKJYTiRUnEqWFFAyV9ihbExHWE4nVj6iPiwLkxmOCdwbZrXjwGUC097q/fDjEHRXX6i5DJAj65WLgjSih/twlhtXF/hYEdZZikktk3dMMIuQMMw6idci8urHxZuzwEsSCj5Bqf+tVyMNeTYE84Fn2cfHZBRGJfuaQb55R0BkmuZpIllu8M4D1UfEDE63QrOGaiBL0ps9rr5YUXvHKlPii1taQ32lL3WJY0r0C4o/rUFjB2MmbewxzM/PaDpSsZl1iwZY3AMW/t0JD7w2EKTQg4WYGd0ie48SHfScb06QEs1cRM2SOSltXQn+noZJFwoUzzWwYPJVhgG5QWFGiH81awh1kN8R9YrDWumMnmtiKBQJifJ/02ffXe/87uQ+sqqstz1q7K4OYvk+7G2/eXvPoa56wYAvYgVayJHViyvVbzPbvlGq9GXNH/UHOakm7WeWoIJ248NuHwibCd33CatDCTaHVh8dMT3U+N6K5RB6oInjYWmDjDTM103wxVmrw5Tm6vDK4EtbJ+CGHSdN/83RH7LKI9QL3KpmUfS+nFC/cM6Gn62MzDdQliGdNxK/fUXVjrE7v7HGKtJHOYXpWjb/x73aO3mYFBg9tX9nr1MVeFIec+1XVcu9bxZ9pSPim490Jcs+DebeJNHnfC+ENdQzrwUJVyJ20YO6CupbxQI1Psg8mezBAFq8X+fiVe+b4RkCpJi9wAwgOuvSP6lRiqVezFfYplj5w1rndHZp66T33ZaxX2Q7eJFj4eUDfAO2aNMJEipItOG3imc0z0RstZzaZYnry8MMduCcr21eVD5k2vK6w60yF21pluD21dqVM4xCKbpciSVvbnkwAG11vRtfC12nCr625YzOq7kn8XSFeiyey6LOLGl0il7fjXVatAZXzfaHx+nfVFRUYxmH/i8aUFpiMmPjZpPM4ldcy5/FucHXvPRZ9qdoYM7wl8fJstdPPT8lA6pK5qjdNa8mT6PIJM5y4scELwT3IW+uHVxu5KxjdFBpOinPioKjsdtLs4NNLt+IrpaYini9UYozNio/mnrLo939acczQyt04N6UtEEfCvmeBEUsv/kRCscMeJrnYduACg7K89fT72r1qIoch1GWFwur86VMjogSN8JN7+bk80nSC0yQqpR7JPO77IUeohC8jLc28pp8uV3aZjF8nYRVwISxo1WeHu0oZbZ+8UJtuSiPPsE2O5VfZpQJPulNmZGRyIW+lQIX8evtu9zd9e88fPJleNQi8t65iFdm/zJ3C4qjyI/AfC6m3sKCut3LcUVlCqQCXvnje0/fzR8UQ9ky1wZw/52PP6rA4Xy31Oh/xGWzbwoG5Xt09OyrBLJXx5Q096ryDxccB8RFvZsdvAOqQyQfpj9LcTbUDzFNSdGq35iJ0xr7MO9NmeXhlR7aEgRQjwOYit5jw/rjwG0D0Fq34bElonD5N6aZupb5Hl71gt3jfdM/o64+pPI1+Ubf9ZqPzMfmlryfsnRou9Hp91zy+tqrtnU1UPb6PH1y897l/l5fg+pZxTJsk9tGhdF5lZW18DUW+0F1vXX85/gmc0KqKQ/qeyfSslBYby7y3Z9nAN89q8TKa97sRoprG3T4qlxsy6U2Wq8sf8gejs21PFqtUtW9b2MQPPBZTiEIqVhnY2Ng4gZaSHp47gK7cHPCjJAHO99KClveXCuqZEhnsVr/fNoKY0PlO5mW9ytIU3aW4AQJTj5nKXT+YueDnQnFi2ielfKMxPjqMjgFHiQaGhduu8S5pghMq3OKntYlP/oTNFCnYCwtTnvLXx3xX5tVujoMaF6waSzWm63HiBYCCgiAKb8nevkFpAQcrYiOtQe5vYJ4V+lH79TmKF547v4zkNRnoaocN20yXG3K0P2oakcvHc72/ZpL4WHxAKTNCOg6OFBI1x1Vb6X+e6iBqS3pTxMzk3p6ltYIQmd0P/i03Jt2Eq+N5zZ1lu64YXOY22esgsieB9JDjzreAsctPlL4RvsPCnWPsxcqDcblmD9sSDcqZ3blD8VoYtyCjZJoS8fIRq67bPVe3rg7oN0a+JiEUz5mFMmUX5WzsiqMK8fFahTtExat9h/8/cQ46bGr68Vqd17R6tvw3GC2mO2wrZDBNOGg/NYYCdGv+oNJ6daLF8uPRRzsj9KverdG3VBHub1ytfw3OrYUO9+SpLqSPFrUzkihubaQuSHj2WxAz/B1hCrjau/6gYYRfy9TQKhVm4BY3MhU4YC5eL1phSbAqQjIPNxe7sTV5faknyxG3w2mEjD1fWbh2mkBpKRAoAoIEEgOIvgtNd1CoVobgISWoYupC00/tPVLA1fP3yMuKWEqfoBL6e1L5joTFuDEpS1QDNnmgE35cJvqSmTdhZeF4Bt5M2USlUwbGJXc/p16YJCfcKiOOqIMfbNRqJ0saw3cdBM5YVC1xpF0COZqmOh16uVLfTNZkxucLlsRSWidzpZPeWNL9tO3DHjEmJ3dMvlhjyFcHDSmfnyi8bbbdejcx5pR2O5ff35xLVTupZ57xuwP/2FF6gYGQ/oDy82R3t9RuLeUYqTwGt22Nu/37NvlzY5cFe+Kk6cHKVyGyBKwZiiwb2YcoEwL/SEcNiQ+Kxym4cuiQPt7y0faXblgNi+9KXM8nFT9PDMs+VywWI5o9lZRkj3TlzrKwesI7ZfB76M8NgGXoWU2UdRnfabNbV8h/vGJYyjm+mnag/0bIWpr15zDzE/d3Sf6t/c5kRNgm2f9KJJxTl86YNAEce1OVcSdxym0eX/D42BMVOl7JF4UIc4WCF/jPV1sPGHgXOvGVEPn43nN/Jj1KndkQ0K8a60KVNoWTpffpglHr+tRlgy/x0NRIBPsEWUM8KDs1dj/zrXfdjqEoUXA7BJds/Vax/s9ILrMjxbwMsKpZTR6TeDg7vXOBeC7c0eDjq4N+5sDdiIISgWxPXz9CN9O2/sEdaHJCg1AGcrhxiec2j3P0Tk9NrfG8Am5PVEb8l57bqk33t9yjKMP5lcbEf3T0F6k9AfJPqD5lDUpEfhP6ojVk/o6aNIKi1ctRg6PFaMWT8Vek3AxY5K6I/c5sU/OCINum/LqNeh7ZmkAQCB98yjlRcW9GHk1tpmHxOEwYYtRMAxfyKXbwkVuquK+flLU+EE8kiTs57flrYvkrx9lxsB0AEcKlVeoMFN3YWGETxTG+LroHa1odrFYo5bd/J6VrWFw59y3HqTu9khG9ipusNumwLt9ZXrqRifKNwrcVY5wiRVSJRZUHxK6+9NTKOvjuk5JQz34fMQOhzyfrhCqarGaDmuKX3R/FvNPLq0fWOweFvFZRK0TiBV+T1vFyY5I4NBDiSGAVIPq83O0Ut2bLMJpSkP3rRT6qx66+eMGvlMtg59Py0YY2ARsJBzZVSs58j2AY1DN5rY2xo+Kv74YRZeAzv6UX9SspIPb6Nv1P/lIl4R6+f0c9FVHLv1LoWQH7wPZC2gWNbR9BMohXeMbL2vS/JspG4u2na1gaILbtEj4vQyN9BzFE1gUJXmE4lqKMgLycj3WbDWFIjEsdRuwNUnFtJJcABqQhOHQJP7AQy9FftZeOGFL8zXdEIPhJgZwWAhF/SneZ+9ONiNajC9pMM2SNEFePiDzioIWZBttUGndqgqQc6pTcgQKBV8jiIxkYQDNZZLJAFEJj/YCyR8GIdDtr2I24mvxqQ+W0G8Xeaheh4+3ooWK2Gk9JvhAmpJuzIqHAZSMoprLTZf5MJAQZlhPQPbdcoPYfZ5i4kuosJoXaLP8KouP5KfWqmP8Prycx0xCkXKpWMEMrbu0rexmb+yeDd+8bNGSp2vwZ28ZTM2dB40QQlSj3nY+EGL58pYXTN00C+Mex9miAn9RAa+3DXWZWum4c1GdAX01Nr8mLnMJS9BYaegOwVMgrdlLL7szMxiq2cKDN1p/GWt0iiG6/GnYvTidbEXqYfOBfifNjQJeOLzdacuXSTWqwGtsQU/pvjNbxjRu9+d7brXaqRi0+qF9eXDdvPfQ806gt6tODx5bvs/iWcetQ0c8RcqNw+tO7032rzQT57N+F7DSL1rR23i7GWW0XV5WZ1R++dj9LUfWjIL/C4K6l/T3ZvufETyTvv19MXoEaF9lz5VlNY3lX9oHyXRAJkiQ2iMntNmKJyueBGI38P3OtVHZc+YO+C955H5DzhJZy04v9hOvUP09q81xZGVVnbVgaNogl7uu7m98s1X3/QPDJ4pDcBNxI0zcFwXNUFQjwtmsC3uL6waSXTZRA6bPur694uKjnTsuhlPm5eyb7aEdqikNx89Cdkhx65HreicTxicL2Y2t66hwPDjUD8/ZvQuuN0ncIZALelxu/AgxAbadv9Y7iTlZqBP04D+YbhO4pUMqGYMI3OxOB8PZ2JHRHPwXm17sLBzvRD3jLjQymIXgZcI5YKnikGMG1uVBemBLbWMh4DUYLKOsYyLr6gxlEfAJpSjgdg6E96wZOILLl/OPIHUSpMBUCiVCOUZTIBdIwc8b1tIbfVJ7k+EO32gvJGdOaFs4vTMovK2nNAtr/LBFA3TudT02IVIsCddxQlWQU+vy6DfLJ1qoXFmmQV4UQYiNDo6cmTCS+qakbgzzO6RCC73DIIw8j8Md8FDfhTQ5rUw8zE0hRy0sRHt9JDyU8ZdC7JUEM4cIqblilCJ2PyxsoaZKErMhKjVJQMrTgfScj+d0Y2ckpFFWU+wkU+c/CgyrnxboN13XIe5Ds46CJlO6/kACFyw6evDeL3GOjd9ojxOzXC9kq21K+cfe3ItbzIaZGc4IFjzQelq+LGMKSD7pCsccdaJwk0oAB33MpmMUk0qEM30lD9rCV21w8xbzLN9C0jl03fl/35FdKN4qsT2HCKvH3eF0U1DFQJK5QQIGC4E4GDgbey4KKVCO+1tpPEpXjeDFFUbNRuAnfyl40Aie5LtyyBhgVdg14pt5LI22PktAV4ygsz6Uj3WA2+iMkfp7XIztDSIx/o5pmQEeUPJS9bcFQ45qxrjikb3H3Y+Lp1Pfm20JkwTyiNAKs75R79isbrPPz1Lqol+j+XLXd4njLuHVX7pd8/IyLq+lpZE2EuiX7n+3gYJPZyOHQvPLy6ObxD4dJNdyL8YCrAHPl+zl3yU9Fjl3RX5ehl2dVdLXYFKEYuyk2d/kXn8f0RfAS2opuAlOURy7bPcM5hENUlbg6S7fMQWKsbvFUB5DF9NJ+j1KI3Yp3htxxnb/qgXDemjpx0tyFGbvvm2f3KFALY5w5/fmu0J0t41xzvodn3Y9Ah8KfCCeDMpY9HOJ9ivDd/g5kubWhWMWQouJG5JmSZTt4rb1SX0LGRyLM4oNOI7uvBxCnIaTZWqL6rXbaply5yy7rP963DMPdPW5kLby2u1ub9Z4ujow1yplSkaQgnoKl0opuFRNFcqZNdgw/L0wM8s8oRqbapLRFtBjHGGl0rxz6GhqhiaOClT4/Av119JHscUfZpBKu3IhzkF6GHiN8NKeRVDupqqBLcCRpSKreWZ/HvuLGAFjUPF4pLjGhxN/OTFygkZEsxTmBT4NGj0WVwpsRvaVVx2ULNJ2WBccPYi/LoUBVJPCfAVzsVVwvSCBdx2DJh1TcwOiF1pBhmbUjS7hXfs76ZwQ7gERsDArcjRJvHJNCzIDYbgAdFI8OZsztBDbWzClbfswIsfWH7Hex+YSFHekBoR17zmGoQixhxVUpw2sFkzomX6sTQCvWGeYGzEW91IgQCghaf7uuYjJ1Fvef3phVcPtsstEj0BQxW5NUG0Ut58J6iv69gWdMw6Mp7+FKcceFJCIWBSnJviqckQaQZdVFvFbfadFgDyt5Ken47VOTy1FJIXatnT2dP4EW93IoKmN7oXtbOkP9FoPpwIntcmLzYwly9oedNYjzH30y22FCGp6TabW2jlbfvoA8iz47bn2Vub3v6UjL8ONfX3VSZXdhaipZF6XvM/9YNptKuGLGBpv/4YPUToCrwMjv7buvZb5L8jA0QvjfGqBxqJRKLoE1xNbw3wcesiKOZEXgL27ptrp8ayBlTujyD+VFNQt0c5mvT0AlhOt+kZCc078FKpw+Wg5/O3+ASNRo4tfonc83/KDbi9iUVEsknlbIXoQhFxNmysakC8p4s1KhP1i/NSLWK8psKbs7OGSNFOEWIZ1p2BGXtHjb+ve9Wvd6bQ8KdBCWwN30yaoE4mK6eZzpfv8rm7HR/K/Qhfq2ijbGLUuZ0Lg02+QafcWAOB4wT16eWHEyOs8Efd9YEEupm2K2VJhK+UN8VXtTUeOxCthQKoqsceEJpz9RWaJU2vQKhees2y3euN1Gowi9B6FXsRP9pD+nYpDLeIj142/E6lxh3fa63KD5+Zm6sU6dPy+sNS5UdcCxnCTIdgXfPcI4S+mnu2BW2bNZknFx/1B2lT7F4Gpz5GdmWa3fNAxXtSKlTwOTGSTK9D+zzjctvftA5TPzUE+3/nPVwm2VKGrEMBMvu2gL+eqsareCHwwtLUX9kPyCr1LePygdHbIcPejvUK4vX8RyYp+Z83VyzNbjw0crHrDIrAHjuUvJYS/0CALzdncoEHmFGBYgKprmhJzifLeFp0qLi9wk+8qXVndxdPZXuy+p9eGqpGpeHNaPtFELaSrdPvBfNuWK5CdU6dbMUTVtGgc9BsdEb9t48x6ptazB8nwFf7bz4JciYS9iMVllEFC4vUaIyysBV8gadCuR2/Oz8n/7hff3GBoHyJ+4x++v2NN8LZYkG7/tXfbTQFIzh5dTKtp7fRXGAjjA0Miez/w6NwAdZDTuzIb4dAF/nMRP6ha5/RahXCLoOOBDdqooRG9IDP57oOVk4k1KtpUIFETKO416oxbQk6/nu7U3Rr63cnQCbEFdt4n0QJFm7J+pEOzepEI0YqRnzRx6o8JJnT40IWoisUJKG09elZ49g4ktlzOXP4fta3XJhkPpO4+6ScQZmDUHtIeUdbz2SZd6EOfjEVy86enHxeRRqF7oBmEtkl+iECzaoTTdBfdGIX/+NUN6h0jSjVCguvqGIlhU0JqWvhJMAqB4vQuW0MBp/dQooPK91lELD9Ot2UQPTL0wjvJgKOTHt2nLc/k0MXrZgU/5jxVs3vjKkN7xBsyLm34qJM63zWquUPH+pdgl1aH9e24uXE0uel9DB4PzL6OqUqJBMpkgE7I5na1UKt7prowQP8dK3AB++W5pkk/aVsCGKNnFFnPdqoykDPwy/3OsSLGg54Ayg0kHr69NLzfnu6+LTWu1vxZFuTTmLLGxSie5bJPfeoAs4pNhYGxljSETn30rfhVS+oP5WCFCjjCcwxHEbEr4IZedHW46WyOzmGsDwxGWjwSOKkysBnTqkGjcu+EQ2zduPz0eX1UCiwk70Q92mWI+9uIKlY3zf00MJlj1OfbyGAQh7VXWCtOtvfez47+xIOda+vc47MYz7/CzWG//aB6vKbLAd8/YG1J+Xz+bfPinqPKMnKrt0QRwZss+b533H4MKLz/CbzLu1MHGqVM4dS4S+abCny8Lpu0+CN9cM1AGJW89xBS/dtpsfDfthRva4fvwKgCWyi55Ps4rf2iMYo9KedhH8DBONs7DvCx2aLYAv4NWj0p4NKNjFITDIdVeHVJOALNV8tvDN7pWLLLyFqwtaGlvEZ+UQSjVD8TeCdOY9tRqZXNSzowsccwf5KBC5YpDYhRy6T3x4et8gH3HpLiai0tlPR9K91DXNPN1B+fQrRRFjA43lyHvSoivUa4Zew3UX8dYmO4wln18WxseQBU1gPktruNi65Bz9FtdTO9CohA/NayT9ByGS+0JsddTPYrlYestzSReSdFAEJspJH/m6glHVMhcNlHP6x0XqmVEemOi5FzyFlaYcP4L6XkKNZgWgS9uFu4EJjTqVhzP2n2HeS8NZeu3mT2m+Dbx6w+h6qwnasmokAmb+E61ouUyYQILbXf5z6YVJ7/iGdTyY8xIvpvsy7gaxbjjEkq8RMejISSvEWh1hRKAv+KApF4fSC3XV8ysRGL+jsVzqQGYeYVE0dtQcjar5NH0CgUxxYQ9Q8dXX34joT067lm2NUSJAMYrJGYdHBjiyvo+6ctZ2YrEDlftDwWMfg9lGWSMFHurDzlkGJqoyuD1HyVkUV+EcQdppKgvkBNQ0b0QQadHTv5kUQGd4taXFi3ou2PELCZJMHni3UkvuYNiOHs1VZnaZOZjK2XQMuepEC5tuDPSFbCORIAPSv/T+yFGAGeul4ROfFD8cyxazu6OuOZpujjQfprx6DDcCmTwWVFY3D8nMiF7jSvcXkj4p++A5cSrWx86Kvjznr2Yyvfze7DJuCOAZHP7kf2uTYuysLyvZ7R5ueYTVqG8Njq/edD848enZXfbIOW2J69M0kOShmtbqeuSvG32Xu2MVtrOkdeI4fp7XqemWyZe67wXFvdqYns8LpX0tIPn6/5Unxvrz3qbfBf9Gt4eF86JizsfIdKeBiKMsfMQro8wfNlkufXsIOMg5m59lMyTT+YNH/xq51ScxdJGL+5QLn769gyv1cZW26icymTyhMHdx7BO33rIo8GM1Uz8bYMlu9CyfrGAsR9/1tBxzqSN292iVLBImqjPl1e+vVW+bnlCs+rrbAbwr0AXm6p8yGEzh87q2qQX+wPX3J/vsfWRVcdgrOafD70aDtyZ3TJNZ60UTWOJ3OZOf2RGf7GJ3gCDoy5ic5RLLlxTB8ONIcMtpgrBYSrOFAa3LQTe8k7e0hryZkzukYrGR9X00QWcivQykbf/95fq/tT17V6l+iFtjn6COF77snwkJI4zRV8f5iGT1kQ1kk9yn9EfWUWmhHrbnP1umMnYgq/ljifPg4vKGohp3qiGOYQk5FRAOiU3YEVMoByWJrR0v+zZXcLKv9NOmzCMZKGYtXQSENiNPkJPuZTpCeOwhABopTGncXPjW7Z4TrNWOIlaCmbM05/Xp8Ey6DBYSKkQo3eoMSk/NhVtVBGaNi0EKXVLg6M/0rYF9lbxYvDqyltGjaVuLBo9nLDAYeZy7TQJGzBPYZf0SjoEYRSCc8HeZuwlNX+niTHULmDmixv3jtApjNLIIWljGxLSSF6bXltNRhkI0jkZsBI3LhLMovRoJViVJggNA9TaCoFlTH4eDdpKUUmkjzVFvFqDY5Vh4YzrGfZEs+8vVeteO0aSEKfOfnik1qB2atgqBUyDuZQDIS0whvPR28BO0JDhF19TWpp9/CeKxEAKzMq7JyYhJqBXP1Jrf/wWlCARKgpU1EC9KkoHxff2OOgdFgu37l645FC79fkE1F7X93gsgnhm8uy84mc/E1Kxev6ZvUKGdr4o29Tnnguie5guTmfi21A2pYy2UWHgMHqbRKFoXajwoL1QLdzMscsoepixZybcD4Zvcbu2WwD79+io67cKEucHDfnqER+hyaglemahpQvaYwC+iLGKeYhM3vA/dxXmBwjR8AwyJxZ8foVUQ6pIuTeUpI395WNW03E7i4h7p954oihh5VD30ermPLLevgfhX+bMyID/MtIgaDvYo+LdpwaBD3gTgxZx+2f2QZDEpAJC5pzMOoQ/g1a7F3adsRr/jhfOU6r/+DXPA6VbUUYajG8VVdbqlab6aFV4mCC7O1fuGc6vkHqklxs+hgIVxdO6jl/tBLJmO+qf7QOgCPYboFpGNxlhLyTIFhfiM1PEXaCosis+WvpQkRf30banrY9a9doKqZx5Z/u2ZI+dDaO9K/OgNq8NrIpJWS3vkd2jJstUBm9WDZofTF5Qr6l3sYp/mRVpjirt6cakTiRAHbSKoBLvWt6azfVQ97IRQY7+gj/Pfcput4nvNd0ASRbg1pAgCJTnqAj1HjbqhMWTGHJM95IkDF98oK+dbfymtmvBn6mxdtESFlmaRqXrQuaEQqdKyEvaX9dPaGq2c8RzLh++8izxoIVGz3FV3XI/WEj9G22tTsdPR+k1Q72gHNNaYh0TSLvCNOzb7U7p+eRLTJwAz/l4WyrU7OSi5GOYuE3beq7nwwAHb+RWpL4OXia0p/yE0xzT6qXFc276nB4wgVLnbEfI/daUSgjt/Y4y5gk4M5Uq3j3L8FKkPu3hUDEiTfdidUOeIq7gC2BCXeoswXzqRVS3mYOqJ3vR3b8MGuP9cV5XNG8XtXoxmTDqzyHX0DKPUKcq4KkkuyDtZILk/PzYYalE552k55tu3dIp6IEhuR13XBftFpn/MLK9S4xsUrDP3xEzywbfNiPEDJKqhu92sSfCkwgLewA7GdtvUi1eCq0pFOxQXQ4JmltSdwz6mlowWlX3TysVvA0MpVaSKHCueG+b6D3UbWutUyJTgdKrz8rW4Z1QUCR7oviZudoYpZn4pvb6uWn6ajKppgM+8gjFIE//23yVeecSUZrK3CvkY6hA4d4f08saTYfzuxwOeSwyGwQLwT+6lTgFFs7uAfPcABNaC0S0JwqRhvzPzNSy55rZMsabHnDc20Mu+HcBAlm0wh7IvZkULeK4PeApQ14wMZczquzqjalOKfksc0+oEVeL5SFo5XiQFUoUmEJjnGgbOS/iMefHG+nm/W1SydDAR1lHFLAS08wlHMMoTVbg7R6Y0aIA4kU8K9uGSVjuN/DsniOW4Ftsf9n8JARXzlNYgaXEfsWxZ0RSG0ja3R12fv2x592Kk1mstkymqJbCkQHPUXGZ97sRKsXwjEKXDOdgRor2prdvBRgP38glY7R/pA4iokJGmx9AVc7zVHqklj5vIEqFgSF4f/DKKKC40U8quYWippSjNHkLectYcO8DKBbz41eeKrsNDnQ+Hr8api4mUVCCoDU0tWDs86jPlqxMea8FKd306fX2GSLfSs/DBiuPjHX4EnbZ2qVfS3o0skZCBrS3roOrxFNbeVN+YivpmnlW/wt1rOFJj50J2va9ASarX6P5HxpHMmfPI9sKcQ3b+bndkv8KXVzT36bexxbJGV6/4ORM1cZTl69s9DiIcFgr9rBVzBzcdCsqwlqD/sQcccqd+bDjHnH69VNTmzXmVS2FBXBeHSlTxntSAeabf1B0NHw0C4Y8RxWpGYIPF0BjjqOS3bvUBgvIPp4zDCo+IJqrt6diljCa1LYAb98zDe43FdoOuAHoX873rqXItQrsRbQkj4wQ30/z9mmGLufhip4Q50NI3pGGf3AlyWCr7GhUoEh2o1BJMg9LEjuGlpohKUlJMY08HNgKKxfe2/YQz4pEUo1wVdT1nlSsmZ5XSuly99qta0Yy8xjb1Rxxts/wKkrm9UdKzyJ0AoxoOyOfetm7Ba/Qi8+CpWzJVYVFVX5B9Iiartxk6DIpNSKeX7oruMZoCFTMNF2b7f+yM4tFE84dU9o4UZZcCLbe9lK0N6gIqvh3qaAp1nG4beOIZtzsnjJncOR6IXMpcQtDKWTEfkSiiDgDjKfzJnlg8h9lnTinffRMRoM2a13rNu4IdZs43ifkInUy53OvK3ulhlArZyZfDvoHRwm7Y3n7vajgLsBStDO1+Y7yr389FLrfjBLpsElIXjUOTmQF3rK3Xn/8TzI0iVDORuEnZUnt6h7d1nUPXFgi5CahHhSo2E42rOP1PS9YyjXPkVbwn6yiastZrfp2yZZy/5pmHI18974DkbJPLkEATxNprNWgP+Fi4oPId/oCIY9SScmXCIwMG6hNN3Ecgd39magEgvGVRcXVI2P8+Gdkz+qDBHSkHdw7bhP+ahxff7BZvFafKOnhbQTwcrStlajb0aj9Nb0DhM5irtz1cR2gxNMTpkoNH6c+KOfuqmK3u3k8TSp5T6EjiWr8srwNYhNUBdTbEz31bXlV/RrH26VK/Iz2RYuXV0SJXu+cQx15r3ydW+XDWMZl5STQShLp4VVIhfLkBw2RFMmCzD6A0p5wA/xrsEDt3yK197CXN8D5cZTlUeycb6+8PqdfH9Aw6i1WWp7KtILOmCnO/8Txg/9lFkewbcEel11EJhdxenP32HSGd8RLBWFhJ3lQ8qIP6FLOBNR/K63ty1Ov//lfr+nY3/Fyfi9fcVMpcI8kOqIJsknqFjqN8hlDLhdRoo9KiYqduquFso/nIMolWk7xMnMEPKaF00yXE5K5fjHd9u+hLRPS4wrqGMkekOITSLkOHRRzlIEEDOyHm+pTmAcJQE+G4N+4yPvTfwekX77XAhllQcOmFdMLVtW09hc5BsDMc500o7gqEokYh/SXHf/k1rgc5+rY8Kv1Xog94sv+Q0KmYqTyWLWcBDO2vQ+2iNF7ICSB9qCOiRxezwtXywdsj9ph16VYGs+SKGwqfq5gVZ81U3u2wPPzl+LR13U4ba6eOt+z4zI6unbYfkQcPzbz5aEEU9MwuLy0qrODy/LdJib6pEtvNjAFnIqXIOOI4dZ+51TEgMP0FqpJBFKu1IjdAl9LfS1G79IGQf+7/qzlBGUdF1V002227QYvl2XpHJz0FZINCL7RFRLsMWpdgBP7CNPX0ZaVkkbku12kMiaVGPrzig8vJ6+r7kCUHGzxOZDzPFF52EEbjONrHkYHyn4cJyC9yL5Mi0tU6THV0RD/hVtuXNcH/g44cwR7Tp1hxpSOady9IqYHRRcQ3Om02wRTbUUfuBrlAcHEnt4AHslOaiCuBbX3K1bKHR43xrlCCkqkuKaHveA+iHX24+8F1rbrHx4+61NeMItkLwbtaeODYUYhx5dJtsZUyZeYPQPjYcNOliTUJs26YTtPCuLysRnuBZ9x9JEk3VzY3papsNCXO2UNmkdt5XcUp1J3upVfGjJ3hC1vg3puAOuGRIl0dpgrgjWoXSiig6Pa2gzd73BxiafhUHVvIqYnVdnDCxmK9CoHvard9Pk3sdM3YtGfb/Fzyv0RcuZghe5iNLMF6WvKypaAfIIgOnm/xIqnV+M3BNl+3VylqyajdUDC1Wnz493eefKWCbGIBE83ktPXOCaZgskMH2RFdkXD+EMwSHABHweEF+Y58oMSvADoDmFswupO6TI+4OBys3WGGM18Lzq/GH1UQp0c5ej5E5MSkQlo2Yn57IhihlR6/posQpjPDP/dmHmK4WIO8yRCOCTBN4CKNCx9Ma7fylAD9DBCAf+IzlU4RXxsPOLkt/ODtp5+TWnbpnauZEXx9mu/BGEvcae9E5r2QnKseVhuH3g3RZ2e2IU5BvFbB5yIW8FpWWVzSPQmfjvHXdf/zqn0MmLSROX0rKLoiXp2s8DlMysRcjiZ0a8Pp/YyEdd+04Ya8nVy6H+eQU87S53PyT4kbG4pJ+H+AYnAAKp5YeEG4NHRc6bAq3T7DqqsI/xZX0bMqCWvXzOuH335m3qNi1e5jJSifEpiUqJlvhVFTbNcsGHgRtZuzswDEBVHiBt5ZeZ4gUALjKY3wA/GP3xGsQ49nt+G1xOBjP7OXUQvDE4SYf0kbzdXHHYOTjXuphD0eVO8TkmbntyWqjb0SVgKG6cKIC/JCiFZLhdVbduslxgDvolbQjsKrmUcmeprgt73XZFbW+c3gI6pBPfubPQ88383wENAKOtnL6RxQPLySAudUus0Q6MqmbwCTxwW+Gk5PyeGKKHUfTn6zGthKRI599YaOeSD2dBOASB51HP7jztrd6iHvep997RTggZh+erC1EtYfMi11Dbdj1R9qq3zA5RXRKnblAXbcaHXrtst6vWj4j6wAt32o3e2Ep0+kB9SL1AraKWmEoXTtqKykGL9joOSb65RZKfFvejZA0bBs3gIT6v06/sNisGb4vill1jculR75p+e8pI2Z4AuuUb4frxHQATHqwrGNB/IqnHkgj17flXBZL7E1HKBl9D3F/yUViHwk+WCoeIHxGxtK36I4ePKxeSfXjQj4y1fU9NQim291SaSqR7BT4N4OZ5cfxb6QsaK5T3oFmL07OvgiRRPCb7251zxopcEvL3B6JPBR7hc4dIfAhJV6PLsxkuKkqNcMVnJ6OnaggEzLauEW5wZ6NKI7lgUYMXpQ2P03cv6vYx+pmBgJe6EpMOEoZEL7QjBXDMzxmf1F3Pfa0KZXduaRTn17GYUeCwkOrLwCqzQA2E/oIU6bbDS7UCNLmkcrvBtXn7zzNdMaCbPAFLxz79PrxoVPUiiS7Tgmv5yvj+Pg3Ie7q358J8UqWnupURa5QQIwCKWWyeLvFU44ZQROHGObHcgezAh22FOa/sO9MqtLuovmhUBSxqghhs38rNNvx/eQ3ZRQqBcmJ/KVy45tzLj6YuL2Ee5en67xWqKEL1Cj+c4cfSO93NQmv/EbsyfjTHr/ttDAmbkthEVIN3/hPULSvMgimYN7jtMWRwg//5y8+6okgVw77WM+Plo3Rc12I7drKzrAbER+PKHiHGRSBim6d95p2hGCH7ZjInIFCcQg+lSQuyZesYw1/WvVdK+2D47pyW7FFcl0mYUA8rRmxHnJ6yqa6j++KlNqGPqSGq7H/iiuuWYu8jMe04G2FtZ5jkqJA/9kCzvcN/3B9QObh7oJJUUGb7ZegPYFbnMKP+wv0gr4qgWE9LNpNo1kA0vNCJ+Q+Fp1IW9/kOtlOGU1V9XA6EsOzspn+ETT5qy/xJ96Wac6U33R3Abqdw7AqBSaHUkTwQoDFdVe1W4SmI0HVbFSr4i52TSf2D0OMZN3qTRPUs0xW8Jvf2tD/jOYm8ARMmmnKmP7xC88yLcfGnqjxfnTh+j04h38CAXp+ktfG/vVl7A2LjZ0xasIUTK0oIJf6dgVUuMBjAyFMiDoFQg+Rmjt54TMKld8PbfkHUt7+AuqClOcNDk/rsZzIjpGRQxKJlK2L20kFp1mFreSn2Q4BHIM5ZnF7J+PCgrEiIote/z1HWmmr7HXvn9U4xuuz3NcqoW5rfvZmlU8HoAJKRYhbtmciFF8axCooMq6XNjyHjoMlCD6RVgXBXVItEm9h2K0JlUcvERIYEQIg23DO3uRP4MYRi0UInScjj2ElL7bAR0RnyOPmMXNnPqi1QszeDQ4LwBlA8q1BTQzD83ssBnEy5oqAkDPtzZsexQweRDt1i7k0lES1TZ/qAJV3pF8C1QS4TfRs+izjCPvcIjyIX+2BETQ11qQd1ZfosZ6dUj1ZZG4lQaVShdckeqXpb2e7d+MRN5L06OyWLzUPr+Z/nPxPmr0tolZMXYztHHZQlQgiv7nEsOTfcvEA+bb8vZiJlcGozpv7ATaMrKIvXeKfLar108NO1Ce9sCckT8r/htDnqVYaTebvG8Fnx8yGPxquvPbuYl/1LkEdf0hdeEUWZbMUqdBuVonwhbI6K9FH/xxtafZU/SvWfKf7UkrGVLyuH0kYgh8uuivCRr9V5MNptkdMEQlkGyQRYqhrpe0+fMRvC9Pp0rISv/4upD3A/aGho7Z2Geke58FdkNlgCfjxBHaWDqHV7AIs+UMzXMEkgVBtZxNlkceCoZmaTsSF6eKZd8tSZiDbN7XuSQA9JIdrMGH2j+DdBxuXFfT8LoIw79nqZaw/lXEYZH+Vcy9Nrsq4kMiTH0FFRbMBrJd8h27cz57nc/xXVuCbDT4Yn+GUuqLIS1dapteIla9jNZ50hlciibbzxNo5bTKh6Rv/VNcMr2z8WVMjWV1D/L9LEZsfn9Nkd/7keBLUY9VDurFn8mUzw3Zx8+uPfaEWupHMB4bIT8TSKQw/Suk10OD/kND1yB4WiMfAe5Dqd9vqojtwdaSwDfruQyxlwpwjr2jAW4Afg/PWXv6nFMhyrSLOpQQzhHF2SFtM5HiDwVz0ooNd8uozhDjDDj7ELPutq2IsMzmoZ5lJOkCH8YSYGTtjIH2wBv+Wgd6LkJe3SeQUikUv0oXzIve7hDgQ5ouHVDv295fKznCxmTG/1Us+LRmdEtb4jtDfC0WkC+aXhdY03BT2CmgktGp7oA/VsdnD6L3NHro5rw3RXX0RV2zozKXyat5mYW1iJjhvL8SLTdL9HlKPKBV3DOgDA7Kery3py0mG1kNd0LPm2+X+EO2AkrTWU794ezkUbJyX8MInLLQSikKOlTXxPEzDPgoSHn8vmD+L50Hrr07K0xZ6FvrKuSrCH4pLxny/Z9y+/pCn4wunqf4ReUE9/E9mFVCBV6J72IG4DCfK7tfUt+EF1dXg22WXxIZZdF5J+DC5hWE0tToNnz4M5J6NAoroo1eXoD4AX7G1Tf2ZMi7SPUBjXTekj66eaola3NrP7LytHS1O9VLrAmcUSZgjQYeMq7FBvtqX4vBPC6VEGxvikoNh2ZCNV66JwP71xz7zzFv/6SMgMo3tN/dgP4LXOUcM9x+lQI1woAWhqQZePgWAXPYQEOXo/Ia7DUnqw3XNgDUga7vk9BbCUiEa7K2kya8xYq/2no6W7vdcbX3oQjefRVebJyltuBlphCo+/cwkq4RiTskIeu1e2UHpSHhuvtSAjdAGOyg5S8LividquY5G/lxYJayyEHuAWO/UJikRpEaOOFuwoHHp7axa0VEYxk3jiNO2Ryc3ROrtJqVbnS11zR5KaLsmiyJ+NYVG/z5YlpO7oDY9c8rNweFXZ+/exip/2yh0m0NxuglnPW5jkelP5up6QlPCyiXegI1wttK99F9V7+ZrgP285SDc+1dtdkZnXMU85+nZ5oPmcGofhVYiZ2bsSLHEfwP7p1z3Zny4izwUL4wzg+Vz5CNGO/I5LbfB0QYioZaImUFAO8m7fOjcS7Pg2QaHiH0G5G6OWZB+BW7/PgQg8lOHopzXQvbaJdYVlq6WcUjxC8cIed09ZcRrJuZhdOX3wTY1x0D3c6ydO1GGQveF96depEVL6wD5Jney6mrOOGPL8wIt3VRp6bvNtVDgixZ/HmPQGSMXozISfFnK6lVPK2otq/ooDhEtXVH6xiYRvtBV4B60oZZ5Y12nt5NHaQLX1K+QoO6yDjvyFjqqC+Nq8wKgSBMtN2PNzq58up80RvxHKUYpIJL8Z2MTv51SsOnhQ16sLTQrwctbwxtkdd2bpYl4+XCcaQOpuqJYNXcsBHjsJ5T57051PvdsW1QqvpuWrDWqhzoVKrPArp/6zHHWShzM+2LPjYGmsFvS0CNV8DuqR6hJva1V20orkQgR9UaRRv+3NsJ7WZfCxVevQwYkE+6wVLB6HqPvQgtf0689Fgmqh45kyYKoyjNy/ISi6WKr/LJ+KlWIwLt1Zf22I65LC0ZnDxRRRySCwi05i3uZshHNGOgF49uqgMdAL9kpk+G5XyfNfwH5uGTMEa3OQBEKUh55NzrZGTsyigGmvL/iKy7wqjzSVC7eQlT9d75SYGEGthQ3D7ypLX0rKZCs+b1RA8PMQRchZ0pAuD/XDIhE5BtfIa2GuuJoShKdyyTOnv0Kl2CvVuYscRadHj+FPI/G25sJ2yszGo+AOFzkh8J7ZgNdFom0z+odHR1WJB28gYTzmfxuINoHjnfFSTnzHFbFdRUwd4rFU+WGtRiphpHeYYIvw3YPzxQW8P9afwwmhDUUvaWZvZgSFlOccm11m6vl2EFMBo3NfG6W2ceAOIwtFHmY1Uo+DpcckIMbft9NeEFfCQNd3YJhWn/hQVa7NdDGvgRhML8LDXaVgkhLHdNtxf6LXvanEHW7gR5m+0URrap0Qv+AbIx30rGBmPZ0qJptRsUPNRZgE0WclmKgdxhzKNW9pr6k3OvJSaSrbNyvGDyAe2jFZq5dcMPir/FUoxcAuSBraveyR9YiH6ymhUwOsESDZYBnPg3aIsNWSggfgmPsNV7Xewj5/UoG3qUt0B3WN8X5XkUqAmRL4ySgfeoIWaoPKB77VnFLotH9+Zaq8JM139TqGbQAv5no2xOPf9EtW6PqyJ0BsDDX2/vRgQpiW14LLB/MB4o2DTrUpKR4bUW84hNVv5JcmyqGW371iM6WUXYL9PDTEsEUUsM+bwpCnTuoXbrTOtsae0xHdHiOvukg1yMv/WPjc+gRZLqOyNnDJqr3KBnOdoKlP1VkNM3g74aK6qoqZyiFeuMwr9O3z3dPrpmrzgZIoaERSvKGTtV5MXdZvT3/1TITzSUek1Iak+lbCWE5eg0g5cqQt7uJwl2MktFf3cfANpoELQ0vTbHDBpk9e2E8S6eyBXb0xTv4WNbA3JRetTtvlD8IoVIGdOhactB13W92UMqH8gF5Z/R2QKUvp2Y/pIQq6lWeTSh3OScL5p4gbtZvbtUPZnUWSXj+/jZnl/I42+lFjnf2f7FIf5bcYSr0WNYWViw/5MHsqvDCKzgvrG8EUcjIo/iHeKT80nPEUzLrCmtDWBX/52w3lTr6d7+VC3aS6b8EvGOLezPdAvU5pwojKPNTDOhUYE8oZzl0xdaM8FXLy61njtxhS358z6HruGFjgosXwZyXn7+NE0K4fdMbelUBwvdCnFVfnjpjLleHlKrIBHpeHD7+8gB6UZ6osHJ5y0Eflw8/Y2TWO8lnas5vr/Cm0FkvpMCQxrIpEZkII5UtuH681Xa3t95zEMj+7GQf0FTtJ5oy7ByPV+f0NV/MBlAikBHcM3I/76H9aGJC4ifCLHyOecj+oqXaw2jymI9UGSPwyc0jSdmMwH+5uH86hZ7eZirmBu+XhZT/X+dMCYffKo0yYPGIxj/GjbyWzI3cmLGc/jTRGivuXHT5dvP6EUZBdfMByD/dINFhAv7tiwE5JHR4wD+lSfMwByGJ6biD/PkUnKjETHPQjzACPwalJk2EOh/GME/wDjvWgBpWNSWP7lx32nB/L/AApAI588RO+enynP6A07erEKshU9+386bKjNgyIko7HaQfzANAxytEuEVnQnqi5HP1oxtfhWx6Dn+ZppMCgGSJ4yfYmpUEecxOxP+zg/oaAuIzqVJKjKjoQoP+fxqHfDMN6QtGR3CBsfjUzSxgfMqs49gp/LgVEsYd8pCQOxO8fqpI/SgB2Q3yERMR6qymmqOTgMMHqjH+oxQUZeAGZT6yN/WmojBgVWNSB3UH9RQA8iViCrMwHUMBmo5HdXA2SqT6EZ/DNPZZZTjMbcZAwR+tAWSPKyK4HqGyKLgMa5iAIdWBxyHjcZ/wC+aljIbJTymHoboqR+BGaj2qSSJYAfQyc/limlP4hLz0IS4xj8CKQzGCEg9KdyPl3Z9qbkdqUggcDNeaeiKAB/Dg0ox/k00cD5TS4PQ/zp2C4ucH39xTuemPxFN5AHGR3p4YnjGKLBcTcDxn86CDnOAaHK5w3X3pAQM4wfpTWori5254P509D3ww/WmZGM8gnrSBsHgk0xMkPBPOBQBgcmkDbj9/8ABh1prjBwV6ehqkSPDgDGeCfSnJt/hdsj+6c01WAHLOB+dPVAxyOnr0q0S2Lkqc7+/pipTgZPO76YzUZ2kEZyO2eCKesciLwkpDdCpBH4itEjNsFJMg+dB7SDI/Mc1MFZMAqSDzlctUPAXc7bT0OOP8aVCAgGXx2OBVIhkoKF/llQHuCf/rYp4WXAzGHXPVYwc/iDULSKwHzsGz/GhbOPfBpi73PmBY8DuGKn+YNVcksliFAyFB6+bEWFJs7gW0nT+Bhj9KRHlHyh7gY5xwwH5inGSQvuMu4Ed48E00IlR5PuKxjb/YYn+dLmXO0NuIP8SAEfjgfzqqs8kmUTJx7HP4daeWIUb7h4sH+NDg/+O0wH/apA5VLmNWU85HX9TTvtcm3GIpCeoEoyTSLMxiAEsMynjBfbt+mVp5UpklXUEfM67SB9cGgQxTmP5HnRuOMMVH4gU5TKMIs+9f4uhP601WjZhsmR29AQCfzpXiEjZIkx/DhSp/pQA9SJVwsgRR1ALA5+hqOSSQPlHZk6HdGGX9GyKXYzsC00gAA+WQkgY+tLLsAy4jZfTIzTF5iEq4Cb1z1wWP8AJqVkVFwWT3AwvP51EFBQlYp19dkoOB9D/Sljl2DG0qPWSP8AquaAJUULFlGmMR6YkDKP50xl2ZLfaSSMZQhf5YpubWTAK2jk8nE+0j8wKcEhYDMDRoOjLMGB/CgBqySopxc3IB9X3D8qUTM/XypeOuSh/SkLQ7yU+Vs4ysrKadJMoB3yNkc8yZH60AO84Ku1ohH7vcAj+VQsyMDlI+mcodxH5c/pRI0ZVSk6L6jzF/rTHdDhmdC398Nn9QKAJEaPH7qUK46qA3H502Vtpy7SkZ5Ih3Y/HBpVkAjCLOx7gCXd+h5pjsjt8+8Af3SQfxzmgaDMMoHlzqGz1KMn+FTCM4yoPHGRLwfzNQb5G4SaUL7YP58UqxOq5CMSfWILn6HFAXJjIdoB3En3B/lTDIrNxknHPyf4U4wkgMbO5UdmVCefwFMCtITmLzMf89EwR+YpXDY//9lQSwcIbv7oethFAACLRgAAUEsDBBQACAAIAD20UzwAAAAAAAAAAAAAAAAxAAAANWNmZjJjNmRlNmU4ZDk5MzVjYWQwNWNiNWExYWViZWRcc3ByaW5nZXItbmV1LmpwZ/t/4/8DBgEvN083BkYmBgZGIGT4f5vBmYGDjY2djZWDnZ2dk5ODi0eEl4ebm0dSSJhfRFZKXk5WSkZGQUVPXUFJR1lGRsNcU8fA0MTERF7d0tbCyEbP2MQIZAgjJycnDzePBC+vhJGijKIRyeD/AQZBDgY3BiNmRiUGJkFGZkHG/0cY5IHuZGUEAwYoYGRiZmFlY+fg5OIGKtgqwMDEyMzMxMLMysrCApStBcozsAiyCikaOrIJByayKxWKGDVOXMih7LTxoGjQxQ8qxklFTZxcYuISklKqauoamlompmbmFpZWzi6ubu4enl7BIaFh4RGRUckpqWnpGZlZxSWlZeUVlVXNLa1t7R2dXZMmT5k6bfqMmbMWLV6ydNnyFStXbdq8Zeu27Tt27jp0+MjRY8dPnDx16fKVq9eu37h56+Gjx0+ePnv+4uWrj58+f/n67fuPn79A/mJkYGaEAaz+EgT6i4mFhZmFHeQvRqZykAJBFlZFQzYhx0D2xEJhJaNGDhGniQs3HuRUNg76IJpUdJFLTMXkoepHkNfAPiPOY01k+QzuMYS/bjHwMDMCI49ZkMGe4TuLqIJIl+YXhtlT5qSklC3OLb4nO+3S76jr7xMTPq29sK1I2oKj+/h21dVRtsm+s4Mn+/b9Yt/XW2676wT3iu8ijEXTRRvLbarKu9eEvpN1Wyx8RCmT79LLNunwjQfz5jVt/+jAubWWVWRLALNI8MvVfgv4Ja987fwn+ON2yP7dW2e9d7p2+3z/yWPJs3dYHnhXzxM+7+U8u4tv6nTuVWxdm+87Z+lNJdbyd6nM8wr79v7Vvv9P+eW0WesbTDvWi5Ydz/m0WPC7pJujfMf6ft2JarvaLKWzjFdtrmKqNGH8Ut72/v0/tR/vTh/ZnzLtvNMl0dYNk6WXTm3jf/pP7uvrr8Gel9eW7FW7duqcad89iauCIQnJouVMDdKu9syXuhhaq4JXcBRemp75ZQGf8qOn32/YSWbzz5FMjnD/w9nwz22fi4xpbe7HqY4/4lenGRyprDjx8vfRZ/sKdv6ofdTtz99blat53c+ws+buq4L2hdpzvn9ZwL+mRnLF3OiDs2w/y+y5NnGz/LdtPf+27o653pDy2YZxwa4VATlJD/i/uZZUmjC80jSq1VjAHhjRucq4NGtqfnlpFcPzfdo2+Q8y38g8fP9OYUv/q0v69g0n10177bZl94cvs2w6eNdMO3an/1vZo53yoifTV/6Yfdgq9czipzuz9+vM3xPoZx/E/zB21l19nwvs+h82fT77ISWqev79l8GeifqyPjkO9tO0t67TP3zstPdH9w6dhAls8zzeR9pyr+N/tfNP9nLzDusLrLe0+m9Pv9bF8GDxlfgLl59ejZKY5STxVpZVJIDdePmRUn6R+YIxp97reCVv75mnHPefoXPdqs/x2R4219zyEzIWNVj+tbv16PVR+Q+T/q6ccJp/0gXGg4GX7b5e+7vLd+eiLob8b81VUhqLGuz/3wQAUEsHCFe7Z4pnBAAA/AQAAFBLAwQUAAgACAA9tFM8AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1X/Y7UNhD/uzyFlUoIql7Wdr7FLqgUoaJCqbSUShWq5E0mu+YSJ02cu917nj4DL8CLdWwn+3FQOMqpfyWZGc/nb8aT+aNtXZEL6HrZqIXHfOoRUHlTSLVeeIMuz1Lv0cM78zU0a1h1gpRNVwu98AKfe4Y+yId3vpn3m+aSiMqKvJZwufBKUfXgkb7tQBT9BkCf0MWwlZUU3e7l6i3kuj8wnJJnqh3Qiu4GpOV18Vz20+fMGmwrqZ/IC1lAR6omX3hxhK7j22votMxFtfBC6ih84fFrTCQFhrtpOnnVKG3ED8pLpBDSyyvAjHBDm89soHMY8koWUigTjPUDhQi5lIXeGNk4RJ0g1xt0No6pU5c3TVcsd72Gmmz/gK5BSRr7SRQECQtplAZhGHtk51g8CvwwyyLKeMQ4ZQmq7NFl9AU5QRLHaZRQnrGEB3hoZKWhH1EaZAlN4yBlLHam4WIJWmMteyK2cMjyupPFycez/nFTHUhtI5X+UbR66CwQgpG01DtjDTPXmSB/UOsKRhrHOm0gP18126XLXOBUv9q19oh1aLX+samajnQm0AgFxufKPa2M8XQvRa0MtRKjDqN0z2cZtxL2uXJPK1VJ5VwbI2dT1IxOZmRPDAGVG/zug6/EChAPHhmU1M+nD8TN+Rgqcwd+GeoVNs4xcvY62W3pnM+uYW5+Dp2CygFLYW2HZujJhUGws2UdKSCXNX46xpgSYcr1GzrgqAWsO5gcd23nEma5J+C9Rp7PJieMDz36mmucHxiPNrGY9tbYWgvvWW9CrchrnB6VRwqhDds0UgU1YJdpCw411NDJfJ8m4RnTaG8YrZq5NNsPmsbOjGk6jGeOgkf+R/HDaWgGTLsRSPHZiBOxwxFyHLJV+KIpJtuj5crOmlrimDyLzJysxRZ70ryJVd9Ug4ZljglVz5tcaDtOnYPTdKDUyOIZlmTmbYce8cC8lXILh+b7+FA64FlvEDYK+t42nT5uL6Gw6rYUOG1aFyXOYDDa7WyfpEmLcdvW3ucNkeaKYsqzxbndmzthn168F7aosby3vU8WRJDvyPbPe9yn9z0y+6Cg5aAsIg7V8W4cw0mJT9vnkI1/KzE9KjC9YYHpjRN8nKK8qWuhCqJEjeynU8BGkzSXFxEUgXycJsGcV0Rwg4bJv2bQk/iy7Qa1XomNctZGG59P79HB/5bnk1b6fJpPO+nTiX5Zlj1og/swsKA/i5NPNdoX1uFDqL6CrWYjXO/+NTT6wc+VbFtQuIwg5EERXCaIUASkkubzKQ4fUE2nwdLI3W8ZfYCqJKw0RrRskeWTnyS+9xI2eLgYjCCKW14F3fcEh4M9d2GazzBrstRYPOTjOMRbQfXkBRgVkxeXsqp8e+bJ0OUbUkgguKC8/1uhLiwnEagi36AX0MHaGjkXCsetcxB9sHZI/f7dupJ4+ZIDDMgVmNB8J/o7aj5//04pDcZKD8ajHjagHrkEeR+2sMYseqcp/eoB/BXdaXeyHgtVHnZLu2aY23u6Qh2utej0r2ZbIQZ0Z8xPUxpwGpvFKOJxFrvRiwsYC2MaRkmSRVGcJR652t80Jwg7yQsO2PUh6MeyKlxiSomIdcMgSwEtARV8lYssEyGLSpGnQR4moghY/sbh8UzB4L9t185tqR6L/HzdNQMOlYvT2X8UkrILgg3bBMd9HvDUbIpBGvMkiOOxxXyeZrgj4paYJlmaRsfB/Q8D4lBp9qWVvrU77DNl49fLFuVlyfO4gBjSIsuCKBcFjfJVJJjAHizejJ3b3UbhqJ8FnDFEZoSLLwt5ZAuHfUGjjDHOszjgQejgeoul+6Iuvd3a3bhys+Ol0v58jX+fD/8BUEsHCFYOyhJmBQAArw4AAFBLAQIUABQACAAIAD20Uzxu/uh62EUAAItGAAAvAAAAAAAAAAAAAAAAAAAAAAA5OGU4MTVlMGEyYmNhOTlhNDE1ZmFjODNjNDdhZDMxY1xLbGlwcGUtbmV1LmpwZ1BLAQIUABQACAAIAD20UzxXu2eKZwQAAPwEAAAxAAAAAAAAAAAAAAAAADVGAAA1Y2ZmMmM2ZGU2ZThkOTkzNWNhZDA1Y2I1YTFhZWJlZFxzcHJpbmdlci1uZXUuanBnUEsBAhQAFAAIAAgAPbRTPFYOyhJmBQAArw4AAAwAAAAAAAAAAAAAAAAA+0oAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAwADAPYAAACbUAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | <ggb_applet width="300" height="550" version="3.2" ggbBase64="UEsDBBQACAAIAD20UzwAAAAAAAAAAAAAAAAvAAAAOThlODE1ZTBhMmJjYTk5YTQxNWZhYzgzYzQ3YWQzMWNcS2xpcHBlLW5ldS5qcGecuGc4XF/497vHYBC9JIPR6yCim1EH0XuLGj+MEoIYnWhD1IzRayZIdEJCRIkkiC5atGiJTvQe0Z/8n+uUN+fFOefeb/a1173XWp/r3uv6fu99M3WzANDqaGhrACAiAAD9u4CbWUANICMlhZCSkEEgEHJyMgpKRirKW7comekZaBjZWDjY2VhgME5eUQFObhEeGExQFi4iJi4lJcUhgFRESCiISkpJ/M8kIHJycspblFAqKqgEF4xL4v9z3LQBdGQgI5AdGMQNENGBwHSgm06A498+SUD/O4D/I0BEYGISUggZOcWtfwkfaAEiEBhMRAwmISEm/jca9m8cIKYjoecSVyFlMHaAcGMYJbCpr8h4VGvbmUy+7/NKOvpEkVPcvgNlZuHjFxCEC0lJy8gikHJq99U1NLW0dUzNzB9YWFpZo52cXVwfubn7+vkHBAYFh0Q/i4mNi09ITEvPyMzKzsnNe11UXFJaVl5RWfe+/kNDY1Pzx68dnV3dPb19/aNj4xOTP6amZxaXlldW19Z/b2weHB4dn/w5/Xt2/j9cIAAM+j/j/5GL7h8XETExmBjyP1wgosD/SaAjJuESJ6VXMYY4YBi4JbBkjKqpr2rbyXkkTfaZHH2+U9zmlVrkO/gftP9N9v8OLOr/F9n/BfZ/c80AlGDQv+KB6QBlYLrOpfEjv35aDYBifaXoe276tnpSWGWt//XCu4s3mgLV5Czd34Sw7DDN1awVAOlhxsDzLRRGP1AZcKePuCB0Xz20xyb/T1Zt+FfLLK0/37BZfUYAzJ/D1nTXxMpz1ilWmv4e758ehDToa4xfDI+5UdnIkflK09feUULDdkd0pESYoIWHPl1Yioq3DfXWaSPBiWbL2P0ebyA5zLOWz8gsps9hHGv06yFf0rPsNFqmhOe7u8MNyuwfGAPXnJ6L2kEZVpYjw5I8GU8lMxtIPyfV9ymk8TKfqbKXXT7W1Q9m9jGKNIOxN+/9tZAnG6yLH+mUzbJX1Pe00RSazVXTFCLpJwqEI/ZsdPqYH/uMv7uf97muhwHELelBbJ+KWz9aKnzu/UMUgYZpVUN7FHDLZ2MCLWk2LWhWAlXnM1uPXvC52WmdYrNzg/M9udf0UzxgBcKVOytRp0Tfum0Cn+h/j1/DOYTS539VzevK5lQ+I+kIfj5f2LNlorUDM2m2bBeyGVC0ACPO0dLPRWbztUcNnJMCFiKqFZHnOKexxCa7Xm3+ACMekgQB7PxMdfQXBnov0b9Cvj1s7yJYEk14myS4n0GhPYarehIKFQLZotbKH1vcPvgJUzUliKaW5Inz9hPhoiTxRcr9dSXvE3WtBLD8uO4FBZMTI02o4ll10JPTttDfRYK70I9/dnpvABoV03YW296tzLnisPakG2DFfLRKkE4Q/sjHgQzJJAPFDvrJnoeaBj+lFPtYI6EBDjOsdupz42uJSfU25JmzeKXzuqJhXWppwUwo0Mn/pFhc0rydWbHSPG7mIw8pGp5BPzWRUU8VpaFVVUHzrqLzaXBbtTnDHUs8WefjSCF7wZ4P9wwCCr5+MPueXt41W2CtH3n6ZCj57y0KI3IYvdCZsaiHQsnwg8vfh59vhfst1ITIrsFVv222ZprclzHN7+NbxQr8eq2vqMkaVE1UdwwyXNZOCDqTUKonmLK8uA8nw9ljDLohqvo6soGAiYT2JSdHd7Uw7TQ7zWd+5LrUpf5P4NKNaMDwJ7SUC2BvLeFI3tBNUFlVKT7rMSsmop1ewJ4wLrayWRwWdzTuG3+4AZpR1OwukhnK2JJvf6YTkx/jLktfZMPsr80oc7K3GZSt9ZrYGK+lb58pKus8IfQHQ5R1HHzCOtktTop8IwLPzNiDd6vPTCcdQ0gvy8E+UnRzn9KUc1nfTTf5FJ8Mf1D82UACNXhK0Z+0ih+PFeFFiMyPnZRdVS6oN6sFO3h7AxtTLH8rTMNo3phKBwb3rQoxtFaAL88f8NcG1T7kewZef3a5a6B6yl124dxv0yfU1/Q6Pdo2tkLyqqR6EX0KeSm2kiZP4/VYR+rtXe0KRSm2ms2diBfC6qRi4Wh8ab3Hz22/8monU77O5Fbi5dEqN2uL4SdC2ChyMBuk2s+tVCjGdXHqsivO/Tfh9edxx4xGZ91HMkAZ9WCBGLYduf1Yb6abDC97ixwmKCDN+CY+tKl/BQ5OTBK9DbVNes75sGmTyumErVv+efDzcqMXOssVl+4fJhbz7lNO290h7wYq6wwGBiSj84N2jG2+JvuEVJim1PlxjobQzv7245rueJPDiUPXqLAJiz6Mkk4KiKYFKM0zstRY+UHfnIihlV3mZWSJXQltP0fjtb3MdxO48A8a6dMCiJDHFVaOJMW8bwdo+iXT58aKDe+q7nJF+5DcHR8YSZNrZN5JDETDVR578hI5+2uTXcMiv5bVO7u9pzWUdZkcMgQrFIRPmHwVaMzXqq0nizTfJFvO8y9CtOROYI5gF6Zn8WOZDqnF+gMbOPvE6nCqnmxO4wxUMX65tkr/9uQduia+Ji9xw8NxjdDaw/wmNvjom4rhXDoT2EFtYsWgXoXJXMcqbb+S6a/CI8Tb10WI8cQMQ/ZK7wDnTPamCjGa0coEKgWlp5N/xJqVABhGBzgpl3Uyfb83GdnMZW3gBj5KDNiFx+vJNsDDnxy6yf4p+bmnh1LLjxwN7ahm7d3TWFJOjAR+FY7ukvf2Fs9hxk0k75VJdWqvLfioSw72hF9JavEeD4ouGDy9ggPb65+5Zqezj4qiR2hKBe3F+6OUMihRQUPw2ezaUoLr7qiX8UTIhRHXRUb+p1FnQ4xxNEfhZYW2KkSKMl0QOciacVo+NEQd/jr5Z8FSIblP/nwmaxGPgpmS9Q0QOhp83xtaUE0kBVXn8QzHKXnJjUvW2xmb8+7AiII2NnTh5vIykjLe2jCQeUkCOmNJSVM5JjRKc9w2Fq5m3aIveB+OA0Vp79huBxx28nrQCadBz30n672cfwoOMYKTihKd0iRsz5ycXIl/3GfK7PVaq0kSu+9MkhnoYevfLXct7f44tyxJTTJ9JJN4zO8CQ7FnUhROkW5xe8txW+IVZ+iUor7TrxImNS1t/wfKoh2p5lmkWZMG1IdTx+175+Z/C259yxJISZTQKrPpvj/affGnAYbpOVtKd6zNmCzRMFYTg66cMP61vzAfuko0EK+nxFiwTF9+Tei72x1UvjzPSjXwKoewo3Qiy5TGuqpg8yzGLABMoEiaGImiXiZUsAnN3id2I1AytCMFfpUdGgkOLclRy5k95CpW3XwIhm+N57/O5ErC0pN2k4ob3L1Dl8Ck824RD1m2IXdmBKS/qw4EA5dFZeASszyV8ZVdxhcnKJT/mZVhWbUuWr5Fk2N68We7FzVm/p8yDcc/I/W7rYP9lKZkuAfDDnJrr35ozKl00Uplq+1tXz+bmJb2tkmeWLW5qyH8GKWqoIK/NlQ8Mp5RD/Rxvu/GXDuBvFSs/BHPH6U7G4CDsz+YkMe08Werj+fdOuO2pVE0hG6qS7OJxozHhvGYXAh7NmROAQEfnD9UiSq5rDg5WTjwv3rK+kmk2YQUSq0Zsrabb1iPFCI1QLHFuR/XbXzL7Vzs7vKZK+XGzB8xtjhBqvU/vx8xTVCakt7ON/6P/rivjEYSG23qOlYNJ346wg3T7ikRlEDnZafIGYG6HxHdK5Ci7SnRfVmILpH1HgYXuNtrBEZrCvxQ3NTfms9DKJYTiRUnEqWFFAyV9ihbExHWE4nVj6iPiwLkxmOCdwbZrXjwGUC097q/fDjEHRXX6i5DJAj65WLgjSih/twlhtXF/hYEdZZikktk3dMMIuQMMw6idci8urHxZuzwEsSCj5Bqf+tVyMNeTYE84Fn2cfHZBRGJfuaQb55R0BkmuZpIllu8M4D1UfEDE63QrOGaiBL0ps9rr5YUXvHKlPii1taQ32lL3WJY0r0C4o/rUFjB2MmbewxzM/PaDpSsZl1iwZY3AMW/t0JD7w2EKTQg4WYGd0ie48SHfScb06QEs1cRM2SOSltXQn+noZJFwoUzzWwYPJVhgG5QWFGiH81awh1kN8R9YrDWumMnmtiKBQJifJ/02ffXe/87uQ+sqqstz1q7K4OYvk+7G2/eXvPoa56wYAvYgVayJHViyvVbzPbvlGq9GXNH/UHOakm7WeWoIJ248NuHwibCd33CatDCTaHVh8dMT3U+N6K5RB6oInjYWmDjDTM103wxVmrw5Tm6vDK4EtbJ+CGHSdN/83RH7LKI9QL3KpmUfS+nFC/cM6Gn62MzDdQliGdNxK/fUXVjrE7v7HGKtJHOYXpWjb/x73aO3mYFBg9tX9nr1MVeFIec+1XVcu9bxZ9pSPim490Jcs+DebeJNHnfC+ENdQzrwUJVyJ20YO6CupbxQI1Psg8mezBAFq8X+fiVe+b4RkCpJi9wAwgOuvSP6lRiqVezFfYplj5w1rndHZp66T33ZaxX2Q7eJFj4eUDfAO2aNMJEipItOG3imc0z0RstZzaZYnry8MMduCcr21eVD5k2vK6w60yF21pluD21dqVM4xCKbpciSVvbnkwAG11vRtfC12nCr625YzOq7kn8XSFeiyey6LOLGl0il7fjXVatAZXzfaHx+nfVFRUYxmH/i8aUFpiMmPjZpPM4ldcy5/FucHXvPRZ9qdoYM7wl8fJstdPPT8lA6pK5qjdNa8mT6PIJM5y4scELwT3IW+uHVxu5KxjdFBpOinPioKjsdtLs4NNLt+IrpaYini9UYozNio/mnrLo939acczQyt04N6UtEEfCvmeBEUsv/kRCscMeJrnYduACg7K89fT72r1qIoch1GWFwur86VMjogSN8JN7+bk80nSC0yQqpR7JPO77IUeohC8jLc28pp8uV3aZjF8nYRVwISxo1WeHu0oZbZ+8UJtuSiPPsE2O5VfZpQJPulNmZGRyIW+lQIX8evtu9zd9e88fPJleNQi8t65iFdm/zJ3C4qjyI/AfC6m3sKCut3LcUVlCqQCXvnje0/fzR8UQ9ky1wZw/52PP6rA4Xy31Oh/xGWzbwoG5Xt09OyrBLJXx5Q096ryDxccB8RFvZsdvAOqQyQfpj9LcTbUDzFNSdGq35iJ0xr7MO9NmeXhlR7aEgRQjwOYit5jw/rjwG0D0Fq34bElonD5N6aZupb5Hl71gt3jfdM/o64+pPI1+Ubf9ZqPzMfmlryfsnRou9Hp91zy+tqrtnU1UPb6PH1y897l/l5fg+pZxTJsk9tGhdF5lZW18DUW+0F1vXX85/gmc0KqKQ/qeyfSslBYby7y3Z9nAN89q8TKa97sRoprG3T4qlxsy6U2Wq8sf8gejs21PFqtUtW9b2MQPPBZTiEIqVhnY2Ng4gZaSHp47gK7cHPCjJAHO99KClveXCuqZEhnsVr/fNoKY0PlO5mW9ytIU3aW4AQJTj5nKXT+YueDnQnFi2ielfKMxPjqMjgFHiQaGhduu8S5pghMq3OKntYlP/oTNFCnYCwtTnvLXx3xX5tVujoMaF6waSzWm63HiBYCCgiAKb8nevkFpAQcrYiOtQe5vYJ4V+lH79TmKF547v4zkNRnoaocN20yXG3K0P2oakcvHc72/ZpL4WHxAKTNCOg6OFBI1x1Vb6X+e6iBqS3pTxMzk3p6ltYIQmd0P/i03Jt2Eq+N5zZ1lu64YXOY22esgsieB9JDjzreAsctPlL4RvsPCnWPsxcqDcblmD9sSDcqZ3blD8VoYtyCjZJoS8fIRq67bPVe3rg7oN0a+JiEUz5mFMmUX5WzsiqMK8fFahTtExat9h/8/cQ46bGr68Vqd17R6tvw3GC2mO2wrZDBNOGg/NYYCdGv+oNJ6daLF8uPRRzsj9KverdG3VBHub1ytfw3OrYUO9+SpLqSPFrUzkihubaQuSHj2WxAz/B1hCrjau/6gYYRfy9TQKhVm4BY3MhU4YC5eL1phSbAqQjIPNxe7sTV5faknyxG3w2mEjD1fWbh2mkBpKRAoAoIEEgOIvgtNd1CoVobgISWoYupC00/tPVLA1fP3yMuKWEqfoBL6e1L5joTFuDEpS1QDNnmgE35cJvqSmTdhZeF4Bt5M2USlUwbGJXc/p16YJCfcKiOOqIMfbNRqJ0saw3cdBM5YVC1xpF0COZqmOh16uVLfTNZkxucLlsRSWidzpZPeWNL9tO3DHjEmJ3dMvlhjyFcHDSmfnyi8bbbdejcx5pR2O5ff35xLVTupZ57xuwP/2FF6gYGQ/oDy82R3t9RuLeUYqTwGt22Nu/37NvlzY5cFe+Kk6cHKVyGyBKwZiiwb2YcoEwL/SEcNiQ+Kxym4cuiQPt7y0faXblgNi+9KXM8nFT9PDMs+VywWI5o9lZRkj3TlzrKwesI7ZfB76M8NgGXoWU2UdRnfabNbV8h/vGJYyjm+mnag/0bIWpr15zDzE/d3Sf6t/c5kRNgm2f9KJJxTl86YNAEce1OVcSdxym0eX/D42BMVOl7JF4UIc4WCF/jPV1sPGHgXOvGVEPn43nN/Jj1KndkQ0K8a60KVNoWTpffpglHr+tRlgy/x0NRIBPsEWUM8KDs1dj/zrXfdjqEoUXA7BJds/Vax/s9ILrMjxbwMsKpZTR6TeDg7vXOBeC7c0eDjq4N+5sDdiIISgWxPXz9CN9O2/sEdaHJCg1AGcrhxiec2j3P0Tk9NrfG8Am5PVEb8l57bqk33t9yjKMP5lcbEf3T0F6k9AfJPqD5lDUpEfhP6ojVk/o6aNIKi1ctRg6PFaMWT8Vek3AxY5K6I/c5sU/OCINum/LqNeh7ZmkAQCB98yjlRcW9GHk1tpmHxOEwYYtRMAxfyKXbwkVuquK+flLU+EE8kiTs57flrYvkrx9lxsB0AEcKlVeoMFN3YWGETxTG+LroHa1odrFYo5bd/J6VrWFw59y3HqTu9khG9ipusNumwLt9ZXrqRifKNwrcVY5wiRVSJRZUHxK6+9NTKOvjuk5JQz34fMQOhzyfrhCqarGaDmuKX3R/FvNPLq0fWOweFvFZRK0TiBV+T1vFyY5I4NBDiSGAVIPq83O0Ut2bLMJpSkP3rRT6qx66+eMGvlMtg59Py0YY2ARsJBzZVSs58j2AY1DN5rY2xo+Kv74YRZeAzv6UX9SspIPb6Nv1P/lIl4R6+f0c9FVHLv1LoWQH7wPZC2gWNbR9BMohXeMbL2vS/JspG4u2na1gaILbtEj4vQyN9BzFE1gUJXmE4lqKMgLycj3WbDWFIjEsdRuwNUnFtJJcABqQhOHQJP7AQy9FftZeOGFL8zXdEIPhJgZwWAhF/SneZ+9ONiNajC9pMM2SNEFePiDzioIWZBttUGndqgqQc6pTcgQKBV8jiIxkYQDNZZLJAFEJj/YCyR8GIdDtr2I24mvxqQ+W0G8Xeaheh4+3ooWK2Gk9JvhAmpJuzIqHAZSMoprLTZf5MJAQZlhPQPbdcoPYfZ5i4kuosJoXaLP8KouP5KfWqmP8Prycx0xCkXKpWMEMrbu0rexmb+yeDd+8bNGSp2vwZ28ZTM2dB40QQlSj3nY+EGL58pYXTN00C+Mex9miAn9RAa+3DXWZWum4c1GdAX01Nr8mLnMJS9BYaegOwVMgrdlLL7szMxiq2cKDN1p/GWt0iiG6/GnYvTidbEXqYfOBfifNjQJeOLzdacuXSTWqwGtsQU/pvjNbxjRu9+d7brXaqRi0+qF9eXDdvPfQ806gt6tODx5bvs/iWcetQ0c8RcqNw+tO7032rzQT57N+F7DSL1rR23i7GWW0XV5WZ1R++dj9LUfWjIL/C4K6l/T3ZvufETyTvv19MXoEaF9lz5VlNY3lX9oHyXRAJkiQ2iMntNmKJyueBGI38P3OtVHZc+YO+C955H5DzhJZy04v9hOvUP09q81xZGVVnbVgaNogl7uu7m98s1X3/QPDJ4pDcBNxI0zcFwXNUFQjwtmsC3uL6waSXTZRA6bPur694uKjnTsuhlPm5eyb7aEdqikNx89Cdkhx65HreicTxicL2Y2t66hwPDjUD8/ZvQuuN0ncIZALelxu/AgxAbadv9Y7iTlZqBP04D+YbhO4pUMqGYMI3OxOB8PZ2JHRHPwXm17sLBzvRD3jLjQymIXgZcI5YKnikGMG1uVBemBLbWMh4DUYLKOsYyLr6gxlEfAJpSjgdg6E96wZOILLl/OPIHUSpMBUCiVCOUZTIBdIwc8b1tIbfVJ7k+EO32gvJGdOaFs4vTMovK2nNAtr/LBFA3TudT02IVIsCddxQlWQU+vy6DfLJ1qoXFmmQV4UQYiNDo6cmTCS+qakbgzzO6RCC73DIIw8j8Md8FDfhTQ5rUw8zE0hRy0sRHt9JDyU8ZdC7JUEM4cIqblilCJ2PyxsoaZKErMhKjVJQMrTgfScj+d0Y2ckpFFWU+wkU+c/CgyrnxboN13XIe5Ds46CJlO6/kACFyw6evDeL3GOjd9ojxOzXC9kq21K+cfe3ItbzIaZGc4IFjzQelq+LGMKSD7pCsccdaJwk0oAB33MpmMUk0qEM30lD9rCV21w8xbzLN9C0jl03fl/35FdKN4qsT2HCKvH3eF0U1DFQJK5QQIGC4E4GDgbey4KKVCO+1tpPEpXjeDFFUbNRuAnfyl40Aie5LtyyBhgVdg14pt5LI22PktAV4ygsz6Uj3WA2+iMkfp7XIztDSIx/o5pmQEeUPJS9bcFQ45qxrjikb3H3Y+Lp1Pfm20JkwTyiNAKs75R79isbrPPz1Lqol+j+XLXd4njLuHVX7pd8/IyLq+lpZE2EuiX7n+3gYJPZyOHQvPLy6ObxD4dJNdyL8YCrAHPl+zl3yU9Fjl3RX5ehl2dVdLXYFKEYuyk2d/kXn8f0RfAS2opuAlOURy7bPcM5hENUlbg6S7fMQWKsbvFUB5DF9NJ+j1KI3Yp3htxxnb/qgXDemjpx0tyFGbvvm2f3KFALY5w5/fmu0J0t41xzvodn3Y9Ah8KfCCeDMpY9HOJ9ivDd/g5kubWhWMWQouJG5JmSZTt4rb1SX0LGRyLM4oNOI7uvBxCnIaTZWqL6rXbaply5yy7rP963DMPdPW5kLby2u1ub9Z4ujow1yplSkaQgnoKl0opuFRNFcqZNdgw/L0wM8s8oRqbapLRFtBjHGGl0rxz6GhqhiaOClT4/Av119JHscUfZpBKu3IhzkF6GHiN8NKeRVDupqqBLcCRpSKreWZ/HvuLGAFjUPF4pLjGhxN/OTFygkZEsxTmBT4NGj0WVwpsRvaVVx2ULNJ2WBccPYi/LoUBVJPCfAVzsVVwvSCBdx2DJh1TcwOiF1pBhmbUjS7hXfs76ZwQ7gERsDArcjRJvHJNCzIDYbgAdFI8OZsztBDbWzClbfswIsfWH7Hex+YSFHekBoR17zmGoQixhxVUpw2sFkzomX6sTQCvWGeYGzEW91IgQCghaf7uuYjJ1Fvef3phVcPtsstEj0BQxW5NUG0Ut58J6iv69gWdMw6Mp7+FKcceFJCIWBSnJviqckQaQZdVFvFbfadFgDyt5Ken47VOTy1FJIXatnT2dP4EW93IoKmN7oXtbOkP9FoPpwIntcmLzYwly9oedNYjzH30y22FCGp6TabW2jlbfvoA8iz47bn2Vub3v6UjL8ONfX3VSZXdhaipZF6XvM/9YNptKuGLGBpv/4YPUToCrwMjv7buvZb5L8jA0QvjfGqBxqJRKLoE1xNbw3wcesiKOZEXgL27ptrp8ayBlTujyD+VFNQt0c5mvT0AlhOt+kZCc078FKpw+Wg5/O3+ASNRo4tfonc83/KDbi9iUVEsknlbIXoQhFxNmysakC8p4s1KhP1i/NSLWK8psKbs7OGSNFOEWIZ1p2BGXtHjb+ve9Wvd6bQ8KdBCWwN30yaoE4mK6eZzpfv8rm7HR/K/Qhfq2ijbGLUuZ0Lg02+QafcWAOB4wT16eWHEyOs8Efd9YEEupm2K2VJhK+UN8VXtTUeOxCthQKoqsceEJpz9RWaJU2vQKhees2y3euN1Gowi9B6FXsRP9pD+nYpDLeIj142/E6lxh3fa63KD5+Zm6sU6dPy+sNS5UdcCxnCTIdgXfPcI4S+mnu2BW2bNZknFx/1B2lT7F4Gpz5GdmWa3fNAxXtSKlTwOTGSTK9D+zzjctvftA5TPzUE+3/nPVwm2VKGrEMBMvu2gL+eqsareCHwwtLUX9kPyCr1LePygdHbIcPejvUK4vX8RyYp+Z83VyzNbjw0crHrDIrAHjuUvJYS/0CALzdncoEHmFGBYgKprmhJzifLeFp0qLi9wk+8qXVndxdPZXuy+p9eGqpGpeHNaPtFELaSrdPvBfNuWK5CdU6dbMUTVtGgc9BsdEb9t48x6ptazB8nwFf7bz4JciYS9iMVllEFC4vUaIyysBV8gadCuR2/Oz8n/7hff3GBoHyJ+4x++v2NN8LZYkG7/tXfbTQFIzh5dTKtp7fRXGAjjA0Miez/w6NwAdZDTuzIb4dAF/nMRP6ha5/RahXCLoOOBDdqooRG9IDP57oOVk4k1KtpUIFETKO416oxbQk6/nu7U3Rr63cnQCbEFdt4n0QJFm7J+pEOzepEI0YqRnzRx6o8JJnT40IWoisUJKG09elZ49g4ktlzOXP4fta3XJhkPpO4+6ScQZmDUHtIeUdbz2SZd6EOfjEVy86enHxeRRqF7oBmEtkl+iECzaoTTdBfdGIX/+NUN6h0jSjVCguvqGIlhU0JqWvhJMAqB4vQuW0MBp/dQooPK91lELD9Ot2UQPTL0wjvJgKOTHt2nLc/k0MXrZgU/5jxVs3vjKkN7xBsyLm34qJM63zWquUPH+pdgl1aH9e24uXE0uel9DB4PzL6OqUqJBMpkgE7I5na1UKt7prowQP8dK3AB++W5pkk/aVsCGKNnFFnPdqoykDPwy/3OsSLGg54Ayg0kHr69NLzfnu6+LTWu1vxZFuTTmLLGxSie5bJPfeoAs4pNhYGxljSETn30rfhVS+oP5WCFCjjCcwxHEbEr4IZedHW46WyOzmGsDwxGWjwSOKkysBnTqkGjcu+EQ2zduPz0eX1UCiwk70Q92mWI+9uIKlY3zf00MJlj1OfbyGAQh7VXWCtOtvfez47+xIOda+vc47MYz7/CzWG//aB6vKbLAd8/YG1J+Xz+bfPinqPKMnKrt0QRwZss+b533H4MKLz/CbzLu1MHGqVM4dS4S+abCny8Lpu0+CN9cM1AGJW89xBS/dtpsfDfthRva4fvwKgCWyi55Ps4rf2iMYo9KedhH8DBONs7DvCx2aLYAv4NWj0p4NKNjFITDIdVeHVJOALNV8tvDN7pWLLLyFqwtaGlvEZ+UQSjVD8TeCdOY9tRqZXNSzowsccwf5KBC5YpDYhRy6T3x4et8gH3HpLiai0tlPR9K91DXNPN1B+fQrRRFjA43lyHvSoivUa4Zew3UX8dYmO4wln18WxseQBU1gPktruNi65Bz9FtdTO9CohA/NayT9ByGS+0JsddTPYrlYestzSReSdFAEJspJH/m6glHVMhcNlHP6x0XqmVEemOi5FzyFlaYcP4L6XkKNZgWgS9uFu4EJjTqVhzP2n2HeS8NZeu3mT2m+Dbx6w+h6qwnasmokAmb+E61ouUyYQILbXf5z6YVJ7/iGdTyY8xIvpvsy7gaxbjjEkq8RMejISSvEWh1hRKAv+KApF4fSC3XV8ysRGL+jsVzqQGYeYVE0dtQcjar5NH0CgUxxYQ9Q8dXX34joT067lm2NUSJAMYrJGYdHBjiyvo+6ctZ2YrEDlftDwWMfg9lGWSMFHurDzlkGJqoyuD1HyVkUV+EcQdppKgvkBNQ0b0QQadHTv5kUQGd4taXFi3ou2PELCZJMHni3UkvuYNiOHs1VZnaZOZjK2XQMuepEC5tuDPSFbCORIAPSv/T+yFGAGeul4ROfFD8cyxazu6OuOZpujjQfprx6DDcCmTwWVFY3D8nMiF7jSvcXkj4p++A5cSrWx86Kvjznr2Yyvfze7DJuCOAZHP7kf2uTYuysLyvZ7R5ueYTVqG8Njq/edD848enZXfbIOW2J69M0kOShmtbqeuSvG32Xu2MVtrOkdeI4fp7XqemWyZe67wXFvdqYns8LpX0tIPn6/5Unxvrz3qbfBf9Gt4eF86JizsfIdKeBiKMsfMQro8wfNlkufXsIOMg5m59lMyTT+YNH/xq51ScxdJGL+5QLn769gyv1cZW26icymTyhMHdx7BO33rIo8GM1Uz8bYMlu9CyfrGAsR9/1tBxzqSN292iVLBImqjPl1e+vVW+bnlCs+rrbAbwr0AXm6p8yGEzh87q2qQX+wPX3J/vsfWRVcdgrOafD70aDtyZ3TJNZ60UTWOJ3OZOf2RGf7GJ3gCDoy5ic5RLLlxTB8ONIcMtpgrBYSrOFAa3LQTe8k7e0hryZkzukYrGR9X00QWcivQykbf/95fq/tT17V6l+iFtjn6COF77snwkJI4zRV8f5iGT1kQ1kk9yn9EfWUWmhHrbnP1umMnYgq/ljifPg4vKGohp3qiGOYQk5FRAOiU3YEVMoByWJrR0v+zZXcLKv9NOmzCMZKGYtXQSENiNPkJPuZTpCeOwhABopTGncXPjW7Z4TrNWOIlaCmbM05/Xp8Ey6DBYSKkQo3eoMSk/NhVtVBGaNi0EKXVLg6M/0rYF9lbxYvDqyltGjaVuLBo9nLDAYeZy7TQJGzBPYZf0SjoEYRSCc8HeZuwlNX+niTHULmDmixv3jtApjNLIIWljGxLSSF6bXltNRhkI0jkZsBI3LhLMovRoJViVJggNA9TaCoFlTH4eDdpKUUmkjzVFvFqDY5Vh4YzrGfZEs+8vVeteO0aSEKfOfnik1qB2atgqBUyDuZQDIS0whvPR28BO0JDhF19TWpp9/CeKxEAKzMq7JyYhJqBXP1Jrf/wWlCARKgpU1EC9KkoHxff2OOgdFgu37l645FC79fkE1F7X93gsgnhm8uy84mc/E1Kxev6ZvUKGdr4o29Tnnguie5guTmfi21A2pYy2UWHgMHqbRKFoXajwoL1QLdzMscsoepixZybcD4Zvcbu2WwD79+io67cKEucHDfnqER+hyaglemahpQvaYwC+iLGKeYhM3vA/dxXmBwjR8AwyJxZ8foVUQ6pIuTeUpI395WNW03E7i4h7p954oihh5VD30ermPLLevgfhX+bMyID/MtIgaDvYo+LdpwaBD3gTgxZx+2f2QZDEpAJC5pzMOoQ/g1a7F3adsRr/jhfOU6r/+DXPA6VbUUYajG8VVdbqlab6aFV4mCC7O1fuGc6vkHqklxs+hgIVxdO6jl/tBLJmO+qf7QOgCPYboFpGNxlhLyTIFhfiM1PEXaCosis+WvpQkRf30banrY9a9doKqZx5Z/u2ZI+dDaO9K/OgNq8NrIpJWS3vkd2jJstUBm9WDZofTF5Qr6l3sYp/mRVpjirt6cakTiRAHbSKoBLvWt6azfVQ97IRQY7+gj/Pfcput4nvNd0ASRbg1pAgCJTnqAj1HjbqhMWTGHJM95IkDF98oK+dbfymtmvBn6mxdtESFlmaRqXrQuaEQqdKyEvaX9dPaGq2c8RzLh++8izxoIVGz3FV3XI/WEj9G22tTsdPR+k1Q72gHNNaYh0TSLvCNOzb7U7p+eRLTJwAz/l4WyrU7OSi5GOYuE3beq7nwwAHb+RWpL4OXia0p/yE0xzT6qXFc276nB4wgVLnbEfI/daUSgjt/Y4y5gk4M5Uq3j3L8FKkPu3hUDEiTfdidUOeIq7gC2BCXeoswXzqRVS3mYOqJ3vR3b8MGuP9cV5XNG8XtXoxmTDqzyHX0DKPUKcq4KkkuyDtZILk/PzYYalE552k55tu3dIp6IEhuR13XBftFpn/MLK9S4xsUrDP3xEzywbfNiPEDJKqhu92sSfCkwgLewA7GdtvUi1eCq0pFOxQXQ4JmltSdwz6mlowWlX3TysVvA0MpVaSKHCueG+b6D3UbWutUyJTgdKrz8rW4Z1QUCR7oviZudoYpZn4pvb6uWn6ajKppgM+8gjFIE//23yVeecSUZrK3CvkY6hA4d4f08saTYfzuxwOeSwyGwQLwT+6lTgFFs7uAfPcABNaC0S0JwqRhvzPzNSy55rZMsabHnDc20Mu+HcBAlm0wh7IvZkULeK4PeApQ14wMZczquzqjalOKfksc0+oEVeL5SFo5XiQFUoUmEJjnGgbOS/iMefHG+nm/W1SydDAR1lHFLAS08wlHMMoTVbg7R6Y0aIA4kU8K9uGSVjuN/DsniOW4Ftsf9n8JARXzlNYgaXEfsWxZ0RSG0ja3R12fv2x592Kk1mstkymqJbCkQHPUXGZ97sRKsXwjEKXDOdgRor2prdvBRgP38glY7R/pA4iokJGmx9AVc7zVHqklj5vIEqFgSF4f/DKKKC40U8quYWippSjNHkLectYcO8DKBbz41eeKrsNDnQ+Hr8api4mUVCCoDU0tWDs86jPlqxMea8FKd306fX2GSLfSs/DBiuPjHX4EnbZ2qVfS3o0skZCBrS3roOrxFNbeVN+YivpmnlW/wt1rOFJj50J2va9ASarX6P5HxpHMmfPI9sKcQ3b+bndkv8KXVzT36bexxbJGV6/4ORM1cZTl69s9DiIcFgr9rBVzBzcdCsqwlqD/sQcccqd+bDjHnH69VNTmzXmVS2FBXBeHSlTxntSAeabf1B0NHw0C4Y8RxWpGYIPF0BjjqOS3bvUBgvIPp4zDCo+IJqrt6diljCa1LYAb98zDe43FdoOuAHoX873rqXItQrsRbQkj4wQ30/z9mmGLufhip4Q50NI3pGGf3AlyWCr7GhUoEh2o1BJMg9LEjuGlpohKUlJMY08HNgKKxfe2/YQz4pEUo1wVdT1nlSsmZ5XSuly99qta0Yy8xjb1Rxxts/wKkrm9UdKzyJ0AoxoOyOfetm7Ba/Qi8+CpWzJVYVFVX5B9Iiartxk6DIpNSKeX7oruMZoCFTMNF2b7f+yM4tFE84dU9o4UZZcCLbe9lK0N6gIqvh3qaAp1nG4beOIZtzsnjJncOR6IXMpcQtDKWTEfkSiiDgDjKfzJnlg8h9lnTinffRMRoM2a13rNu4IdZs43ifkInUy53OvK3ulhlArZyZfDvoHRwm7Y3n7vajgLsBStDO1+Y7yr389FLrfjBLpsElIXjUOTmQF3rK3Xn/8TzI0iVDORuEnZUnt6h7d1nUPXFgi5CahHhSo2E42rOP1PS9YyjXPkVbwn6yiastZrfp2yZZy/5pmHI18974DkbJPLkEATxNprNWgP+Fi4oPId/oCIY9SScmXCIwMG6hNN3Ecgd39magEgvGVRcXVI2P8+Gdkz+qDBHSkHdw7bhP+ahxff7BZvFafKOnhbQTwcrStlajb0aj9Nb0DhM5irtz1cR2gxNMTpkoNH6c+KOfuqmK3u3k8TSp5T6EjiWr8srwNYhNUBdTbEz31bXlV/RrH26VK/Iz2RYuXV0SJXu+cQx15r3ydW+XDWMZl5STQShLp4VVIhfLkBw2RFMmCzD6A0p5wA/xrsEDt3yK197CXN8D5cZTlUeycb6+8PqdfH9Aw6i1WWp7KtILOmCnO/8Txg/9lFkewbcEel11EJhdxenP32HSGd8RLBWFhJ3lQ8qIP6FLOBNR/K63ty1Ov//lfr+nY3/Fyfi9fcVMpcI8kOqIJsknqFjqN8hlDLhdRoo9KiYqduquFso/nIMolWk7xMnMEPKaF00yXE5K5fjHd9u+hLRPS4wrqGMkekOITSLkOHRRzlIEEDOyHm+pTmAcJQE+G4N+4yPvTfwekX77XAhllQcOmFdMLVtW09hc5BsDMc500o7gqEokYh/SXHf/k1rgc5+rY8Kv1Xog94sv+Q0KmYqTyWLWcBDO2vQ+2iNF7ICSB9qCOiRxezwtXywdsj9ph16VYGs+SKGwqfq5gVZ81U3u2wPPzl+LR13U4ba6eOt+z4zI6unbYfkQcPzbz5aEEU9MwuLy0qrODy/LdJib6pEtvNjAFnIqXIOOI4dZ+51TEgMP0FqpJBFKu1IjdAl9LfS1G79IGQf+7/qzlBGUdF1V002227QYvl2XpHJz0FZINCL7RFRLsMWpdgBP7CNPX0ZaVkkbku12kMiaVGPrzig8vJ6+r7kCUHGzxOZDzPFF52EEbjONrHkYHyn4cJyC9yL5Mi0tU6THV0RD/hVtuXNcH/g44cwR7Tp1hxpSOady9IqYHRRcQ3Om02wRTbUUfuBrlAcHEnt4AHslOaiCuBbX3K1bKHR43xrlCCkqkuKaHveA+iHX24+8F1rbrHx4+61NeMItkLwbtaeODYUYhx5dJtsZUyZeYPQPjYcNOliTUJs26YTtPCuLysRnuBZ9x9JEk3VzY3papsNCXO2UNmkdt5XcUp1J3upVfGjJ3hC1vg3puAOuGRIl0dpgrgjWoXSiig6Pa2gzd73BxiafhUHVvIqYnVdnDCxmK9CoHvard9Pk3sdM3YtGfb/Fzyv0RcuZghe5iNLMF6WvKypaAfIIgOnm/xIqnV+M3BNl+3VylqyajdUDC1Wnz493eefKWCbGIBE83ktPXOCaZgskMH2RFdkXD+EMwSHABHweEF+Y58oMSvADoDmFswupO6TI+4OBys3WGGM18Lzq/GH1UQp0c5ej5E5MSkQlo2Yn57IhihlR6/posQpjPDP/dmHmK4WIO8yRCOCTBN4CKNCx9Ma7fylAD9DBCAf+IzlU4RXxsPOLkt/ODtp5+TWnbpnauZEXx9mu/BGEvcae9E5r2QnKseVhuH3g3RZ2e2IU5BvFbB5yIW8FpWWVzSPQmfjvHXdf/zqn0MmLSROX0rKLoiXp2s8DlMysRcjiZ0a8Pp/YyEdd+04Ya8nVy6H+eQU87S53PyT4kbG4pJ+H+AYnAAKp5YeEG4NHRc6bAq3T7DqqsI/xZX0bMqCWvXzOuH335m3qNi1e5jJSifEpiUqJlvhVFTbNcsGHgRtZuzswDEBVHiBt5ZeZ4gUALjKY3wA/GP3xGsQ49nt+G1xOBjP7OXUQvDE4SYf0kbzdXHHYOTjXuphD0eVO8TkmbntyWqjb0SVgKG6cKIC/JCiFZLhdVbduslxgDvolbQjsKrmUcmeprgt73XZFbW+c3gI6pBPfubPQ88383wENAKOtnL6RxQPLySAudUus0Q6MqmbwCTxwW+Gk5PyeGKKHUfTn6zGthKRI599YaOeSD2dBOASB51HP7jztrd6iHvep997RTggZh+erC1EtYfMi11Dbdj1R9qq3zA5RXRKnblAXbcaHXrtst6vWj4j6wAt32o3e2Ep0+kB9SL1AraKWmEoXTtqKykGL9joOSb65RZKfFvejZA0bBs3gIT6v06/sNisGb4vill1jculR75p+e8pI2Z4AuuUb4frxHQATHqwrGNB/IqnHkgj17flXBZL7E1HKBl9D3F/yUViHwk+WCoeIHxGxtK36I4ePKxeSfXjQj4y1fU9NQim291SaSqR7BT4N4OZ5cfxb6QsaK5T3oFmL07OvgiRRPCb7251zxopcEvL3B6JPBR7hc4dIfAhJV6PLsxkuKkqNcMVnJ6OnaggEzLauEW5wZ6NKI7lgUYMXpQ2P03cv6vYx+pmBgJe6EpMOEoZEL7QjBXDMzxmf1F3Pfa0KZXduaRTn17GYUeCwkOrLwCqzQA2E/oIU6bbDS7UCNLmkcrvBtXn7zzNdMaCbPAFLxz79PrxoVPUiiS7Tgmv5yvj+Pg3Ie7q358J8UqWnupURa5QQIwCKWWyeLvFU44ZQROHGObHcgezAh22FOa/sO9MqtLuovmhUBSxqghhs38rNNvx/eQ3ZRQqBcmJ/KVy45tzLj6YuL2Ee5en67xWqKEL1Cj+c4cfSO93NQmv/EbsyfjTHr/ttDAmbkthEVIN3/hPULSvMgimYN7jtMWRwg//5y8+6okgVw77WM+Plo3Rc12I7drKzrAbER+PKHiHGRSBim6d95p2hGCH7ZjInIFCcQg+lSQuyZesYw1/WvVdK+2D47pyW7FFcl0mYUA8rRmxHnJ6yqa6j++KlNqGPqSGq7H/iiuuWYu8jMe04G2FtZ5jkqJA/9kCzvcN/3B9QObh7oJJUUGb7ZegPYFbnMKP+wv0gr4qgWE9LNpNo1kA0vNCJ+Q+Fp1IW9/kOtlOGU1V9XA6EsOzspn+ETT5qy/xJ96Wac6U33R3Abqdw7AqBSaHUkTwQoDFdVe1W4SmI0HVbFSr4i52TSf2D0OMZN3qTRPUs0xW8Jvf2tD/jOYm8ARMmmnKmP7xC88yLcfGnqjxfnTh+j04h38CAXp+ktfG/vVl7A2LjZ0xasIUTK0oIJf6dgVUuMBjAyFMiDoFQg+Rmjt54TMKld8PbfkHUt7+AuqClOcNDk/rsZzIjpGRQxKJlK2L20kFp1mFreSn2Q4BHIM5ZnF7J+PCgrEiIote/z1HWmmr7HXvn9U4xuuz3NcqoW5rfvZmlU8HoAJKRYhbtmciFF8axCooMq6XNjyHjoMlCD6RVgXBXVItEm9h2K0JlUcvERIYEQIg23DO3uRP4MYRi0UInScjj2ElL7bAR0RnyOPmMXNnPqi1QszeDQ4LwBlA8q1BTQzD83ssBnEy5oqAkDPtzZsexQweRDt1i7k0lES1TZ/qAJV3pF8C1QS4TfRs+izjCPvcIjyIX+2BETQ11qQd1ZfosZ6dUj1ZZG4lQaVShdckeqXpb2e7d+MRN5L06OyWLzUPr+Z/nPxPmr0tolZMXYztHHZQlQgiv7nEsOTfcvEA+bb8vZiJlcGozpv7ATaMrKIvXeKfLar108NO1Ce9sCckT8r/htDnqVYaTebvG8Fnx8yGPxquvPbuYl/1LkEdf0hdeEUWZbMUqdBuVonwhbI6K9FH/xxtafZU/SvWfKf7UkrGVLyuH0kYgh8uuivCRr9V5MNptkdMEQlkGyQRYqhrpe0+fMRvC9Pp0rISv/4upD3A/aGho7Z2Geke58FdkNlgCfjxBHaWDqHV7AIs+UMzXMEkgVBtZxNlkceCoZmaTsSF6eKZd8tSZiDbN7XuSQA9JIdrMGH2j+DdBxuXFfT8LoIw79nqZaw/lXEYZH+Vcy9Nrsq4kMiTH0FFRbMBrJd8h27cz57nc/xXVuCbDT4Yn+GUuqLIS1dapteIla9jNZ50hlciibbzxNo5bTKh6Rv/VNcMr2z8WVMjWV1D/L9LEZsfn9Nkd/7keBLUY9VDurFn8mUzw3Zx8+uPfaEWupHMB4bIT8TSKQw/Suk10OD/kND1yB4WiMfAe5Dqd9vqojtwdaSwDfruQyxlwpwjr2jAW4Afg/PWXv6nFMhyrSLOpQQzhHF2SFtM5HiDwVz0ooNd8uozhDjDDj7ELPutq2IsMzmoZ5lJOkCH8YSYGTtjIH2wBv+Wgd6LkJe3SeQUikUv0oXzIve7hDgQ5ouHVDv295fKznCxmTG/1Us+LRmdEtb4jtDfC0WkC+aXhdY03BT2CmgktGp7oA/VsdnD6L3NHro5rw3RXX0RV2zozKXyat5mYW1iJjhvL8SLTdL9HlKPKBV3DOgDA7Kery3py0mG1kNd0LPm2+X+EO2AkrTWU794ezkUbJyX8MInLLQSikKOlTXxPEzDPgoSHn8vmD+L50Hrr07K0xZ6FvrKuSrCH4pLxny/Z9y+/pCn4wunqf4ReUE9/E9mFVCBV6J72IG4DCfK7tfUt+EF1dXg22WXxIZZdF5J+DC5hWE0tToNnz4M5J6NAoroo1eXoD4AX7G1Tf2ZMi7SPUBjXTekj66eaola3NrP7LytHS1O9VLrAmcUSZgjQYeMq7FBvtqX4vBPC6VEGxvikoNh2ZCNV66JwP71xz7zzFv/6SMgMo3tN/dgP4LXOUcM9x+lQI1woAWhqQZePgWAXPYQEOXo/Ia7DUnqw3XNgDUga7vk9BbCUiEa7K2kya8xYq/2no6W7vdcbX3oQjefRVebJyltuBlphCo+/cwkq4RiTskIeu1e2UHpSHhuvtSAjdAGOyg5S8LividquY5G/lxYJayyEHuAWO/UJikRpEaOOFuwoHHp7axa0VEYxk3jiNO2Ryc3ROrtJqVbnS11zR5KaLsmiyJ+NYVG/z5YlpO7oDY9c8rNweFXZ+/exip/2yh0m0NxuglnPW5jkelP5up6QlPCyiXegI1wttK99F9V7+ZrgP285SDc+1dtdkZnXMU85+nZ5oPmcGofhVYiZ2bsSLHEfwP7p1z3Zny4izwUL4wzg+Vz5CNGO/I5LbfB0QYioZaImUFAO8m7fOjcS7Pg2QaHiH0G5G6OWZB+BW7/PgQg8lOHopzXQvbaJdYVlq6WcUjxC8cIed09ZcRrJuZhdOX3wTY1x0D3c6ydO1GGQveF96depEVL6wD5Jney6mrOOGPL8wIt3VRp6bvNtVDgixZ/HmPQGSMXozISfFnK6lVPK2otq/ooDhEtXVH6xiYRvtBV4B60oZZ5Y12nt5NHaQLX1K+QoO6yDjvyFjqqC+Nq8wKgSBMtN2PNzq58up80RvxHKUYpIJL8Z2MTv51SsOnhQ16sLTQrwctbwxtkdd2bpYl4+XCcaQOpuqJYNXcsBHjsJ5T57051PvdsW1QqvpuWrDWqhzoVKrPArp/6zHHWShzM+2LPjYGmsFvS0CNV8DuqR6hJva1V20orkQgR9UaRRv+3NsJ7WZfCxVevQwYkE+6wVLB6HqPvQgtf0689Fgmqh45kyYKoyjNy/ISi6WKr/LJ+KlWIwLt1Zf22I65LC0ZnDxRRRySCwi05i3uZshHNGOgF49uqgMdAL9kpk+G5XyfNfwH5uGTMEa3OQBEKUh55NzrZGTsyigGmvL/iKy7wqjzSVC7eQlT9d75SYGEGthQ3D7ypLX0rKZCs+b1RA8PMQRchZ0pAuD/XDIhE5BtfIa2GuuJoShKdyyTOnv0Kl2CvVuYscRadHj+FPI/G25sJ2yszGo+AOFzkh8J7ZgNdFom0z+odHR1WJB28gYTzmfxuINoHjnfFSTnzHFbFdRUwd4rFU+WGtRiphpHeYYIvw3YPzxQW8P9afwwmhDUUvaWZvZgSFlOccm11m6vl2EFMBo3NfG6W2ceAOIwtFHmY1Uo+DpcckIMbft9NeEFfCQNd3YJhWn/hQVa7NdDGvgRhML8LDXaVgkhLHdNtxf6LXvanEHW7gR5m+0URrap0Qv+AbIx30rGBmPZ0qJptRsUPNRZgE0WclmKgdxhzKNW9pr6k3OvJSaSrbNyvGDyAe2jFZq5dcMPir/FUoxcAuSBraveyR9YiH6ymhUwOsESDZYBnPg3aIsNWSggfgmPsNV7Xewj5/UoG3qUt0B3WN8X5XkUqAmRL4ySgfeoIWaoPKB77VnFLotH9+Zaq8JM139TqGbQAv5no2xOPf9EtW6PqyJ0BsDDX2/vRgQpiW14LLB/MB4o2DTrUpKR4bUW84hNVv5JcmyqGW371iM6WUXYL9PDTEsEUUsM+bwpCnTuoXbrTOtsae0xHdHiOvukg1yMv/WPjc+gRZLqOyNnDJqr3KBnOdoKlP1VkNM3g74aK6qoqZyiFeuMwr9O3z3dPrpmrzgZIoaERSvKGTtV5MXdZvT3/1TITzSUek1Iak+lbCWE5eg0g5cqQt7uJwl2MktFf3cfANpoELQ0vTbHDBpk9e2E8S6eyBXb0xTv4WNbA3JRetTtvlD8IoVIGdOhactB13W92UMqH8gF5Z/R2QKUvp2Y/pIQq6lWeTSh3OScL5p4gbtZvbtUPZnUWSXj+/jZnl/I42+lFjnf2f7FIf5bcYSr0WNYWViw/5MHsqvDCKzgvrG8EUcjIo/iHeKT80nPEUzLrCmtDWBX/52w3lTr6d7+VC3aS6b8EvGOLezPdAvU5pwojKPNTDOhUYE8oZzl0xdaM8FXLy61njtxhS358z6HruGFjgosXwZyXn7+NE0K4fdMbelUBwvdCnFVfnjpjLleHlKrIBHpeHD7+8gB6UZ6osHJ5y0Eflw8/Y2TWO8lnas5vr/Cm0FkvpMCQxrIpEZkII5UtuH681Xa3t95zEMj+7GQf0FTtJ5oy7ByPV+f0NV/MBlAikBHcM3I/76H9aGJC4ifCLHyOecj+oqXaw2jymI9UGSPwyc0jSdmMwH+5uH86hZ7eZirmBu+XhZT/X+dMCYffKo0yYPGIxj/GjbyWzI3cmLGc/jTRGivuXHT5dvP6EUZBdfMByD/dINFhAv7tiwE5JHR4wD+lSfMwByGJ6biD/PkUnKjETHPQjzACPwalJk2EOh/GME/wDjvWgBpWNSWP7lx32nB/L/AApAI588RO+enynP6A07erEKshU9+386bKjNgyIko7HaQfzANAxytEuEVnQnqi5HP1oxtfhWx6Dn+ZppMCgGSJ4yfYmpUEecxOxP+zg/oaAuIzqVJKjKjoQoP+fxqHfDMN6QtGR3CBsfjUzSxgfMqs49gp/LgVEsYd8pCQOxO8fqpI/SgB2Q3yERMR6qymmqOTgMMHqjH+oxQUZeAGZT6yN/WmojBgVWNSB3UH9RQA8iViCrMwHUMBmo5HdXA2SqT6EZ/DNPZZZTjMbcZAwR+tAWSPKyK4HqGyKLgMa5iAIdWBxyHjcZ/wC+aljIbJTymHoboqR+BGaj2qSSJYAfQyc/limlP4hLz0IS4xj8CKQzGCEg9KdyPl3Z9qbkdqUggcDNeaeiKAB/Dg0ox/k00cD5TS4PQ/zp2C4ucH39xTuemPxFN5AHGR3p4YnjGKLBcTcDxn86CDnOAaHK5w3X3pAQM4wfpTWori5254P509D3ww/WmZGM8gnrSBsHgk0xMkPBPOBQBgcmkDbj9/8ABh1prjBwV6ehqkSPDgDGeCfSnJt/hdsj+6c01WAHLOB+dPVAxyOnr0q0S2Lkqc7+/pipTgZPO76YzUZ2kEZyO2eCKesciLwkpDdCpBH4itEjNsFJMg+dB7SDI/Mc1MFZMAqSDzlctUPAXc7bT0OOP8aVCAgGXx2OBVIhkoKF/llQHuCf/rYp4WXAzGHXPVYwc/iDULSKwHzsGz/GhbOPfBpi73PmBY8DuGKn+YNVcksliFAyFB6+bEWFJs7gW0nT+Bhj9KRHlHyh7gY5xwwH5inGSQvuMu4Ed48E00IlR5PuKxjb/YYn+dLmXO0NuIP8SAEfjgfzqqs8kmUTJx7HP4daeWIUb7h4sH+NDg/+O0wH/apA5VLmNWU85HX9TTvtcm3GIpCeoEoyTSLMxiAEsMynjBfbt+mVp5UpklXUEfM67SB9cGgQxTmP5HnRuOMMVH4gU5TKMIs+9f4uhP601WjZhsmR29AQCfzpXiEjZIkx/DhSp/pQA9SJVwsgRR1ALA5+hqOSSQPlHZk6HdGGX9GyKXYzsC00gAA+WQkgY+tLLsAy4jZfTIzTF5iEq4Cb1z1wWP8AJqVkVFwWT3AwvP51EFBQlYp19dkoOB9D/Sljl2DG0qPWSP8AquaAJUULFlGmMR6YkDKP50xl2ZLfaSSMZQhf5YpubWTAK2jk8nE+0j8wKcEhYDMDRoOjLMGB/CgBqySopxc3IB9X3D8qUTM/XypeOuSh/SkLQ7yU+Vs4ysrKadJMoB3yNkc8yZH60AO84Ku1ohH7vcAj+VQsyMDlI+mcodxH5c/pRI0ZVSk6L6jzF/rTHdDhmdC398Nn9QKAJEaPH7qUK46qA3H502Vtpy7SkZ5Ih3Y/HBpVkAjCLOx7gCXd+h5pjsjt8+8Af3SQfxzmgaDMMoHlzqGz1KMn+FTCM4yoPHGRLwfzNQb5G4SaUL7YP58UqxOq5CMSfWILn6HFAXJjIdoB3En3B/lTDIrNxknHPyf4U4wkgMbO5UdmVCefwFMCtITmLzMf89EwR+YpXDY//9lQSwcIbv7oethFAACLRgAAUEsDBBQACAAIAD20UzwAAAAAAAAAAAAAAAAxAAAANWNmZjJjNmRlNmU4ZDk5MzVjYWQwNWNiNWExYWViZWRcc3ByaW5nZXItbmV1LmpwZ/t/4/8DBgEvN083BkYmBgZGIGT4f5vBmYGDjY2djZWDnZ2dk5ODi0eEl4ebm0dSSJhfRFZKXk5WSkZGQUVPXUFJR1lGRsNcU8fA0MTERF7d0tbCyEbP2MQIZAgjJycnDzePBC+vhJGijKIRyeD/AQZBDgY3BiNmRiUGJkFGZkHG/0cY5IHuZGUEAwYoYGRiZmFlY+fg5OIGKtgqwMDEyMzMxMLMysrCApStBcozsAiyCikaOrIJByayKxWKGDVOXMih7LTxoGjQxQ8qxklFTZxcYuISklKqauoamlompmbmFpZWzi6ubu4enl7BIaFh4RGRUckpqWnpGZlZxSWlZeUVlVXNLa1t7R2dXZMmT5k6bfqMmbMWLV6ydNnyFStXbdq8Zeu27Tt27jp0+MjRY8dPnDx16fKVq9eu37h56+Gjx0+ePnv+4uWrj58+f/n67fuPn79A/mJkYGaEAaz+EgT6i4mFhZmFHeQvRqZykAJBFlZFQzYhx0D2xEJhJaNGDhGniQs3HuRUNg76IJpUdJFLTMXkoepHkNfAPiPOY01k+QzuMYS/bjHwMDMCI49ZkMGe4TuLqIJIl+YXhtlT5qSklC3OLb4nO+3S76jr7xMTPq29sK1I2oKj+/h21dVRtsm+s4Mn+/b9Yt/XW2676wT3iu8ijEXTRRvLbarKu9eEvpN1Wyx8RCmT79LLNunwjQfz5jVt/+jAubWWVWRLALNI8MvVfgv4Ja987fwn+ON2yP7dW2e9d7p2+3z/yWPJs3dYHnhXzxM+7+U8u4tv6nTuVWxdm+87Z+lNJdbyd6nM8wr79v7Vvv9P+eW0WesbTDvWi5Ydz/m0WPC7pJujfMf6ft2JarvaLKWzjFdtrmKqNGH8Ut72/v0/tR/vTh/ZnzLtvNMl0dYNk6WXTm3jf/pP7uvrr8Gel9eW7FW7duqcad89iauCIQnJouVMDdKu9syXuhhaq4JXcBRemp75ZQGf8qOn32/YSWbzz5FMjnD/w9nwz22fi4xpbe7HqY4/4lenGRyprDjx8vfRZ/sKdv6ofdTtz99blat53c+ws+buq4L2hdpzvn9ZwL+mRnLF3OiDs2w/y+y5NnGz/LdtPf+27o653pDy2YZxwa4VATlJD/i/uZZUmjC80jSq1VjAHhjRucq4NGtqfnlpFcPzfdo2+Q8y38g8fP9OYUv/q0v69g0n10177bZl94cvs2w6eNdMO3an/1vZo53yoifTV/6Yfdgq9czipzuz9+vM3xPoZx/E/zB21l19nwvs+h82fT77ISWqev79l8GeifqyPjkO9tO0t67TP3zstPdH9w6dhAls8zzeR9pyr+N/tfNP9nLzDusLrLe0+m9Pv9bF8GDxlfgLl59ejZKY5STxVpZVJIDdePmRUn6R+YIxp97reCVv75mnHPefoXPdqs/x2R4219zyEzIWNVj+tbv16PVR+Q+T/q6ccJp/0gXGg4GX7b5e+7vLd+eiLob8b81VUhqLGuz/3wQAUEsHCFe7Z4pnBAAA/AQAAFBLAwQUAAgACAA9tFM8AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbL1X/Y7UNhD/uzyFlUoIql7Wdr7FLqgUoaJCqbSUShWq5E0mu+YSJ02cu917nj4DL8CLdWwn+3FQOMqpfyWZGc/nb8aT+aNtXZEL6HrZqIXHfOoRUHlTSLVeeIMuz1Lv0cM78zU0a1h1gpRNVwu98AKfe4Y+yId3vpn3m+aSiMqKvJZwufBKUfXgkb7tQBT9BkCf0MWwlZUU3e7l6i3kuj8wnJJnqh3Qiu4GpOV18Vz20+fMGmwrqZ/IC1lAR6omX3hxhK7j22votMxFtfBC6ih84fFrTCQFhrtpOnnVKG3ED8pLpBDSyyvAjHBDm89soHMY8koWUigTjPUDhQi5lIXeGNk4RJ0g1xt0No6pU5c3TVcsd72Gmmz/gK5BSRr7SRQECQtplAZhGHtk51g8CvwwyyLKeMQ4ZQmq7NFl9AU5QRLHaZRQnrGEB3hoZKWhH1EaZAlN4yBlLHam4WIJWmMteyK2cMjyupPFycez/nFTHUhtI5X+UbR66CwQgpG01DtjDTPXmSB/UOsKRhrHOm0gP18126XLXOBUv9q19oh1aLX+samajnQm0AgFxufKPa2M8XQvRa0MtRKjDqN0z2cZtxL2uXJPK1VJ5VwbI2dT1IxOZmRPDAGVG/zug6/EChAPHhmU1M+nD8TN+Rgqcwd+GeoVNs4xcvY62W3pnM+uYW5+Dp2CygFLYW2HZujJhUGws2UdKSCXNX46xpgSYcr1GzrgqAWsO5gcd23nEma5J+C9Rp7PJieMDz36mmucHxiPNrGY9tbYWgvvWW9CrchrnB6VRwqhDds0UgU1YJdpCw411NDJfJ8m4RnTaG8YrZq5NNsPmsbOjGk6jGeOgkf+R/HDaWgGTLsRSPHZiBOxwxFyHLJV+KIpJtuj5crOmlrimDyLzJysxRZ70ryJVd9Ug4ZljglVz5tcaDtOnYPTdKDUyOIZlmTmbYce8cC8lXILh+b7+FA64FlvEDYK+t42nT5uL6Gw6rYUOG1aFyXOYDDa7WyfpEmLcdvW3ucNkeaKYsqzxbndmzthn168F7aosby3vU8WRJDvyPbPe9yn9z0y+6Cg5aAsIg7V8W4cw0mJT9vnkI1/KzE9KjC9YYHpjRN8nKK8qWuhCqJEjeynU8BGkzSXFxEUgXycJsGcV0Rwg4bJv2bQk/iy7Qa1XomNctZGG59P79HB/5bnk1b6fJpPO+nTiX5Zlj1og/swsKA/i5NPNdoX1uFDqL6CrWYjXO/+NTT6wc+VbFtQuIwg5EERXCaIUASkkubzKQ4fUE2nwdLI3W8ZfYCqJKw0RrRskeWTnyS+9xI2eLgYjCCKW14F3fcEh4M9d2GazzBrstRYPOTjOMRbQfXkBRgVkxeXsqp8e+bJ0OUbUkgguKC8/1uhLiwnEagi36AX0MHaGjkXCsetcxB9sHZI/f7dupJ4+ZIDDMgVmNB8J/o7aj5//04pDcZKD8ajHjagHrkEeR+2sMYseqcp/eoB/BXdaXeyHgtVHnZLu2aY23u6Qh2utej0r2ZbIQZ0Z8xPUxpwGpvFKOJxFrvRiwsYC2MaRkmSRVGcJR652t80Jwg7yQsO2PUh6MeyKlxiSomIdcMgSwEtARV8lYssEyGLSpGnQR4moghY/sbh8UzB4L9t185tqR6L/HzdNQMOlYvT2X8UkrILgg3bBMd9HvDUbIpBGvMkiOOxxXyeZrgj4paYJlmaRsfB/Q8D4lBp9qWVvrU77DNl49fLFuVlyfO4gBjSIsuCKBcFjfJVJJjAHizejJ3b3UbhqJ8FnDFEZoSLLwt5ZAuHfUGjjDHOszjgQejgeoul+6Iuvd3a3bhys+Ol0v58jX+fD/8BUEsHCFYOyhJmBQAArw4AAFBLAQIUABQACAAIAD20Uzxu/uh62EUAAItGAAAvAAAAAAAAAAAAAAAAAAAAAAA5OGU4MTVlMGEyYmNhOTlhNDE1ZmFjODNjNDdhZDMxY1xLbGlwcGUtbmV1LmpwZ1BLAQIUABQACAAIAD20UzxXu2eKZwQAAPwEAAAxAAAAAAAAAAAAAAAAADVGAAA1Y2ZmMmM2ZGU2ZThkOTkzNWNhZDA1Y2I1YTFhZWJlZFxzcHJpbmdlci1uZXUuanBnUEsBAhQAFAAIAAgAPbRTPFYOyhJmBQAArw4AAAwAAAAAAAAAAAAAAAAA+0oAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAwADAPYAAACbUAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
</div> | </div> | ||
| − | + | <br\> | |
| + | [[Bild:Laufzettel.png|50px]] Notiere eine mögliche Sprungbahn auf deinem Laufzettel! | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
|align = "left" width="450"| | |align = "left" width="450"| | ||
| − | Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktion erhält also eine neue | + | Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktion erhält also eine neue Gleichung: '''<math>f(x)=ax^2</math>'''. |
| − | Mit der Manipulation des Schiebereglers hast du a verändert. | + | Mit der Manipulation des Schiebereglers hast du den Parameter a verändert. |
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen. | Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen. | ||
| Zeile 45: | Zeile 56: | ||
<div style="border: 2px solid #00CD66; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #00CD66; background-color:#ffffff; padding:7px;"> | ||
| − | ===Aufgabe | + | ===Aufgabe 6=== |
Hast du mit a etwas experimentiert?<br\> | Hast du mit a etwas experimentiert?<br\> | ||
Dann wird es dir jetzt nicht mehr schwer fallen, diese Sätze zu vervollständigen. | Dann wird es dir jetzt nicht mehr schwer fallen, diese Sätze zu vervollständigen. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | + | Ist a = 1, so nennt man den Graphen <big>Normalparabel</big>. | |
| − | Ist a > | + | Ist a > 1, dann ist die Parabel <strong> enger </strong> (gestreckt) als die Normalparabel. |
Für 0 < a < 1 ist die Parabel <strong> weiter </strong> (gestaucht) als die Normalparabel. | Für 0 < a < 1 ist die Parabel <strong> weiter </strong> (gestaucht) als die Normalparabel. | ||
Ist a negativ, so ist die Parabel <strong> nach unten geöffnet </strong>. | Ist a negativ, so ist die Parabel <strong> nach unten geöffnet </strong>. | ||
| Zeile 64: | Zeile 75: | ||
|valign="top"| | |valign="top"| | ||
| − | <ggb_applet width="600" height="600" version="3.2" ggbBase64=" | + | <ggb_applet width="600" height="600" version="3.2" ggbBase64="UEsDBBQACAAIAJOKVDwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbLbtw2FF03X0GoQJAU9ViPmfEMMnKQZpEacJsAk3qRRQFKupJYU+SUD1vj78kX9BOaH+slKc3DcA0DLroSRV7exzn3kFy97TtObkBpJkUeJZM4IiBKWTHR5JE19ckienv+YtWAbKBQlNRSddTkUTZJIzdv2fmL71a6lbeEcm9yxeA2j2rKNUREbxTQSrcA5mie2p5xRtX2Y/EHlEbvF4KTC7GxGMUoi3NlV10yPf6euoC1FIYQze4Ak567udWpz2UFtuSsYlS4eD43NCLkllWmzaPFYhqRFljTortZnAVvpZSqWm+1gY70X0DJPErjbDKdpek0W84Ws7Msxn3bsJQlMweTLikH52SymGfxPF4ulvNpls7Rbr8UhwBwswZjEFNNaA96LKxRrDocX+ifJK92WGwkE+Y93RirPB3ZMLU2W+cec1CukHei4TDMpYhWC+V1Ift1ACcLrj9vN36LT6do3ksuFVG4YTZDg+FbhK+3cXnurGJvE3uLwYdzultPlqm38N8ifL0VZyKkNtSdjEUn8RiGaeImHKLYRSMcnBbA8ygiVjBzOf4YVl4PlSbB/lfbFdi9h72xc5n8Ry5Xp/eaanUNSgAPrSOQVyutJjeUj9T5PCooWYe/YWEAhDqyfsMEwmwFjYIx79D6AS6/Gh+2573p1emYhMtBY66lQQ1jPcbV4iRmWoncXGhXKidXqGAekYoat+yUwqEDlJHxrSFsB4qVO5ho5EJjPDtETcZm9mKXXrf3oN1zgMsPNk/qdET5pqU4M0mGJqFbUEcVe3+/yGoMPQRGDtCwY3hSnXgNdrRHmbkRLbTk1sC6RDzFpSyp8SdayG9QfxI7RRLck07dYIuDZeZGNethLzzEjd0hsfSopn0vmxabRoDWXnDmUFpUIOeeCDxNNq7I2LXVBpx7f7yO5mSDdXtd73oGGy1w4tjp8ejU7lgO6JI8avBs7tFn86p/TXLS//4qncSv/cZjLmsrfDPsiGmiJxfwHHbjA27jR7n9WNcajGNi6WmYpQ8Sn/4bqE/H9EllPwY8+hpwrwPulPyww548Afz6/wH/WFpPhd/dD4j/2fIx4T0bwc/Qm2RA8eWfVpo3X6z49rVstcFLHNynsqhScPquGJBPVPmm7/CgdHMvv0/iNx84sLK1oiGOibz/+68f8TgjNE8m5ArUt68CTfGm8bt+ZryGsK8CTdZlywCPdcDjV2m8AipSgCxo2RrwEd9ZfeKtb5m6djGorTG0IB8U3bQgJiHvB9RmsLjouNLHuTzozecraU9WfPA00niW1/tXmH8KnCBjerzpQrsZqswn96QgrhdQVouzs2S6zNIknc+XizRoc+IGd7sb4JDq08O7xz/Chofi+T9QSwcI8YycdAQEAABaCgAAUEsBAhQAFAAIAAgAk4pUPPGMnHQEBAAAWgoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAA+BAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
|} | |} | ||
| − | + | <br\> | |
| + | [[Bild:Laufzettel.png|50px]] Bewerte die Aufgaben jetzt auf deinem Laufzettel! | ||
| + | <br\> | ||
Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen. | Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen. | ||
| − | + | <br> | |
| − | <div algin="left">[[Variationen/Quadratische Funktionen2/Übungen zu a|<math>\Rightarrow</math> Nächste Seite]]</div> | + | <big><div algin="left">[[Variationen/Quadratische Funktionen2/Übungen zu a|<math>\Rightarrow</math> Nächste Seite]]</div></big> |
| + | <br> | ||
<br> | <br> | ||
<div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | <div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | ||
Aktuelle Version vom 9. März 2010, 00:58 Uhr
Quadratische Funktionen und Klippenspringen
Aufgabe 5
![]() Notiere eine mögliche Sprungbahn auf deinem Laufzettel!
Notiere eine mögliche Sprungbahn auf deinem Laufzettel!
|
Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktion erhält also eine neue Gleichung:
Aufgabe 6Hast du mit a etwas experimentiert? Ist a = 1, so nennt man den Graphen Normalparabel. Ist a > 1, dann ist die Parabel enger (gestreckt) als die Normalparabel. Für 0 < a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel. Ist a negativ, so ist die Parabel nach unten geöffnet . Hast du die Aufgabe gelöst? Präge dir die jeweilige Auswirkung von a gut ein!
|
|
![]() Bewerte die Aufgaben jetzt auf deinem Laufzettel!
Bewerte die Aufgaben jetzt auf deinem Laufzettel!
Mit deinen neugewonnenen Erkenntnissen kannst du die nächsten Aufgaben lösen.

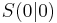 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
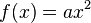 .
Mit der Manipulation des Schiebereglers hast du den Parameter a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
.
Mit der Manipulation des Schiebereglers hast du den Parameter a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
 Nächste Seite
Nächste Seite Zurück zur Übersicht
Zurück zur Übersicht
