Potenzen und Potenzfunktionen: Unterschied zwischen den Versionen
K |
|||
| (44 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Potenzen und Potenzfunktionen1}} | |
| − | + | ||
| − | {{ | + | |
| + | == Potenzen == | ||
| + | {| border="0" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left"| '''Arbeitsauftrag''' | ||
| + | -------- | ||
| + | Klick die Präsentation durch, eigentlich sollte dir alles bekannt vorkommen! Als erstes werden Potenzen betrachtet, es werden nochmal wichtige Gesetzmäßigkeiten aufgezeigt. | ||
| + | |} | ||
| + | |||
| + | |||
| + | <poem> | ||
| + | {{#slideshare:potenzen-100816043021-phpapp02}} | ||
| + | |||
| + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| + | {{pdf|Peter Fischer_Potenzen.pdf|Potenzen}} | ||
| + | |||
| + | Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Potenzen und Potenzfunktionen zusammenfasst. Du kannst es dir auch ausdrucken! | ||
| + | {{pdf|Peter Fischer_Potenzen_und_Potenzfunkionen.pdf|MindMap Potenzen und Potenzfunktionen}} | ||
| + | </poem> | ||
| + | |||
| + | ----------------------------------- | ||
| + | |||
| + | |||
| + | |||
| + | ==Aufgaben== | ||
So kannst du einige Aufgaben zu diesem Thema bearbeiten? | So kannst du einige Aufgaben zu diesem Thema bearbeiten? | ||
| − | Hier geht es darum Terme zuzuordnen. Einige sind kompliziert, andere sind mit Hilfe der Potenzgesetze vereinfacht. Finde passende Paare. | + | {| border="1" |
| − | <popup name="Tipp"> | + | ! width="12" style="background-color:#00BFFF;"| |
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
| + | Hier geht es darum Terme zuzuordnen. Einige sind kompliziert, andere sind mit Hilfe der Potenzgesetze vereinfacht. Finde passende Paare. | ||
| + | |} | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
Verwende ein Konzeptpapier und forme die Terme schrittweise um! | Verwende ein Konzeptpapier und forme die Terme schrittweise um! | ||
| − | </popup> | + | </popup> |
| + | |} | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{| | {| | ||
| Zeile 16: | Zeile 46: | ||
| <math>\frac{x^{2n-3}}{x^{n+3}}</math> || <math>x^{n}\cdot \frac{1}{x^{6}}</math> | | <math>\frac{x^{2n-3}}{x^{n+3}}</math> || <math>x^{n}\cdot \frac{1}{x^{6}}</math> | ||
|- | |- | ||
| − | | <math>\frac{x^{n}}{x^{n+1}}\cdot x^{2n}</math> || <math>x^{n-2}</math> | + | | <math>\frac{x^{n}}{x^{n+1}}\cdot x^{2n}</math> || <math>\quad x^{n-2}</math> |
|- | |- | ||
| − | | <math>\frac{(x+y)^{3+n}}{(x+y)^{1+n}}</math> || <math>x^{2}+2xy+y^{2}</math> | + | | <math>\frac{(x+y)^{3+n}}{(x+y)^{1+n}}</math> || <math>\quad x^{2}+2xy+y^{2}</math> |
|- | |- | ||
| <math>\frac{(4x^{2}+8xy+4y^{2})^{n+2}}{(4x^{2}+4y^{2})^{n+2}}</math> || <math>\left( \frac{x+y}{x-y} \right) ^{n+2}</math> | | <math>\frac{(4x^{2}+8xy+4y^{2})^{n+2}}{(4x^{2}+4y^{2})^{n+2}}</math> || <math>\left( \frac{x+y}{x-y} \right) ^{n+2}</math> | ||
| Zeile 24: | Zeile 54: | ||
| <math>\frac{\sqrt[3]{x} \cdot x^{-\frac{2}{3}}}{\sqrt[3]{x^{2}}}</math> || <math>\frac{1}{x}</math> | | <math>\frac{\sqrt[3]{x} \cdot x^{-\frac{2}{3}}}{\sqrt[3]{x^{2}}}</math> || <math>\frac{1}{x}</math> | ||
|- | |- | ||
| − | | <math>\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}</math> || <math>1</math> | + | | <math>\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}</math> || <math>\quad 1</math> |
|- | |- | ||
| − | |} | + | |}</div class="zuordnungs-quiz"> |
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 2 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
| + | Hier warten einige Gleichungen darauf gelöst zu werden, trage das Ergebnis in das entsprechende Feld ein: | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | <math>3\cdot4^{x+2}+4^{2}=64 \Leftrightarrow x=</math> { 0.00 _5} (2 Nachkommastellen) | ||
| + | <math>0,4^{2+x}-(\frac{1}{8})^{2}=63\cdot8^{-2} \Leftrightarrow x=</math> { -2 _5} | ||
| + | <math>0,5^{3-x}+2=6 \Leftrightarrow x=</math> { 5 _5} | ||
</quiz> | </quiz> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Weiter gehts zum [[/Exkurs Lineare Funktionen|Exkurs: Lineare Funktionen]]''' | |
| − | < | + | <div style="background:#00BFFF;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> |
| + | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid #00BFFF; background-color:#f6fcfe;"> | ||
| + | [[../|LERNPFAD]] | [[../Potenzen und Potenzfunktionen|Potenzen und Potenzfunktionen]] | [[../Exponential- und Logarithmusfunktion|Exponential- und Logarithmusfunktion]] | [[../Trigonometrie|Trigonometrie]] | [[../Abbildungen im Koordinatensystem|Abbildungen im Koordinatensystem]] | [[../Prüfungsaufgaben|Prüfungsaufgaben]] </div> | ||
Aktuelle Version vom 15. Oktober 2011, 12:16 Uhr
Potenzen
| Arbeitsauftrag
Klick die Präsentation durch, eigentlich sollte dir alles bekannt vorkommen! Als erstes werden Potenzen betrachtet, es werden nochmal wichtige Gesetzmäßigkeiten aufgezeigt. |
{{#slideshare:potenzen-100816043021-phpapp02}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Potenzen
Potenzen
Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Potenzen und Potenzfunktionen zusammenfasst. Du kannst es dir auch ausdrucken!
![]() MindMap Potenzen und Potenzfunktionen
MindMap Potenzen und Potenzfunktionen
Aufgaben
So kannst du einige Aufgaben zu diesem Thema bearbeiten?
| Aufgabe 1 Hier geht es darum Terme zuzuordnen. Einige sind kompliziert, andere sind mit Hilfe der Potenzgesetze vereinfacht. Finde passende Paare. |
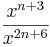 |
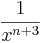
|
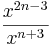 |
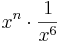
|
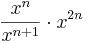 |
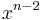
|
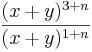 |
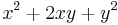
|
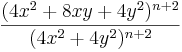 |
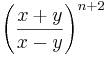
|
![\frac{\sqrt[3]{x} \cdot x^{-\frac{2}{3}}}{\sqrt[3]{x^{2}}}](/images/math/7/8/f/78ff6345ed4fbd10e7dc9a380773950d.png) |

|
![\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}](/images/math/2/3/a/23a7ce201d16e4ea02880bc7f49eaf1a.png) |
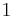
|
Leerzeile
| Aufgabe 2 Hier warten einige Gleichungen darauf gelöst zu werden, trage das Ergebnis in das entsprechende Feld ein: |
Weiter gehts zum Exkurs: Lineare Funktionen

