Potenzfunktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Struktur geändert) |
|||
| (37 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Potenzen und Potenzfunktionen}} | |
| − | {{ | + | <!-- |
| − | <ggb_applet height=" | + | ==Potenzfunktionen==--> |
| + | {| border="0" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left"| '''Arbeitsauftrag''' | ||
| + | -------- | ||
| + | Potenzfunktionen sind vielfältig. Die Präsentation versucht sie einzuordnen und dir einen Überblick zu verschaffen. Schau rein! | ||
| + | |} | ||
| + | <poem> | ||
| + | {{#slideshare:potenzfunktion-100816043034-phpapp02}} | ||
| + | |||
| + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| + | {{pdf|Peter Fischer_Potenzen.pdf|Potenzfunktionen}} | ||
| + | |||
| + | |||
| + | <ggb_applet height="550" width="750" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Potenzfunktion.ggb" /> | ||
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
| + | </poem> | ||
| − | ==Aufgabe mit einer Hyperbel | + | ==Aufgaben== |
| + | {| border="1" | ||
| + | ! width="12" style="background-color:#00BFFF;"| | ||
| + | | width="900" style="text-align:left" style="background-color:#E0FFFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]]''' | ||
| + | -------- | ||
| + | Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt. Sie ist eine frühere Prüfungsaufgabe und beschäftigt sich mit einer Hyperbel. | ||
| + | ------- | ||
Gegeben ist die Funktion f ,mit<math> y=3 \cdot x^{-1} -4 (\mathbb{G}=\mathbb{R^+}\times\mathbb{R})</math> | Gegeben ist die Funktion f ,mit<math> y=3 \cdot x^{-1} -4 (\mathbb{G}=\mathbb{R^+}\times\mathbb{R})</math> | ||
| + | |} | ||
| − | + | {| border="1" | |
| − | <popup name="Tipp"> Falls du keine Idee zur Wertemenge oder auch Definitionsmenge hast, erstelle erst die Zeichnung! | + | |Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f<sup>-1</sup> zu f. |
| + | <quiz display="simple"> | ||
| + | {Entscheide welche Gleichung die Richtige ist} | ||
| + | - <math>\quad f^{-1}: y=\frac{x+4}{3}</math> | ||
| + | + <math>\quad f^{-1}: y=\frac{3}{x+4}</math> | ||
| + | - <math>\quad f^{-1}: y=\frac{\frac{1}{3}}{x-4}</math> | ||
| + | </quiz> | ||
| + | |} | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | {| border="1" | ||
| + | |Gib die Wertemenge der Funktion an. | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> Falls du keine Idee zur Wertemenge oder auch Definitionsmenge hast, erstelle erst die Zeichnung! | ||
</popup> | </popup> | ||
| + | |} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | { | + | { |
| type="{}" } | | type="{}" } | ||
| − | <math>\mathbb{W}=\{y|y></math>{ -4 _5}} | + | '''Lösung:'''<math>\mathbb{W}=\{y|y></math>{ -4 _5}<math>\quad \}</math> |
</quiz> | </quiz> | ||
| + | |} | ||
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
| − | Für die Zeichnung: <math>1 LE = 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> | + | |
| + | {| border="1" | ||
| + | |Tabellarisiere f für <math>x \in \{0,5; 1; 2; 3; 4; 5; 6\}</math> und zeichne den Graphen in ein Koordinatensystem. | ||
| + | Für die Zeichnung: <math>\quad 1 LE \widehat{=} 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 29: | Zeile 71: | ||
|} | |} | ||
</div> | </div> | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | ||
| + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Potenzfunktion_Hyperbelast.ggb"/> | ||
| + | </popup> | ||
| + | |} | ||
| + | |} | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| − | + | |Die Punkte <math>C_n(x|3 \cdot x^{-1}-4)</math> auf dem Graphen f sind zusammen mit den Punkten <math>\quad A(-2|-2)</math> und <math>\quad B(1|-10)</math> jeweils die Eckpunkte von Dreiecken ABC<sub>n</sub>. | |
| + | Zeichne das Dreieck ABC<sub>1</sub> für <math>\quad x=1</math> und das Dreieck ABC<sub>2</sub> für <math>\quad x=4</math> in das Koordinatensystem ein. | ||
| + | |} | ||
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
| − | < | + | |
| − | + | {| border="1" | |
| − | + | |Unter den Dreiecken ABC<sub>n</sub> gibt es ein gleichschenkliges Dreieck ABC<sub>3</sub> mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C<sub>3</sub>. | |
| − | + | <quiz display="simple"> | |
| + | { | ||
| + | | type="{}" } | ||
| + | '''Lösung:'''C<sub>3</sub>({ 6.14 _5}|{ -3.51 _5}) | ||
</quiz> | </quiz> | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Lösungsschritte"> | ||
| + | '''KONSTRUKTION:''' | ||
| + | *Mittelsenkrechte über [AB] errichten, denn alle Punkte dieser Linie haben die gleiche Entfernung zu A und zu B. | ||
| + | *C<sub>3</sub> ist der Schnittpunkt der Mittelsenkrechten und dem Funktionsgraphen von f. | ||
| + | '''RECHNUNG:'''[[Bild:Peter_Fischer_Formelsammlung.png|40px]] | ||
| + | * Steigung der Geraden AB ausrechnen <math>m=\frac{y_B-y_A}{x_B-x_A}</math> | ||
| + | * Steigung der Mittelsenkrechten mit <math>m_1 \cdot m_2=-1 </math> ermittlen | ||
| + | * Mittelpunkt von [AB] berechnen <math>(M(\frac{x_B+x_A}{2}|\frac{y_B+y_A}{2}))</math> | ||
| + | * Gleichung der Mittelsenkrechten ermitteln und mit <math>\quad f(x)</math> schneiden (Gesamte Gleichung mit x durchmultiplizieren) | ||
| + | </popup> | ||
| + | |} | ||
| + | |} | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | {| border="1" | ||
| + | |Es gibt ein x für das ein Dreieck ABC<sub>4</sub> den Flächeninhalt <math>(6\sqrt{2}+5)</math> FE besitzt. Berechne dieses x. | ||
| + | [Teilergebnis: <math>A(x)=(4,5 \cdot x^{-1} +4x+5) FE</math>] | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | [[Flächenberechnung Dreieck]] | ||
| + | </popup> | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: x<sub>4</sub>={ 1.02 _5} (2 Nachkommastellen) | ||
| + | </quiz> | ||
| + | |} | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | '''Weiter gehts zu [[../Potenzfunktionsabbildungen|Potenzfunktionsabbildungen]]''' | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | <div style="background:#00BFFF;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | ||
| + | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid #00BFFF; background-color:#f6fcfe;"> | ||
| + | [[../../|LERNPFAD]] | [[../|Potenzen und Potenzfunktionen]] | [[../Exkurs Lineare Funktionen|Exkurs: Lineare Funktionen]] | [[../Exkurs Quadratische Funktionen|Exkurs: Quadratische Funktionen]] | [[../Potenzfunktionen|Potenzfunktionen]] | [[../Potenzfunktionsabbildungen|Potenzfunktionsabbildungen]] </div> | ||
| − | |||
| − | < | + | <!-- Wiki-Family-Links --> |
| − | + | [[medienvielfalt:Potenzfunktionen]] | |
| − | [[ | + | [[zum-wiki:Potenzfunktionen]] |
| + | [[zum-wiki:Mathematik-digital/Potenzfunktionen]] | ||
Aktuelle Version vom 15. Oktober 2011, 11:16 Uhr
Lernpfad-Navigator
| Arbeitsauftrag
Potenzfunktionen sind vielfältig. Die Präsentation versucht sie einzuordnen und dir einen Überblick zu verschaffen. Schau rein! |
{{#slideshare:potenzfunktion-100816043034-phpapp02}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Potenzfunktionen
Potenzfunktionen
Leerzeile
Aufgaben
| Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f-1 zu f.
|
Leerzeile
| Gib die Wertemenge der Funktion an.
|
Leerzeile
Leerzeile
Die Punkte 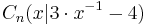 auf dem Graphen f sind zusammen mit den Punkten auf dem Graphen f sind zusammen mit den Punkten 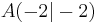 und und 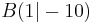 jeweils die Eckpunkte von Dreiecken ABCn. jeweils die Eckpunkte von Dreiecken ABCn.
Zeichne das Dreieck ABC1 für |
Leerzeile
| Unter den Dreiecken ABCn gibt es ein gleichschenkliges Dreieck ABC3 mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C3.
|
Leerzeile
Es gibt ein x für das ein Dreieck ABC4 den Flächeninhalt 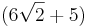 FE besitzt. Berechne dieses x. FE besitzt. Berechne dieses x.
[Teilergebnis: |
Leerzeile
Weiter gehts zu Potenzfunktionsabbildungen
Leerzeile
Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs: Lineare Funktionen | Exkurs: Quadratische Funktionen | Potenzfunktionen | Potenzfunktionsabbildungen
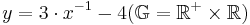
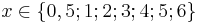 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.
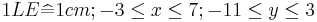
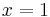 und das Dreieck ABC2 für
und das Dreieck ABC2 für 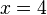 in das Koordinatensystem ein.
in das Koordinatensystem ein.
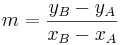
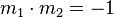 ermittlen
ermittlen
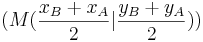
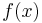 schneiden (Gesamte Gleichung mit x durchmultiplizieren)
schneiden (Gesamte Gleichung mit x durchmultiplizieren)
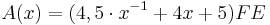 ]
]

