WR 7d:Aufgabe2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
WR7d14 (Diskussion | Beiträge) |
(Änderung 23175 von WR7d14 (Diskussion) wurde rückgängig gemacht.) |
||
| Zeile 28: | Zeile 28: | ||
---- | ---- | ||
| − | Setze ein Häckchen bei den richtigen Aussagen! | + | Setze ein Häckchen bei den richtigen Aussagen! |
<quiz display="simple"> | <quiz display="simple"> | ||
{Eine Achsenspiegelung ist } | {Eine Achsenspiegelung ist } | ||
Aktuelle Version vom 6. Juli 2010, 17:46 Uhr
- Wiederholung: Achsenspiegelung
- Doppelachsenspiegelung = Drehung
- Konstruktion
- Eigenschaften der Drehung
|
2a: Wiederholung der Achsenspiegelung Gegeben sind Gerade g, Strecke [CD] und Dreieck EFG. Wenn du an den blauen Punkten ziehst und dabei aufmerksam die Veränderungen beobachtest, kannst du dir mit Hilfe dieses Applets die Eigenschaften der Achsenspiegelung in die Erinnerung zurückrufen und die Fragen aus dem kleinen Multiple-Choice danach richtig beantworten. Viel Erfolg! |
|
|
2b: Hier kannst du dein Wissen über die Achsenspiegelung testen. Setze ein Häckchen bei den richtigen Aussagen!
|
Gut gemacht! Weiter so! Hier geht's zur Aufgabe 3
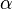 und
und 
