9 Gruppe08: Unterschied zwischen den Versionen
(→Modell erstellen) |
|||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
===<u>Aufgabe verstehen</u>=== | ===<u>Aufgabe verstehen</u>=== | ||
| − | + | Wir überlegen uns wie groß eine Turnhalle ist.<br> | |
| + | Wir überlegen uns eine größe einer Matratze. <br> | ||
| + | Danach berechnen wir die Fläche der Turnhalle. <br> | ||
| + | Abstand zwischen 2 nebeinanderliegenden Matratzen berechnen. <br> | ||
| + | Die größe der Tür.<br> | ||
| + | Senkrecht/ waagerechtliegende Matratzen berechnen.<br> | ||
| + | Die Gänge zwischen den Matratzen. <br> | ||
===<u>Modell erstellen</u>=== | ===<u>Modell erstellen</u>=== | ||
| − | + | [[Bild:Gruppe08_Joshi8.JPG|500px]] | |
| − | + | ||
===<u>Mathematik benutzen</u>=== | ===<u>Mathematik benutzen</u>=== | ||
| + | Flächeninhalt von der Turnhalle: 34 m <math>\cdot</math> 20 m = 680 m² <br> | ||
| + | Flächeninhalt einer Matratze: 2m<math>\cdot</math>90 cm = 1,80 m² <br> | ||
| + | Seite a) <br> | ||
| + | 1. Berechnung: Matratze ohne Abstand: 34m:2m = 17 <br> | ||
| + | 2. Berechnung: Matratze mit Abstand von 1 m: 34:3<math>\approx</math>11 <br> | ||
| + | Seite b)<br> | ||
| + | 1. Berechnung: Matratze ohne Abstand: 20m: 0,90m<math>\approx</math>22 Matratzen <br> | ||
| + | 2. Berechnung: Matratze mit Abstand von 1m: 20m: 1,90<math>\approx</math>10 Matratzen <br> | ||
| + | Seite c) <br> | ||
| + | 1. Berechnung ohne Abstand + Tür(1,25m): 32,75m: 2m<math>\approx</math>16 Matratzen<br> | ||
| + | 2. Berechnung mit Matratzen + Tür(1,25m): 32,75: 3m<math>\approx</math>11 Matratzen<br> | ||
| + | Seite d) <br> | ||
| + | 1. Berechnung Tür von Seitenlänge abgezogen: 20m - 2,5m = 17,5 m <br> | ||
| + | 2. Berechnung Matratze ohne Abstand: 17,5: 0,90m<math>\approx</math>19 Matratzen <br> | ||
| + | 3. Berechnung Matratze mit Abstand: 17,5: 1,90m<math>\approx</math> 9 Matratzen <br> | ||
| + | ===<u>Ergebnis erklären</u>=== | ||
| + | Es ist klar es passen 41 Matratzen in die Turnhalle von einem Flächeninhalt 680 m².<br> | ||
| + | Wir haben unsere Ergebnis gerundet (ergebnis sind die Matratzen) <br> | ||
| + | Eine Matratze hat bei uns einen Flächeninhalt von 1,90 m². <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Modellieren/Mathematisches Modellieren/Allgemeines zum Wiki| Allgemeines zum Wiki]] | [[Modellieren/Mathematisches Modellieren/Allgemeines zum Wiki| Allgemeines zum Wiki]] | ||
Aktuelle Version vom 20. Oktober 2010, 09:47 Uhr
Lösung der Hochwasseraufgabe Gruppe08
Aufgabe
Aufgabe verstehen
Wir überlegen uns wie groß eine Turnhalle ist.
Wir überlegen uns eine größe einer Matratze.
Danach berechnen wir die Fläche der Turnhalle.
Abstand zwischen 2 nebeinanderliegenden Matratzen berechnen.
Die größe der Tür.
Senkrecht/ waagerechtliegende Matratzen berechnen.
Die Gänge zwischen den Matratzen.
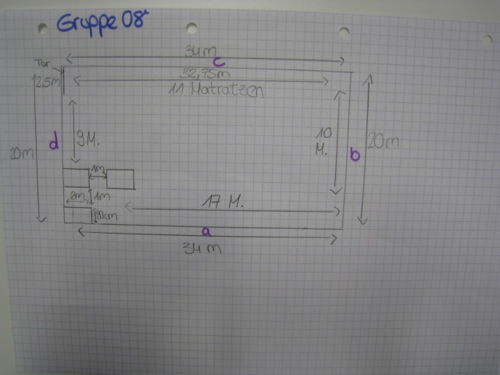
Modell erstellen
Mathematik benutzen
Flächeninhalt von der Turnhalle: 34 m 
20 m = 680 m²
Flächeninhalt einer Matratze: 2m90 cm = 1,80 m²
Seite a)
1. Berechnung: Matratze ohne Abstand: 34m:2m = 17
2. Berechnung: Matratze mit Abstand von 1 m: 34:3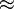
11
Seite b)
1. Berechnung: Matratze ohne Abstand: 20m: 0,90m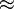22 Matratzen
2. Berechnung: Matratze mit Abstand von 1m: 20m: 1,90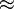10 Matratzen
Seite c)
1. Berechnung ohne Abstand + Tür(1,25m): 32,75m: 2m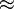16 Matratzen
2. Berechnung mit Matratzen + Tür(1,25m): 32,75: 3m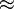11 Matratzen
Seite d)
1. Berechnung Tür von Seitenlänge abgezogen: 20m - 2,5m = 17,5 m
2. Berechnung Matratze ohne Abstand: 17,5: 0,90m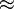19 Matratzen
3. Berechnung Matratze mit Abstand: 17,5: 1,90m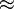 9 Matratzen
Ergebnis erklären
Es ist klar es passen 41 Matratzen in die Turnhalle von einem Flächeninhalt 680 m².
Wir haben unsere Ergebnis gerundet (ergebnis sind die Matratzen)
Eine Matratze hat bei uns einen Flächeninhalt von 1,90 m².
