Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen
(→Aufgabe 2: Ergänzungsgleiches Parallelogramme: Aufgabenstellung einfgefügt) |
(- Doppelung) |
||
| (8 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | ==Zerlegungsgleichheit von Figuren== | + | <!--==Zerlegungsgleichheit von Figuren==--> |
[[Bild:Ebert_MotivatorenEinstiegFI.jpg|center]] | [[Bild:Ebert_MotivatorenEinstiegFI.jpg|center]] | ||
| − | === | + | ===Einführung=== |
===Kapitän Check Aufgabe: Welche ist die größte Insel?=== | ===Kapitän Check Aufgabe: Welche ist die größte Insel?=== | ||
---- | ---- | ||
[[Bild:Ebert_KapitänCheckInsel.jpg|center]]<br> | [[Bild:Ebert_KapitänCheckInsel.jpg|center]]<br> | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<br> | <br> | ||
| − | <ggb_applet height= " | + | <ggb_applet height= "540" width="870" showResetIcon="true" filename="Ebert_Insel.ggb" useLocalJar = "true" /> |
<br> | <br> | ||
<br> | <br> | ||
| + | :'''''Aufgabenstellung:'''''<br> | ||
| + | : ''''' Unter den schwarzen Inseln befinden sich alle Teilfiguren, mit denen man JEDE Insel vollständig zusammensetzen kann. | ||
| + | * '''''' Beginne mit einer Insel und lege sie mit den Teilfiguren aus.''''' | ||
| + | * '''''Wenn Du Hilfe brauchst, dann Klicke die Kontrollkästchen an.''''' | ||
<br> | <br> | ||
| − | '''Trage hier den Namen der Insel ein, die am größten ist:''' | + | '''''Trage hier den Namen der Insel ein, die am größten ist:''''' |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Die größte Insel ist '''Isola Bella (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)''' | Die größte Insel ist '''Isola Bella (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)''' | ||
</div> | </div> | ||
| − | ''' | + | '''''Warum ist diese Insel die größte?''''' |
<br> | <br> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | Du siehst, auf allen drei Inseln lassen sich die gleichen Figuren legen, außer bei B. | ||
| + | Bei B brauchst Du eine Figur mehr, das kleine graue Dreieck. Also hat B den größeren Flächeninhalt und ist somit die größere Insel. | ||
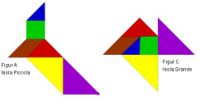
Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind. | Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind. | ||
| − | + | }} | |
<br> | <br> | ||
| Zeile 30: | Zeile 32: | ||
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid green; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | |[[Bild:Ebert_MotivatorHinweis.jpg]]|| | + | |[[Bild:Ebert_MotivatorHinweis.jpg]]|| | |
| − | * Figuren, die mit der '''gleichen Anzahl kongruenter Teilfiguren ausgelegt''' werden können, kann man natürlich auch '''in diese Teilfiguren | + | * Figuren, die mit der <span style="color: green">'''gleichen Anzahl kongruenter Teilfiguren ausgelegt'''</span> werden können, kann man natürlich auch <span style="color: green">'''in diese Teilfiguren zerlegen'''.</span> |
| + | {{versteckt|[[Bild:Ebert_Inseln.jpg|200px]] }} | ||
*Da die Inseln A und C in die gleiche Zahl kongruenter Teilfiguren zerlegt werden können, nennt man '''Figur A und C''' daher auch <span style="color:#00CD00">'''zerlegungsgleich,'''</span> | *Da die Inseln A und C in die gleiche Zahl kongruenter Teilfiguren zerlegt werden können, nennt man '''Figur A und C''' daher auch <span style="color:#00CD00">'''zerlegungsgleich,'''</span> | ||
| + | |||
| + | |||
| + | |||
|} | |} | ||
</div> | </div> | ||
| Zeile 39: | Zeile 45: | ||
---- | ---- | ||
| − | === | + | ===Das Prinzip der Zerlegungsgleichheit=== |
---- | ---- | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| [[Bild:Ebert_Zerlegungsgleiche Figuren.jpg|center]] | | [[Bild:Ebert_Zerlegungsgleiche Figuren.jpg|center]] | ||
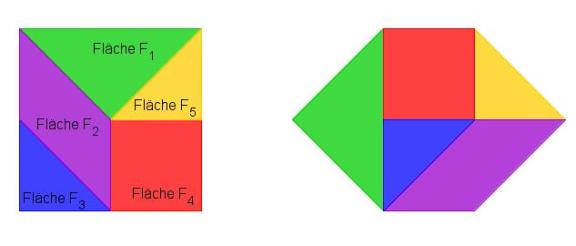
| − | + | *'''''Das Sechseck und das Quadrat wurden in jeweils <span style="color: blue">fünf Teilfiguren</span> zerlegt.'''''' | |
| − | + | *'''''Die Teilfiguren sind <span style="color: blue">paarweise zueinander kongruent</span>, denn alle Teilfiguren kommen sowohl im Quadrat, als auch im Sechseck vor''''' <br> | |
| − | + | *'''''Und da die Figuren die selben, also kongruent sind, haben sie den gleichen Flächeninhalt. | |
<br> | <br> | ||
:'''Der Flächeninhalt des Quadrates setzt sich in diesem Beispiel aus den Flächeninhalten der Teilfiguren F<sub>1</sub> bis F<sub>5</sub> zusammen.''' | :'''Der Flächeninhalt des Quadrates setzt sich in diesem Beispiel aus den Flächeninhalten der Teilfiguren F<sub>1</sub> bis F<sub>5</sub> zusammen.''' | ||
<br> | <br> | ||
| − | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | F<sub>Quadrat</sub> = | + | F<sub>Quadrat</sub> = F<sub>1</sub> + '''F<sub>2</sub>''' + F<sub>3</sub> + F<sub>4</sub> + F<sub>5</sub> = '''F<sub>Sechseck</sub>''' <br> |
Somit haben Sechseck und Quadrat in dem Beispiel den '''gleichen''' Flächeninhalt! | Somit haben Sechseck und Quadrat in dem Beispiel den '''gleichen''' Flächeninhalt! | ||
</div> | </div> | ||
| Zeile 58: | Zeile 63: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | :::'''Nils fasst hier Dein Ergebnis kurz zusammen. Übertrage es in Dein Heft:''' | + | :::'''''Nils fasst hier Dein Ergebnis kurz zusammen. Übertrage es in Dein Heft:''''' |
<br> | <br> | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | |[[Bild:Ebert_MotivatorMerke.jpg]]|| | + | |[[Bild:Ebert_MotivatorMerke.jpg|200px]]|| |
| − | * ''' | + | * '''Den Flächeninhalt einer Figur erhält man, wenn man die einzelnen Flächeninhalte der Teilfiguren addiert '''<br> |
* '''Zwei Figuren besitzen den gleichen Flächeninhalt, wenn sie in kongruente Teilfiguren zerlegt werden können''' | * '''Zwei Figuren besitzen den gleichen Flächeninhalt, wenn sie in kongruente Teilfiguren zerlegt werden können''' | ||
|} | |} | ||
</div> | </div> | ||
<br> | <br> | ||
| − | :::'''Maja | + | :::'''Maja hat noch etwas festgestellt:''' |
<br> | <br> | ||
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid green; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | |[[Bild:Ebert_MotivatorHinweis.jpg]] || | + | |[[Bild:Ebert_MotivatorHinweis.jpg|200px]] || <br> |
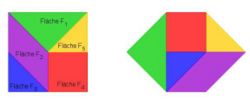
| − | * '''Man kann eine Figur also in Teilfiguren zerschneiden und diese Teilfiguren wieder | + | * '''Man kann eine Figur also in Teilfiguren zerschneiden und diese Teilfiguren wieder zu einer neuen Figur zusammensetzen.''' |
| − | [[Bild:Ebert_Zerlegungsgleiche Figuren.jpg]] <br> | + | [[Bild:Ebert_Zerlegungsgleiche Figuren.jpg|250px]] <br> |
* '''Der Flächeninhalt dieser beiden Figuren ändert sich dabei aber nicht.''' <br> | * '''Der Flächeninhalt dieser beiden Figuren ändert sich dabei aber nicht.''' <br> | ||
* <span style="color: green">'''Somit können wir feststellen, dass '''zwei Figuren den gleichen Flächeninhalt besitzen,''' <br> obwohl wir den Flächeninhalt der einzelnen Teilflächen selbst noch gar nicht berechnen können!'''</span> | * <span style="color: green">'''Somit können wir feststellen, dass '''zwei Figuren den gleichen Flächeninhalt besitzen,''' <br> obwohl wir den Flächeninhalt der einzelnen Teilflächen selbst noch gar nicht berechnen können!'''</span> | ||
| Zeile 80: | Zeile 85: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | :'''Hierzu siehst Du ein kleines Beispiel:''' | + | :'''''Hierzu siehst Du ein kleines Beispiel:''''' |
<br> | <br> | ||
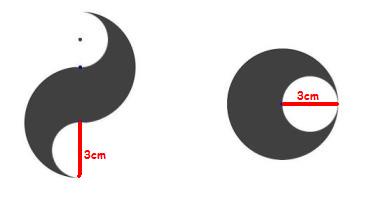
| − | :'''Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?''' | + | :'''''Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?''''' |
<br> | <br> | ||
| + | |||
[[Bild:Ebert_Halbkreisbilderneu.jpg|center]] | [[Bild:Ebert_Halbkreisbilderneu.jpg|center]] | ||
<br> | <br> | ||
'''Bist Du sicher,dass Du den Hinweis brauchst?'''<br> | '''Bist Du sicher,dass Du den Hinweis brauchst?'''<br> | ||
| − | [[Hier findest du den Hinweis ]] | + | [[/Hinweis|Hier findest du den Hinweis ]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ---- | |
| − | + | [[Bild:Ebert_Motivatoren.jpg|200px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| + | '''Hier geht es weiter zur nächsten Station:''' | ||
<br> | <br> | ||
| − | + | →[[/Zusammenfassung zur Zerlegungsgleichheit/]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 28. Dezember 2011, 14:08 Uhr
Einführung
Kapitän Check Aufgabe: Welche ist die größte Insel?
- Aufgabenstellung:
- Unter den schwarzen Inseln befinden sich alle Teilfiguren, mit denen man JEDE Insel vollständig zusammensetzen kann.
- ' Beginne mit einer Insel und lege sie mit den Teilfiguren aus.
- Wenn Du Hilfe brauchst, dann Klicke die Kontrollkästchen an.
Trage hier den Namen der Insel ein, die am größten ist:
Die größte Insel ist Isola Bella (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)
Warum ist diese Insel die größte?
Du siehst, auf allen drei Inseln lassen sich die gleichen Figuren legen, außer bei B. Bei B brauchst Du eine Figur mehr, das kleine graue Dreieck. Also hat B den größeren Flächeninhalt und ist somit die größere Insel. Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind.
Das Prinzip der Zerlegungsgleichheit
FQuadrat = F1 + F2 + F3 + F4 + F5 = FSechseck |
- Nils fasst hier Dein Ergebnis kurz zusammen. Übertrage es in Dein Heft:
- Maja hat noch etwas festgestellt:
- Hierzu siehst Du ein kleines Beispiel:
- Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?
Bist Du sicher,dass Du den Hinweis brauchst?
Hier findest du den Hinweis
Hier geht es weiter zur nächsten Station:
→Zusammenfassung zur Zerlegungsgleichheit