Zusammenfassung zur Zerlegungsgleichheit: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Link zur Unterseite geändert)
(linkfix)
 
(10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 8: Zeile 8:
 
'''Beispiel:'''  
 
'''Beispiel:'''  
 
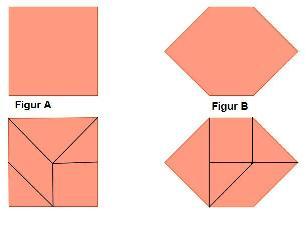
<br> [[Bild:Ebert_Merkbilder_Zerlegungsgleichheit.jpg]]
 
<br> [[Bild:Ebert_Merkbilder_Zerlegungsgleichheit.jpg]]
−
<br> Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen <span style="color:#ff0000">'''Flächeninhalt'''</span>
+
*'''Figur A und Figur B sind <span style="color: reda">zerlegungsgleich</span>. '''
 +
*'''Zerlegungsgleiche Figuren besitzen den gleichen <span style="color:#ff0000">Flächeninhalt</span>'''
 
|}
 
|}
 
</div>
 
</div>
Zeile 19: Zeile 20:
 
{|  
 
{|  
 
| [[Bild:Ebert_MotivatorHinweis.jpg]]|| '''
 
| [[Bild:Ebert_MotivatorHinweis.jpg]]|| '''
−
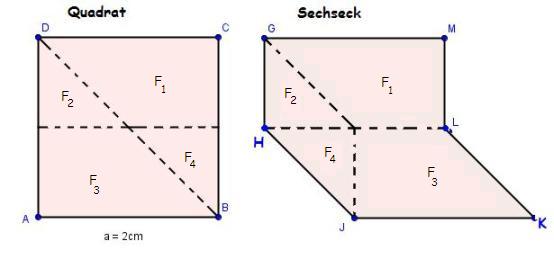
*''' Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist.'''
+
*''' Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist.'''
−
[[Bild:Ebert_Zusammenfassungsaufgabe.jpg]]  
+
[[Bild:Ebert_Zusammenfassungsaufgabeneu.jpg]]  
−
*'''Die Seitenlänge des Quadrates ist 2 cm.'''
+
*'''Die Länge der Seite a des Quadrates ist 2 cm.'''
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
−
Damit ist der Flächeninhalt '''4(cm²)'''
+
Der Flächeninhalt des Quadrates ist'''4(Zahl eintragen)cm²'''
 
</div>
 
</div>
−
* '''Da  das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks.'''  
+
* '''Da  das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks.
−
* <span style="color: #008B00">'''Man kann die Berechnung des Flächeninhaltes von Figuren, für die man keine Berechnungsformel kennt, auf Figuren zurückführen, für die man eine Flächeninhaltsformel kennt.'''</span>
+
'''  
 +
<div class="lueckentext-quiz">
 +
Damit ist der Flächeninhalt des Sechsecks'''4(Zahl eintragen)cm²'''
 +
</div>
 +
* <span style="color: #008B00">''' Figuren, von denen man keine Flächeinhaltsformel kennt, wandelt man durch Zerlegung in kongruente Teilfiguren so um, so dass man eine Figur erhält, deren Flächeninhalt wir bereits berechnen können'''</span>
 
|}
 
|}
 
</div>
 
</div>
 
<br>
 
<br>
 
<br>
 
<br>
 +
 +
----
 +
 +
===Ergänzungsgleichheit von Figuren===
 +
 +
<div style="border: 2px solid white; background-color:#ffffff; padding:7px;">
 +
{|
 +
 +
|<ggb_applet height="420" width="650"  showResetIcon="true" filename="Ebert_PrinzipErgänzungneu.ggb" /> ||
 +
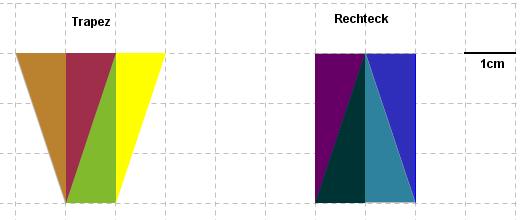
*'''''Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind'''''<br>
 +
Du brauchst doch sicher nicht den Lösungshinweis, oder?<br>
 +
{{ versteckt|
 +
[[Bild:Ebert_ZerlegungLösung.jpg]]<br>
 +
'''Dies ist eine Lösungsmöglichkeit zur Zerlegung.'''
 +
}}
 +
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
 +
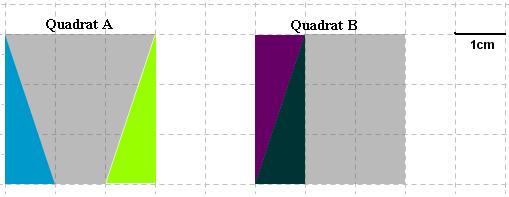
*'''''Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm:'''''<br>
 +
Vergleiche Deine Lösung hier: <br>
 +
{{ versteckt|
 +
[[Bild:Ebert_ErgänzungHinweis.jpg]]
 +
'''Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.'''
 +
}}
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
 +
*'''''Welche Eigenschaft haben die Quadrate?''''
 +
<div class="schuettel-quiz">
 +
*Die beiden Quadrate sind '''zerlegungs'''-gleich
 +
</div>
 +
 +
<br>
 +
<br>
 +
<br>
 +
|-
 +
|
 +
 +
*'''''Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren  <span style="color: green">hinzufügt</span> - also <span style="color: green">ergänzt</span>, so sind die beiden <span style="color: green">entstehenden Quadrate A und B</span> auch <span style="color: green">zerlegungsgleich</span>''''' 
 +
 +
*'''''Das Trapez und das Rechteck nennt man daher auch <span style="color: green">ergänzungsgleich</span>. '''''
 +
|}
 +
</div>
 +
 +
 +
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 +
{|
 +
|[[Bild:Ebert_MotivatorMerke.jpg|100px]]||
 +
*'''<span style="color: red">Figuren sind ergänzungsgleich</span>, wenn man sie durch <span style="color: red">Ergänzung</span> mit der <span style="color: red">gleichen Zahl kongruenter Figuren</span> in <span style="color: red">zerlegungsgleiche Figuren</span> umwandeln kann. '''
 +
*'''Ergänzungsgleiche Figuren sind zerlegungsgleich.'''
 +
|}
 +
</div>
 +
 +
 +
 +
 
'''Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:'''
 
'''Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:'''
 
<br>
 
<br>
−
[[Übung zur Zerlegungsgleichheit]]
+
→[[../Übung zur Zerlegungsgleichheit/]]
 +
 
 +
''''''Hier geht es zurück zur ''''''[[Zerlegungsgleichheit von Figuren]]

Aktuelle Version vom 28. Dezember 2011, 14:12 Uhr

Übertrage folgende Definition in Dein Heft:
Ebert MotivatorMerke.jpg

Zerlegungsgleichheit von Figuren Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können.
Beispiel:
Ebert Merkbilder Zerlegungsgleichheit.jpg

  • Figur A und Figur B sind zerlegungsgleich.
  • Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt



Anwendung der Zerlegungsgleichheit


Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:
Ebert MotivatorHinweis.jpg
  • Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist.

Ebert Zusammenfassungsaufgabeneu.jpg

  • Die Länge der Seite a des Quadrates ist 2 cm.

Der Flächeninhalt des Quadrates ist4(Zahl eintragen)cm²

  • Da das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks.

Damit ist der Flächeninhalt des Sechsecks4(Zahl eintragen)cm²

  • Figuren, von denen man keine Flächeinhaltsformel kennt, wandelt man durch Zerlegung in kongruente Teilfiguren so um, so dass man eine Figur erhält, deren Flächeninhalt wir bereits berechnen können



Ergänzungsgleichheit von Figuren
  • Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind

Du brauchst doch sicher nicht den Lösungshinweis, oder?

Ebert ZerlegungLösung.jpg
Dies ist eine Lösungsmöglichkeit zur Zerlegung.







  • Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm:

Vergleiche Deine Lösung hier:

Ebert ErgänzungHinweis.jpg Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.







  • Welche Eigenschaft haben die Quadrate?'
  • Die beiden Quadrate sind zerlegungs-gleich




  • Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren hinzufügt - also ergänzt, so sind die beiden entstehenden Quadrate A und B auch zerlegungsgleich
  • Das Trapez und das Rechteck nennt man daher auch ergänzungsgleich.


Ebert MotivatorMerke.jpg
  • Figuren sind ergänzungsgleich, wenn man sie durch Ergänzung mit der gleichen Zahl kongruenter Figuren in zerlegungsgleiche Figuren umwandeln kann.
  • Ergänzungsgleiche Figuren sind zerlegungsgleich.



Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:
→Übung zur Zerlegungsgleichheit

'Hier geht es zurück zur 'Zerlegungsgleichheit von Figuren

Von „http://dmuw.zum.de/index.php?title=Zerlegungsgleichheit_von_Figuren/Zusammenfassung_zur_Zerlegungsgleichheit&oldid=30709“