Potenzen und Potenzfunktionen: Unterschied zwischen den Versionen

Version vom 1. Juni 2010, 07:53 Uhr

Lernpfad-Navigator

	Arbeitsauftrag Klick die Präsentation durch, eigentlich sollte dir alles bekannt vorkommen! Als erstes werden Potenzen betrachtet, es werden nochmal wichtige Gesetzmäßigkeiten aufgezeigt.

So kannst du einige Aufgaben zu diesem Thema bearbeiten?

	Aufgabe 1 Hier geht es darum Terme zuzuordnen. Einige sind kompliziert, andere sind mit Hilfe der Potenzgesetze vereinfacht. Finde passende Paare.

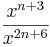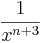
$\frac{x^{n+3}}{x^{2n+6}}$	$\frac{1}{x^{n+3}}$
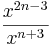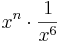
$\frac{x^{2n-3}}{x^{n+3}}$	$x^{n}\cdot \frac{1}{x^{6}}$
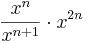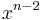
$\frac{x^{n}}{x^{n+1}}\cdot x^{2n}$	$\quad x^{n-2}$
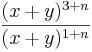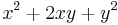
$\frac{(x+y)^{3+n}}{(x+y)^{1+n}}$	$\quad x^{2}+2xy+y^{2}$
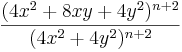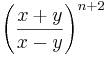
$\frac{(4x^{2}+8xy+4y^{2})^{n+2}}{(4x^{2}+4y^{2})^{n+2}}$	$\left( \frac{x+y}{x-y} \right) ^{n+2}$
$\frac{\sqrt[3]{x} \cdot x^{-\frac{2}{3}}}{\sqrt[3]{x^{2}}}$	$\frac{1}{x}$
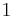
$\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}$	$\quad 1$

	Aufgabe 2 Hier warten einige Gleichungen darauf gelöst zu werden, trage das Erebnis in das entsprechende Feld ein:

Potenzen und Potenzfunktionen

@@ Zeile 57: / Zeile 57: @@
 | <math>\frac{x^{2n-3}}{x^{n+3}}</math> ||  <math>x^{n}\cdot \frac{1}{x^{6}}</math>
 |-
-| <math>\frac{x^{n}}{x^{n+1}}\cdot x^{2n}</math> ||  <math> x^{n-2}</math>
+| <math>\frac{x^{n}}{x^{n+1}}\cdot x^{2n}</math> ||  <math>\quad x^{n-2}</math>
 |-
-|  <math>\frac{(x+y)^{3+n}}{(x+y)^{1+n}}</math> ||  <math>x^{2}+2xy+y^{2}</math>
+|  <math>\frac{(x+y)^{3+n}}{(x+y)^{1+n}}</math> ||  <math>\quad x^{2}+2xy+y^{2}</math>
 |-
 | <math>\frac{(4x^{2}+8xy+4y^{2})^{n+2}}{(4x^{2}+4y^{2})^{n+2}}</math> ||  <math>\left( \frac{x+y}{x-y} \right) ^{n+2}</math>
@@ Zeile 65: / Zeile 65: @@
 |  <math>\frac{\sqrt[3]{x} \cdot x^{-\frac{2}{3}}}{\sqrt[3]{x^{2}}}</math> ||  <math>\frac{1}{x}</math>
 |-
-|  <math>\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}</math> ||  <math>1</math>
+|  <math>\frac{x^{1,5} \cdot x^{-3} \cdot \sqrt[3]{x^{4}}}{\sqrt[4]{x^{3}} \cdot x^{-\frac{11}{12}}}</math> ||  <math>\quad 1</math>
 |-
 |}</div class="zuordnungs-quiz">