Potenzfunktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 42: | Zeile 42: | ||
-------- | -------- | ||
Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt. Sie ist eine frühere Prüfungsaufgabe und beschäftigt sich mit einer Hyperbel. | Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt. Sie ist eine frühere Prüfungsaufgabe und beschäftigt sich mit einer Hyperbel. | ||
| + | ------- | ||
| + | Gegeben ist die Funktion f ,mit<math> y=3 \cdot x^{-1} -4 (\mathbb{G}=\mathbb{R^+}\times\mathbb{R})</math> | ||
|} | |} | ||
| − | + | {| border="1" | |
| − | + | |Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f<sup>-1</sup> zu f. | |
| − | + | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{Entscheide welche Gleichung die Richtige ist} | {Entscheide welche Gleichung die Richtige ist} | ||
| Zeile 53: | Zeile 54: | ||
- <math>\quad f^{-1}: y=\frac{\frac{1}{3}}{x-4}</math> | - <math>\quad f^{-1}: y=\frac{\frac{1}{3}}{x-4}</math> | ||
</quiz> | </quiz> | ||
| + | |} | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| + | |Gib die Wertemenge der Funktion an. | ||
<popup name="Tipp"> Falls du keine Idee zur Wertemenge oder auch Definitionsmenge hast, erstelle erst die Zeichnung! | <popup name="Tipp"> Falls du keine Idee zur Wertemenge oder auch Definitionsmenge hast, erstelle erst die Zeichnung! | ||
</popup> | </popup> | ||
| Zeile 64: | Zeile 67: | ||
<math>\mathbb{W}=\{y|y></math>{ -4 _5}} | <math>\mathbb{W}=\{y|y></math>{ -4 _5}} | ||
</quiz> | </quiz> | ||
| + | |} | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| + | |Tabellarisiere f für <math>x \in \{0,5; 1; 2; 3; 4; 5; 6\}</math> und zeichne den Graphen in ein Koordinatensystem. | ||
Für die Zeichnung: <math>\quad 1 LE \widehat{=} 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> | Für die Zeichnung: <math>\quad 1 LE \widehat{=} 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> | ||
| Zeile 83: | Zeile 88: | ||
</popup> | </popup> | ||
|} | |} | ||
| − | + | |} | |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| + | |Die Punkte <math>C_n(x|3 \cdot x^{-1}-4)</math> auf dem Graphen f sind zusammen mit den Punkten A(-2|-2) und B(1|-10) jeweils die Eckpunkte von Dreiecken ABC<sub>n</sub>. | ||
Zeichne das Dreieck ABC<sub>1</sub> für <math>\quad x=1</math> und das Dreieck ABC<sub>2</sub> für <math>\quad x=4</math> in das Koordinatensystem ein. | Zeichne das Dreieck ABC<sub>1</sub> für <math>\quad x=1</math> und das Dreieck ABC<sub>2</sub> für <math>\quad x=4</math> in das Koordinatensystem ein. | ||
| + | |} | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| + | |Unter den Dreiecken ABC<sub>n</sub> gibt es ein gleichschenkliges Dreieck ABC<sub>3</sub> mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C<sub>3</sub>. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ | { | ||
| Zeile 107: | Zeile 115: | ||
* Gleichung der Mittelsenkrechten ermitteln und mit <math>\quad f(x)</math> schneiden (Gesamte Gleichung mit x durchmultiplizieren) | * Gleichung der Mittelsenkrechten ermitteln und mit <math>\quad f(x)</math> schneiden (Gesamte Gleichung mit x durchmultiplizieren) | ||
</popup> | </popup> | ||
| + | |} | ||
{| | {| | ||
| Zeile 117: | Zeile 126: | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | + | {| border="1" | |
| + | |Es gibt ein x für das ein Dreieck ABC<sub>4</sub> den Flächeninhalt <math>(6\sqrt{2}+5)</math> FE besitzt. Berechne dieses x. | ||
[Teilergebnis: <math>A(x)=(4,5 \cdot x^{-1} +4x+5) FE</math>] | [Teilergebnis: <math>A(x)=(4,5 \cdot x^{-1} +4x+5) FE</math>] | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| Zeile 127: | Zeile 137: | ||
x<sub>4</sub>={ 1,02 _5} (2 Nachkommastellen) | x<sub>4</sub>={ 1,02 _5} (2 Nachkommastellen) | ||
</quiz> | </quiz> | ||
| + | |} | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
'''Weiter gehts zu [[Potenzfunktionsabbildungen]]''' | '''Weiter gehts zu [[Potenzfunktionsabbildungen]]''' | ||
Version vom 6. Juni 2010, 09:59 Uhr
Lernpfad-Navigator
Potenzfunktionen
| Arbeitsauftrag
Potenzfunktionen sind vielfältig. Die Präsentation versucht sie einzuordnen und dir einen Überblick zu verschaffen. Schau rein! |
{{#slideshare:potenzfunktion-100520132023-phpapp01}}
Leerzeile
Aufgaben
| Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f-1 zu f.
|
Leerzeile
| Gib die Wertemenge der Funktion an.
|
Leerzeile
Leerzeile
| -2) und B(1|-10) jeweils die Eckpunkte von Dreiecken ABCn.
Zeichne das Dreieck ABC1 für |
Leerzeile
| Unter den Dreiecken ABCn gibt es ein gleichschenkliges Dreieck ABC3 mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C3.
|
Leerzeile
Es gibt ein x für das ein Dreieck ABC4 den Flächeninhalt 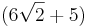 FE besitzt. Berechne dieses x. FE besitzt. Berechne dieses x.
[Teilergebnis: |
Leerzeile
Weiter gehts zu Potenzfunktionsabbildungen
Leerzeile
Potenzen und Potenzfunktionen
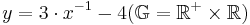
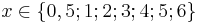 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.
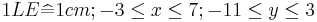
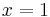 und das Dreieck ABC2 für
und das Dreieck ABC2 für 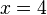 in das Koordinatensystem ein.
in das Koordinatensystem ein.
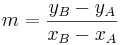
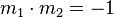 ermittlen
ermittlen
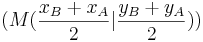
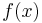 schneiden (Gesamte Gleichung mit x durchmultiplizieren)
schneiden (Gesamte Gleichung mit x durchmultiplizieren)
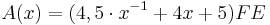 ]
]

