Formelsammlung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 32: | Zeile 32: | ||
===Einsetzen der Formelsammlung=== | ===Einsetzen der Formelsammlung=== | ||
| + | <poem> | ||
Es gibt verschiedene Gelegenheiten die Formelsammlung sinnvoll einzusetzen: | Es gibt verschiedene Gelegenheiten die Formelsammlung sinnvoll einzusetzen: | ||
[[Bild:Peter_Fischer_Lösungsformel.png|150px]]<span style="color:#00B2EE ">'''Formel gesucht!'''</span> Du weist es gibt eine Formel, aber bist nicht sicher wie sie lautet? -> Nachschlagen! | [[Bild:Peter_Fischer_Lösungsformel.png|150px]]<span style="color:#00B2EE ">'''Formel gesucht!'''</span> Du weist es gibt eine Formel, aber bist nicht sicher wie sie lautet? -> Nachschlagen! | ||
| Zeile 39: | Zeile 40: | ||
|} | |} | ||
[[Bild:Peter_Fischer_Idee.png|80px]]<span style="color:#00B2EE ">'''Gar keine Idee?'''</span> Dann kann es lohnen in der Formelsammlung zu gleichen oder ähnlichen Themen nachzusehen. | [[Bild:Peter_Fischer_Idee.png|80px]]<span style="color:#00B2EE ">'''Gar keine Idee?'''</span> Dann kann es lohnen in der Formelsammlung zu gleichen oder ähnlichen Themen nachzusehen. | ||
| − | + | </poem> | |
<div style="background:#EE2C2C;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Lernpfad</div> | <div style="background:#EE2C2C;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Lernpfad</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#0000FF; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#0000FF; background-color:#f6fcfe;"> | ||
[[LERNPFAD]] | [[Potenzen und Potenzfunktionen]] | [[Exponential- & Logarithmusfunktion]] | [[Trigonometrie]] | [[Abbildungen im Koordinatensystem]] | [[Prüfungsaufgaben]] </div><noinclude> | [[LERNPFAD]] | [[Potenzen und Potenzfunktionen]] | [[Exponential- & Logarithmusfunktion]] | [[Trigonometrie]] | [[Abbildungen im Koordinatensystem]] | [[Prüfungsaufgaben]] </div><noinclude> | ||
Version vom 21. Juni 2010, 12:36 Uhr
Inhaltsverzeichnis |
Formelsammlung
Die Formelsammlung ist ein Instrument, dass du in der Prüfung verwenden darfst, also tu dies auch!
Tipps zum Umgang mit der Formelsammlung
Es sind aktuell [Stand: 3. Mai 2010] vier Formelsammlungen für bayerische Realschulen zugelassen, deshalb werden die Erläuterungen allgemein gehalten und auch keine Seitenzahlen im Lernpfad angegeben.
Nachschlagen
Du suchst etwas und weist nicht wo es steht, hier sind drei Verfahren zu empfehlen:
- Stichwortverzeichnis: Auf den letzten Seiten steht ein Liste mit Stichwörtern, alphabetisch geornet.
- Inhaltsverzeichnis: Wenn du das Gesuchte einem Themengebiet zuordnen kannst, dann findest du dich auch schnell im Inhaltsverzeichnis zurecht.
- Die Formelsammlungen sind häufig Themengebiete farbig gekennzeichnet. So kannst du schnell zu ein Gebiet durchblättern. Besonders zu empfehlen, wenn du bereits länger mit der Formelsammlung arbeitest.
Einsetzen der Formelsammlung
Es gibt verschiedene Gelegenheiten die Formelsammlung sinnvoll einzusetzen:
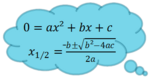Formel gesucht! Du weist es gibt eine Formel, aber bist nicht sicher wie sie lautet? -> Nachschlagen!
 |
Geometrische Figur vorgegeben? Es kommt in den Prüfungen vor, dass im Aufgabentext von Drachenvierecken, gleichseitigen Dreiecken usw. die Rede ist. Dann schlag als erstes die Formelsammlung auf, so dass du immer einen Blick auf die Eigenschaften der jeweiligen geometrischen Figur werfen kannst. |
|---|
Gar keine Idee? Dann kann es lohnen in der Formelsammlung zu gleichen oder ähnlichen Themen nachzusehen.
Lernpfad
