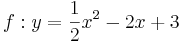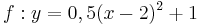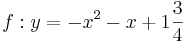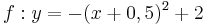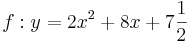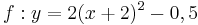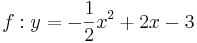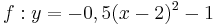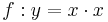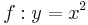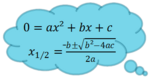Exkurs Quadratische Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 75: | Zeile 75: | ||
{ Wie kannst du die Parabel <math>y=-\frac{1}{2}x^2+3x+5</math> zeichnen? } | { Wie kannst du die Parabel <math>y=-\frac{1}{2}x^2+3x+5</math> zeichnen? } | ||
+ Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen | + Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen | ||
| − | - Den Punkt S(-3/5) einzeichnen und von dort aus die Werte der Parabel <math>y=-\frac{1}{2}</math> abtragen | + | - Den Punkt S(-3/5) einzeichnen und von dort aus die Werte der Parabel <math>y=-\frac{1}{2}x^2</math> abtragen |
- Drei Werte ausrechnen, einzeichnen und verbinden | - Drei Werte ausrechnen, einzeichnen und verbinden | ||
| − | + Den Scheitel ermitteln (Quadratische Ergänzung!), einzeichnen und von diesem aus die Werte der Parabel <math>y=-\frac{1}{2}</math> abtragen | + | + Den Scheitel ermitteln (Quadratische Ergänzung!), einzeichnen und von diesem aus die Werte der Parabel <math>y=-\frac{1}{2}x^2</math> abtragen |
- Die Parabelschablone im Koordinatenursprung nach unten ansetzen und um den Vektor <math>{-3 \choose 5}</math> verschieben | - Die Parabelschablone im Koordinatenursprung nach unten ansetzen und um den Vektor <math>{-3 \choose 5}</math> verschieben | ||
</quiz> | </quiz> | ||
| Zeile 93: | Zeile 93: | ||
| type="{}" } | | type="{}" } | ||
Brechne die Schnittpunkte der ... | Brechne die Schnittpunkte der ... | ||
| − | + | Parabeln <math>y=-\frac{1}{2}x^2+3x+5</math> und <math>\quad y=2x^2+3</math>. S({ 1 _5}/{ 5 _5}); T({ -1.80 _5}/{ 9.48 _5}) (2 Nachkommastellen) | |
</quiz> | </quiz> | ||
{| | {| | ||
Version vom 20. August 2010, 12:05 Uhr
Lernpfad-Navigator
Quadratische Funktionen
| Arbeitsauftrag
Quadratische Funktionen oder Parabeln hast du in der neunten Klasse kennengelernt. Alle Infos zu Scheitelpunkts- und Normform sind auf den folgenden Folien nochmal zusammengefast - schaus dir an! |
{{#slideshare:quadratisch-100816043041-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Quadratische Funktionen
Quadratische Funktionen
Leerzeile
Aufgaben
Nun wieder praktisches Arbeiten mit Quadratischen Funktionen.
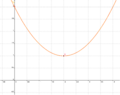
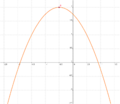
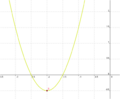
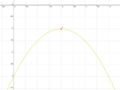
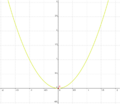
| Aufgabe 1 Ordne den Funktionsgleichungen ihre Graphen zu. Achte auf die Merkmale von Parabeln. |
Leerzeile
| Aufgabe 2
Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. |
Leerzeile
| Aufgabe 3 Berechnungen zu quadratischen Funktionen |
Leerzeile
Leerzeile
Weiter gehts zu Potenzfunktionen
Potenzen und Potenzfunktionen