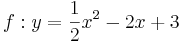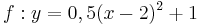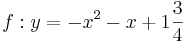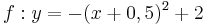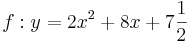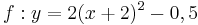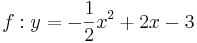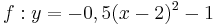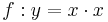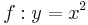Exkurs Quadratische Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 44: | Zeile 44: | ||
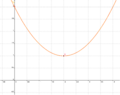
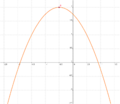
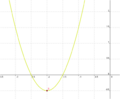
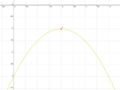
<big>'''Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu'''</big><br> | <big>'''Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu'''</big><br> | ||
{| | {| | ||
| − | | <math>y=\frac{1}{2}x^2-2x+3</math> || [[Bild:Peter Fischer_P1.png|120px]] || <math>y=0,5(x-2)^2+1</math> | + | | <math>\quad f: y=\frac{1}{2}x^2-2x+3</math> || [[Bild:Peter Fischer_P1.png|120px]] || <math>\quad f: y=0,5(x-2)^2+1</math> |
|- | |- | ||
| − | | <math>y=-x^2-x+1\frac{3}{4}</math> || [[Bild:Peter Fischer_P2.png|120px]] || <math>y=-(x+0,5)^2+2</math> | + | | <math>\quad f: y=-x^2-x+1\frac{3}{4}</math> || [[Bild:Peter Fischer_P2.png|120px]] || <math>\quad f: y=-(x+0,5)^2+2</math> |
|- | |- | ||
| − | | <math>y=2x^2+8x+7\frac{1}{2}</math> ||[[Bild:Peter Fischer_P3.png|120px]] || <math>y=2(x+2)^2-0,5</math> | + | | <math>\quad f: y=2x^2+8x+7\frac{1}{2}</math> ||[[Bild:Peter Fischer_P3.png|120px]] || <math>\quad f: y=2(x+2)^2-0,5</math> |
|- | |- | ||
| − | | <math>y=-\frac{1}{2}x^2+2x-3</math> || [[Bild:Peter Fischer_P4.png|120px]] || <math>y=-0,5(x-2)^2-1</math> | + | | <math>\quad f: y=-\frac{1}{2}x^2+2x-3</math> || [[Bild:Peter Fischer_P4.png|120px]] || <math>\quad f: y=-0,5(x-2)^2-1</math> |
|- | |- | ||
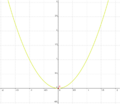
| − | | <math>y=x \cdot x</math> || [[Bild:Peter Fischer_P5.png|120px]] || <math>y=x^2 </math> | + | | <math>\quad f: y=x \cdot x</math> || [[Bild:Peter Fischer_P5.png|120px]] || <math>\quad f: y=x^2 </math> |
|} | |} | ||
</div> | </div> | ||
| Zeile 62: | Zeile 62: | ||
Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. | Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. | ||
|} | |} | ||
| − | <quiz> | + | <quiz display="simple"> |
{ Wie kannst du die Parabel <math>y=-\frac{1}{2}x^2+3x+5</math> zeichnen? } | { Wie kannst du die Parabel <math>y=-\frac{1}{2}x^2+3x+5</math> zeichnen? } | ||
+ Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen | + Wertetabelle vom Taschenrechner ausgeben lassen, Werte einzeichnen | ||
Version vom 1. Juni 2010, 07:41 Uhr
Quadratische Funktionen
| Arbeitsauftrag
Quadratische Funktionen oder Parabeln hast du in der neunten Klasse kennengelernt. Alle Infos zu Scheitelpunkts- und Normform sind auf den folgenden Folien nochmal zusammengefast - schaus dir an! |
{{#slideshare:quadratisch-100520104946-phpapp02}}
Aufgaben
Nun wieder praktisches Arbeiten mit Quadratischen Funktionen.
Aufgabe 1 
Ordne den Funktionsgleichungen ihre Graphen zu. Achte auf die Merkmale von Parabeln. |
Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
| Aufgabe 2
Entscheide mit welchen Methoden du die Parabel wirklich zeichnen kannst. |
| Aufgabe 3
Berechnungen zu quadratischen Funktionen |
Weiter gehts zu Potenzfunktionen
Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktionsabbildungen
