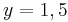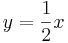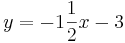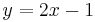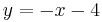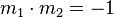Exkurs Lineare Funktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 32: Zeile 32:
  
 
<poem>
 
<poem>
−
<ggb_applet height="600" width="800" showMenuBar="true" showResetIcon="true" filename="Geraden.ggb" />
+
<ggb_applet height="600" width="800" showMenuBar="false" showResetIcon="true" filename="Geraden.ggb" />
  
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
 
<span style="color:#FFFFFF"><big>Leerzeile</big></span>

Version vom 12. Juni 2010, 14:19 Uhr

Vista-Community Help.png
Lernpfad-Navigator

LERNPFAD

Lineare Funktionen

Arbeitsauftrag

Geraden kennst du bereits aus der achten Klasse, hier sind nochmal die wichtigsten Eigenschaften zusammengefasst. Klick dich einfach durch!


{{#slideshare:linear-100609152158-phpapp02}}



Leerzeile

Aufgaben

Auch zu linearen Funktionen solltest du nun ein paar Aufgaben erledigen.


Aufgabe 1

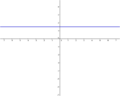
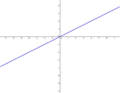
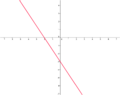
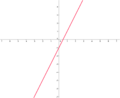
Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's!

\quad y=1,5 Peter Fischer Y=1,5.png
y=\frac{1}{2}x Peter Fischer Y=0,5x.png
y=-1\frac{1}{2}x-3 Peter Fischer Y=-1,5x-3.png
\quad y=2x-1 Peter Fischer Y=2x-1.png
\quad y=-x-4 Peter Fischer Y=-x-4.png

Leerzeile

Aufgabe 2

Sortiere die Funktionsgleichungen nach ihren Eigenschaften in Kategorien.

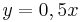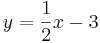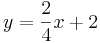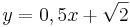
Parallele Geraden \quad y=0,5x y=\frac{1}{2}x-3 y=\frac{2}{4}x+2 y=0,5x +\sqrt{2}
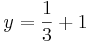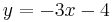
Senkrechte Geraden y=\frac{1}{3}+1 \quad y=-3x-4
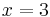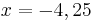
Parallele zur y-Achse \quad x=3 \quad x=-4,25
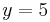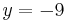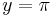
Parallele zur x-Achse \quad y=5 \quad y=-9 \quad y=\pi

Leerzeile

Aufgabe 3 Peter Fischer Papier.png

Berechnungen zu linearen Funktionen.

1.

Berechne den Schnittpunkt der Geraden
y=\frac{1}{2}x+4 und y=-x-5 \quad. S(/)
y=\frac{5}{6}x+11\frac{1}{2} und y=\frac{2}{3}x+10. \quad S(/)
Brechne die Funktionsgleichung der Geraden durch die Punkte A(2/3); \quad B(1/-2); \quad y={ x+1 _5}

Punkte: 0 / 0


Weiter gehts zu Exkurs Quadratische Funktionen

Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktionsabbildungen
Von „http://dmuw.zum.de/index.php?title=Exkurs_Lineare_Funktionen&oldid=19951“