Potenzfunktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(- Doppelung) |
|||
| Zeile 135: | Zeile 135: | ||
<div style="background:#00BFFF;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | <div style="background:#00BFFF;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid #00BFFF; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid #00BFFF; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Potenzen und Potenzfunktionen]] | [[Exkurs: Lineare Funktionen]] | [[Exkurs: Quadratische Funktionen]] | [[Potenzfunktionen]] | [[Potenzfunktionsabbildungen]] </div><noinclude> | + | [[Benutzer:Peter_Fischer|LERNPFAD]] | [[Potenzen und Potenzfunktionen]] | [[Exkurs: Lineare Funktionen]] | [[Exkurs: Quadratische Funktionen]] | [[Potenzfunktionen]] | [[Potenzfunktionsabbildungen]] </div><noinclude> |
Version vom 3. Mai 2011, 10:20 Uhr
Lernpfad-Navigator
| Arbeitsauftrag
Potenzfunktionen sind vielfältig. Die Präsentation versucht sie einzuordnen und dir einen Überblick zu verschaffen. Schau rein! |
{{#slideshare:potenzfunktion-100816043034-phpapp02}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Potenzfunktionen
Potenzfunktionen
Leerzeile
Aufgaben
| Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f-1 zu f.
|
Leerzeile
| Gib die Wertemenge der Funktion an.
|
Leerzeile
Leerzeile
Die Punkte 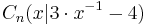 auf dem Graphen f sind zusammen mit den Punkten auf dem Graphen f sind zusammen mit den Punkten 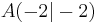 und und 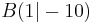 jeweils die Eckpunkte von Dreiecken ABCn. jeweils die Eckpunkte von Dreiecken ABCn.
Zeichne das Dreieck ABC1 für |
Leerzeile
| Unter den Dreiecken ABCn gibt es ein gleichschenkliges Dreieck ABC3 mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C3.
|
Leerzeile
Es gibt ein x für das ein Dreieck ABC4 den Flächeninhalt 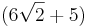 FE besitzt. Berechne dieses x. FE besitzt. Berechne dieses x.
[Teilergebnis: |
Leerzeile
Weiter gehts zu Potenzfunktionsabbildungen
Leerzeile
Potenzen und Potenzfunktionen
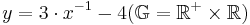
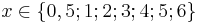 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.
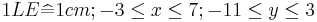
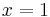 und das Dreieck ABC2 für
und das Dreieck ABC2 für 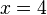 in das Koordinatensystem ein.
in das Koordinatensystem ein.
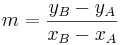
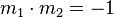 ermittlen
ermittlen
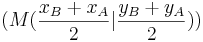
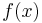 schneiden (Gesamte Gleichung mit x durchmultiplizieren)
schneiden (Gesamte Gleichung mit x durchmultiplizieren)
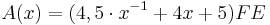 ]
]

