Eigenschaften der Achsenspiegelung: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
===Teil 2: Eigenschaften der Achsenspiegelung=== | ===Teil 2: Eigenschaften der Achsenspiegelung=== | ||
}} | }} | ||
| + | <br> | ||
| + | [[Bild:Spiegel7.jpg|400px|center]] | ||
| + | <br> | ||
| + | '''Im Teil 1 des Lernpfads hast du ja schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im 2. Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.''' | ||
| + | <br> | ||
| + | =1.Station: Besondere Punkte und Geraden= | ||
| + | <br> | ||
| + | <div style="border: 2px solid #00c5cd; background-color:#ffffff; padding:7px;"> | ||
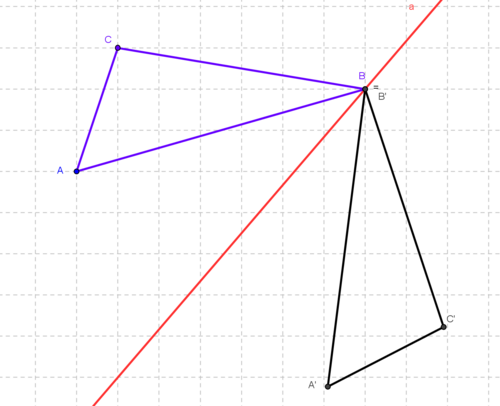
| + | Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'. | ||
| + | [[Bild:Fixpunkt.png|500px|center]] | ||
| + | <div class="schuettel-quiz"> | ||
| + | |||
| + | Finde die unverdrehte Lösung zu den verdrehten Wörtern! | ||
| + | |||
| + | Liegt ein Punkt bei einer Achsenspiegelung genau auf der Spiegelachse, nennt man einen solchen Punkt '''Fixpunkt'''. Dabei wird jeder Fixpunkt auf sich selbst '''abgebildet'''. Alle Punkte auf der '''Spiegelachse''' sind Fixpunkte. Daher ist die Spiegelachse eine '''Fixpunktgerade'''. | ||
| + | </div> | ||
| + | <br> | ||
| + | Das war ganz schön schwierig, oder? Wenn du nicht alle Wörter herausgefunden hast, sieh dir den Merksatz an! | ||
| + | </div> | ||
| + | <br> | ||
| + | Hier findest du den Merksatz! {{versteckt| | ||
| + | |||
| + | {{Merke|'''Fixpunkt und Fixpunktgerade''' <br> | ||
| + | * Ein Punkt der sich genau auf der Spiegelachse befindet, heißt '''Fixpunkt'''. [[Bild:Spiegel2.jpg|300px|right]] | ||
| + | * Jeder Fixpunkt wird auf sich selbst abgebildet, somit sind in diesem Fall Urpunkt und Bildpunkt gleich. | ||
| + | * Die Spiegelachse besteht ausschließlich aus Fixpunkten. | ||
| + | * Daher nennt man die Spiegelachse auch '''Fixpunktgerade'''. | ||
| + | <br>}} | ||
| + | }} | ||
| + | |||
<div align="left">[[Benutzer:Laura Klaus/Zulassungsarbeit über Lernpfade/Grundlagen der Achsenspiegelung|<math>\Leftarrow</math> Zurück]]</div> | <div align="left">[[Benutzer:Laura Klaus/Zulassungsarbeit über Lernpfade/Grundlagen der Achsenspiegelung|<math>\Leftarrow</math> Zurück]]</div> | ||
<br> | <br> | ||
<div align="left">[[Benutzer:Laura Klaus/Zulassungsarbeit über Lernpfade/Achsensymmetrische Vierecke und Dreiecke|<math>\Rightarrow</math> Weiter]]</div> | <div align="left">[[Benutzer:Laura Klaus/Zulassungsarbeit über Lernpfade/Achsensymmetrische Vierecke und Dreiecke|<math>\Rightarrow</math> Weiter]]</div> | ||
Version vom 6. September 2009, 18:49 Uhr
|
Lernpfad
|
Im Teil 1 des Lernpfads hast du ja schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im 2. Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.
1.Station: Besondere Punkte und Geraden
Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'.
Finde die unverdrehte Lösung zu den verdrehten Wörtern!
Liegt ein Punkt bei einer Achsenspiegelung genau auf der Spiegelachse, nennt man einen solchen Punkt Fixpunkt. Dabei wird jeder Fixpunkt auf sich selbst abgebildet. Alle Punkte auf der Spiegelachse sind Fixpunkte. Daher ist die Spiegelachse eine Fixpunktgerade.
Das war ganz schön schwierig, oder? Wenn du nicht alle Wörter herausgefunden hast, sieh dir den Merksatz an!
Hier findest du den Merksatz!
30px Merke
Fixpunkt und Fixpunktgerade
|


 Zurück
Zurück Weiter
Weiter
