Zerlegungsgleichheit von Figuren

Zerlegungsgleichheit von Figuren

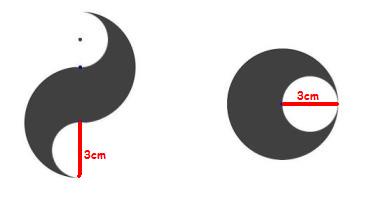
Kapitän Check Aufgabe: Welche ist die größte Insel?

---

Aufgabenstellung:

Du siehst hier die 3 schwarzen Inseln. Darunter befinden sich alle Teilfiguren, mit denen man die Inseln vollständig zusammensetzen kann. Du kannst diese Teilfiguren auf die Inseln ziehen.

• Überlege Dir zunächst selbst, wo die nächste Teilfigur platziert werden könnte.
• Wenn Du eine Hilfestellung brauchst, dann Klicke die Kontrollkästchen an.
• Was fällt Dir auf? Welche ist die größte Insel?

Trage hier den Namen der Insel ein, die am größten ist:

Die größte Insel ist (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)

Begründe Deine Antwort, warum ist diese Insel die größte?
[Lösung anzeigen][Lösung ausblenden]

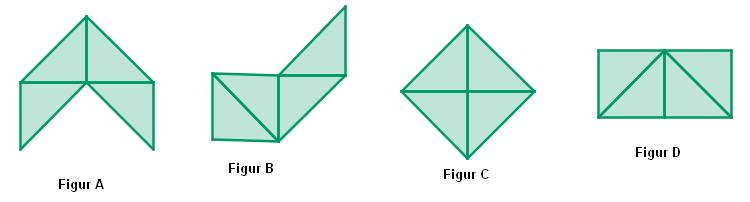
Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind.

Figur B kann mit einer Teilfigur, dem grauen Dreieck mehr ausgelegt werden, deshalb ist sie die größte der drei Inseln.

Figuren, die mit der gleichen Anzahl kongruenter Teilfiguren ausgelegt werden können, kann man natürlich auch in diese Teilfiguren zerlegen. Da die Inseln A und B in die gleiche Zahl kongruenter Teilfiguren zerlegt werden können, nennt man Figur A und C daher auch zerlegungsgleich,

---

2.Station: Das Prinzip der Zerlegungsgleichheit

---

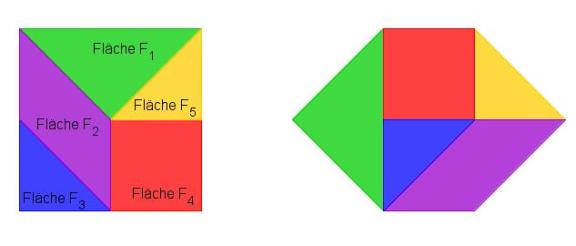
Das Sechseck und das Quadrat wurden in jeweils fünf Teilfiguren zerlegt. Diese Teilfiguren sind paarweise zueinander kongruent, d.h. es gibt immer ein Paar zueinander kongruenter Figuren. Aus den Eigenschaften der Kongruenz ergibt sich daher, dass diese Teilfiguren den gleichen Flächeninhalt besitzen. Der Flächeninhalt des Quadrates setzt sich in diesem Beispiel aus den Flächeninhalten der Teilfiguren F1 bis F5 zusammen. Ergänze die fehlenden Felder FQuadrat =                     + F2 +                     + F4 +                     =                    Somit haben Sechseck und Quadrat in dem Beispiel den                     Flächeninhalt! FSechseckF1F5F3gleichen

Nils fasst hier Dein Ergebnis kurz zusammen. Übertrage es in Dein Heft:

Der Flächeninhalt der Gesamtfigur ergibt sich aus der Addition der Flächeninhalte der Teilfiguren. Zwei Figuren besitzen den gleichen Flächeninhalt, wenn sie in kongruente Teilfiguren zerlegt werden können

Maja möchte Dir auch noch etwas sagen:

Das ist ja klasse! Man kann eine Figur also in Teilfiguren zerschneiden und diese Teilfiguren wieder zu einer neuen Figur zusammensetzen. Der Flächeninhalt dieser beiden Figuren ändert sich dabei aber nicht. Somit können wir feststellen, dass zwei Figuren den gleichen Flächeninhalt besitzen, obwohl wir den Flächeninhalt der einzelnen Teilflächen selbst noch gar nicht berechnen können!

Hierzu siehst Du ein kleines Beispiel:

Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?

Hier findest du den Hinweis

3. Station: Zusammenfassung

Übertrage folgende Definition in Dein Heft:

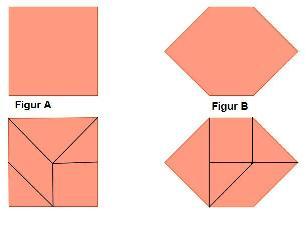
Zerlegungsgleichheit von Figuren Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können. Beispiel: Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt

4.Station: Anwendung

Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:

Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist. Da das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks. Man kann die Berechnung des Flächeninhaltes von Figuren, für die man keine Berechnungsformel kennt, auf Figuren zurückführen, für die man eine Flächeninhaltsformel kennt.

Aufgabe 1

Begründe, warum die folgenden Figuren A, B, C und D den gleichen Flächeninhalt besitzen:

Aufgabe 2: Ergänzungsgleiches Parallelogramme

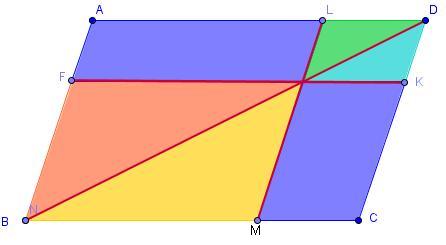
Maja zerschneidet das Parallelogramm ABCE entlang den roten Linien. [BD] ist die Diagonale, [FK] die eine Parallele zur Seite [BC] und [LM] eine Parallele zu den anderen [AB] Die Strecken schneiden sich im Punkt S

Warum besitzen die beiden blauen enstehenden Teilparallelogramme AFSL und MCKS den gleichen Flächeninhalt?

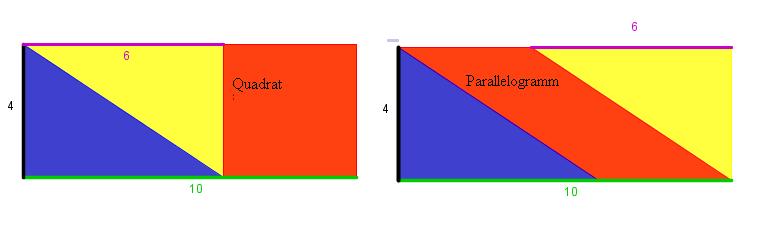
Aufgabe 3: Ergänzungsgleiche Figuren

Zeige, dass das Quadrat und das Parallelogramm den gleichen Flächeninhalt haben: