Kongruenz von Dreiecken: Unterschied zwischen den Versionen
K |
K |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation Wiederholungen zum Dreieck}} | ||
| + | |||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Zeile 23: | Zeile 26: | ||
<ggb_applet height="550" width="800" showResetIcon="true" filename="KS Kongruenz2.ggb" /> | <ggb_applet height="550" width="800" showResetIcon="true" filename="KS Kongruenz2.ggb" /> | ||
| − | <br /><br /> | + | <br /> |
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | [[Bild:Dreieck.png]] || Es war ganz schön umständlich in der letzten Aufgabe das rote Dreieck auf das orangefarbene abzubilden, indem man die Symmetrieachse und den Drehpunkt verschiebt, findest du nicht? <br /> | ||
| + | Es geht auch einfacher die Kongruenz von zwei Dreiecken nachzuweisen: Um ein Dreieck eindeutig festzulegen braucht man eine bestimmte Anzahl von Bestimmungsstücken. | ||
| + | |} | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | Was denkst du, wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? | ||
| + | (3) (!2) (!4) (!1) (!5) (!6) | ||
| + | </div> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <div class="schuettel-quiz"> | ||
| + | Um ein '''Dreieck''' eindeutig festlegen zu können benötigt man also '''drei''' Bestimmungsstücke! </div> | ||
| + | || [[Bild:Dreieck.png]] | ||
| + | |} | ||
| + | |||
| + | <br /> | ||
| + | Wir haben am Anfang des Lernpfades schon gesehen, dass ein Dreieck aus verschiedenen Teilen besteht, nämlich aus den Seiten und den Winkeln. | ||
| + | {{versteckt|[[Bild:Merke1.png]]}} <br /> | ||
| + | <u>Das heißt also, dass man ein Dreieck festlegen kann wenn man folgende Bestimmungsstücke gegeben hat:</u> | ||
| + | <br />- alle drei Seitenlängen ''oder'' | ||
| + | <br />- 2 Seitenlängen und 1 Winkel ''oder'' | ||
| + | <br />- 1 Seitenlänge und 2 Winkel | ||
| + | |||
| + | <br /> | ||
[[Bild:Dreieck.png]]<div algin="left">[[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck/Zusatzaufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben machen.]]</div> | [[Bild:Dreieck.png]]<div algin="left">[[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck/Zusatzaufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben machen.]]</div> | ||
<br /> | <br /> | ||
| − | Ansonsten geht es hier weiter | + | Ansonsten geht es hier weiter zu einem der beiden nächsten Lernpfade, wo wir die vier Kongruenzsätze kennen lernen werden: <br /> |
| + | * [[Benutzer:Kathrin_Fuchs/SSS_und_SWS | SSS-Satz und SWS-Satz]]<br /> | ||
| + | * [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g | WSW-Satz und SSW<sub>g</sub>-Satz]] | ||
Aktuelle Version vom 22. Februar 2010, 11:28 Uhr
 |
Du hast in den vergangenen Jahren im Mathematikunterricht gelernt was eine Achsenspiegelung, Drehung oder Parallelverschiebung ist.
Zur Erinnerung:
Beachte: Eine Achsenspiegelung ändert den Umlaufsinn. |
Hier eine kleine Erinnerung zur Achsenspiegelung:
du kannst das Dreieck spiegeln und die Punkte A, B und C veschieben
Hier eine kleine Erinnerung zur Drehung:
du kannst die Punkte A, B, C und D verschieben und das Dreieck mit Hilfe des Schiebereglers um den Punkt D drehen.
Wie wäre es mit einer Aufgabe?
Versuche das rote Dreieck durch Achsenspiegelung und Drehung auf das orangefarbene Dreieck abzubilden!
Das war nicht so schwer.
Versuche hier wieder das rote Dreieck auf das orangefarbene Dreieck abzubilden.
Hier musst du zusätzlich die Symmetrieachse an den Punkten S1 und S2 und den Drehpunkt D verschieben.
| |
Es war ganz schön umständlich in der letzten Aufgabe das rote Dreieck auf das orangefarbene abzubilden, indem man die Symmetrieachse und den Drehpunkt verschiebt, findest du nicht? Es geht auch einfacher die Kongruenz von zwei Dreiecken nachzuweisen: Um ein Dreieck eindeutig festzulegen braucht man eine bestimmte Anzahl von Bestimmungsstücken. |
Was denkst du, wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? (3) (!2) (!4) (!1) (!5) (!6)
|
Um ein Dreieck eindeutig festlegen zu können benötigt man also drei Bestimmungsstücke!
|
|
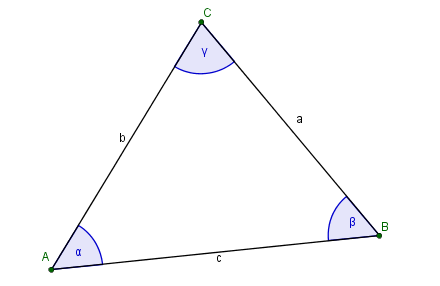
Wir haben am Anfang des Lernpfades schon gesehen, dass ein Dreieck aus verschiedenen Teilen besteht, nämlich aus den Seiten und den Winkeln.
Das heißt also, dass man ein Dreieck festlegen kann wenn man folgende Bestimmungsstücke gegeben hat:
- alle drei Seitenlängen oder
- 2 Seitenlängen und 1 Winkel oder
- 1 Seitenlänge und 2 Winkel
Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben machen.
Ansonsten geht es hier weiter zu einem der beiden nächsten Lernpfade, wo wir die vier Kongruenzsätze kennen lernen werden:
