Zusatzaufgaben: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
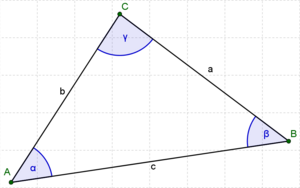
| a und c || Der Winkel β wird von den Seiten _____ eingeschlossen. | | a und c || Der Winkel β wird von den Seiten _____ eingeschlossen. | ||
|- | |- | ||
| − | | | + | | griechischen || Die Buchstaben zur Bezeichnung von Winkeln kommen aus dem _____ Alphabet. |
|- | |- | ||
| Winkel|| Im Dreieck liegt die größere Seite dem größeren _____ gegenüber. | | Winkel|| Im Dreieck liegt die größere Seite dem größeren _____ gegenüber. | ||
| Zeile 92: | Zeile 92: | ||
</div> | </div> | ||
<br /><br /> | <br /><br /> | ||
| − | Wenn du fertig bist, geht es hier weiter | + | Wenn du fertig bist, geht es hier weiter zu einem der nächsten Lernpfade, wo wir die vier Kongruenzsätze kennen lernen werden: <br /> |
| + | * [[Benutzer:Kathrin_Fuchs/SSS_und_SWS | SSS-Satz und SWS-Satz]]<br /> | ||
| + | * [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g | WSW-Satz und SSW<sub>g</sub>-Satz]] | ||
Aktuelle Version vom 26. Februar 2010, 20:15 Uhr
Lernpfad Wiederholung Dreiecke: Wiederholung 1.Teil - Wiederholung 2.Teil - Seiten-Winkel-Beziehung - Dreiecksungleichung - Kongruenz von Dreiecken - Weitere Aufgaben
 Du warst bisher also besonders schnell, super!
Du warst bisher also besonders schnell, super!
Fangen wir mit einem Kreuzworträtsel an:
Beim Klick auf die Ziffern im Kreuzworträtsel öffnet sich ein Eingabefeld zum Eintragen.
| 6 | |||||||||||||||||
| 9 | |||||||||||||||||
| 1 | |||||||||||||||||
| 2 | 7 | ||||||||||||||||
| 10 | 8 | ||||||||||||||||
| 3 | |||||||||||||||||
| 4 | |||||||||||||||||
| 5 | |||||||||||||||||
Benutzen Sie zur Eingabe die Tastatur. Eventuell müssen sie zuerst ein Eingabefeld durch Anklicken aktivieren.
- Senkrecht
- Was zeigt das Bild in der allerersten Aufgabe an? Du hast es dir auf deinem Merkzettel notiert.1
- Die Buchstaben zur Bezeichnung von Winkeln kommen aus dem _____ Alphabet.6
- Achsenspiegelung, Drehung und Parallelverschiebung nennt man auch _____.7
- Der Winkel β wird von den Seiten _____ eingeschlossen.8
- Im Dreieck liegt die größere Seite dem größeren _____ gegenüber.9
- In einem gleichschenkligen Dreieck sind zwei _____ gleich lang.10
- Waagrecht
- Die Achsenspiegelung ändert den _____ im Dreieck.2
- Ein 90° Winkel ist ein _____ Winkel.3
- Wie nennt man ein Dreieck, bei dem alle drei Winkel gleich groß sind?4
- Die Summe von zwei _____ ist stets größer als die Länge der dritten Seite.5
Ein kleines Puzzle:
Wie wäre es mit einem weiteren Memo-Quiz?
Du wirst staunen wo in deiner Umgebung überall Dreiecke vorkommen können!
Wenn du immernoch viel Zeit hast gibt es hier nochmal ein Memo-Quiz:
Wenn du fertig bist, geht es hier weiter zu einem der nächsten Lernpfade, wo wir die vier Kongruenzsätze kennen lernen werden: