Trigonometrische Funktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...)
 
Zeile 36: Zeile 36:
  
 
==Aufgaben==
 
==Aufgaben==
−
Hier warten nun Aufgaben zu Exponentialfunktionen, diese sind auch sehr häufig in der Abschlussprüfugn zu finden!
+
Es geht nun darum Sinus, Cosiunus un  Tangens als Rechenwerkzeuge kennen zu lernen!
  
 
{| border="1"
 
{| border="1"
 
! width="12" style="background-color:#FFD700;"|
 
! width="12" style="background-color:#FFD700;"|
−
| width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 '''
+
| width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Taschenrechner.png]]|40px'''
 
--------
 
--------
−
Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's! 
+
Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt.
 
|}
 
|}
 
<div class="zuordnungs-quiz">
 
<div class="zuordnungs-quiz">
 +
<big>'''Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu'''</big><br>
 
{|  
 
{|  
−
| <math>\quad f(x) = 0,5^{x-3}+2</math>|| [[Bild:Peter Fischer_F1.png|120px]]
+
| <math>\sin \alpha=\frac{1}{2}</math> || <math>\quad \alpha=30^\circ</math> ||  <math>\quad \alpha=150^\circ</math>
 
|-
 
|-
−
| <math>\quad f(x) = 0,1^{x+5}-3</math> || [[Bild:Peter Fischer_F2.png|120px]]
+
| <math>\sin \alpha=0,707 \quad</math> || <math>\quad \alpha=315^\circ</math> ||  <math>\quad \alpha=225^\circ</math>
 
|-
 
|-
−
| <math>\quad f(x) = 3 \cdot 2^x-2</math> ||[[Bild:Peter Fischer_F3.png|120px]]
+
| <math>\cos \alpha=\frac{1}{2}</math> || <math>\quad \alpha=60^\circ</math>  ||  <math>\quad \alpha=300^\circ</math>
 
|-
 
|-
−
| <math>\quad f(x) = 1,5^{x+4}-0,5</math> || [[Bild:Peter Fischer_F4.png|120px]]
+
| <math>\cos \alpha=-0,866 \quad</math> ||  <math>\quad \alpha=210^\circ</math> ||  <math>\quad \alpha=150^\circ</math>
−
|}
+
|-
 +
| <math>\tan \alpha=-0,577}</math> \quad|| <math>\quad \alpha=210^\circ</math>  ||  <math>\quad \alpha=330^\circ</math>
 +
|-
 +
| <math>\tan \alpha=1 \quad</math>||  <math>\quad \alpha=45^\circ</math>  ||  <math>\quad \alpha=135^\circ</math>
 
</div>
 
</div>
  

Version vom 6. Juni 2010, 13:57 Uhr

Vista-Community Help.png
Lernpfad-Navigator

LERNPFAD

Trigonometrische Funktionen

Arbeitsauftrag

Sinus, Cosinus und Tangens sind neben Rechenwerkzeugen auch Funktionen. Hier werden Funktionsgraphen, Definitions- und Wertemengen näher betrachtet. Schau rein!

{{#slideshare:trigonometrischefunktionen-100603045018-phpapp01}}



Leerzeile


Aufgaben

Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!

Aufgabe 1 Peter Fischer Taschenrechner.png|40px

Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt.

Ordne der Normalform die passende Scheitelform und den Funktionsgraphen zu

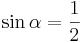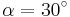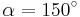
\sin \alpha=\frac{1}{2} \quad \alpha=30^\circ \quad \alpha=150^\circ
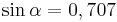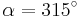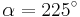
\sin \alpha=0,707 \quad \quad \alpha=315^\circ \quad \alpha=225^\circ
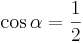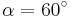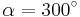
\cos \alpha=\frac{1}{2} \quad \alpha=60^\circ \quad \alpha=300^\circ
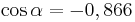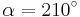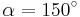
\cos \alpha=-0,866 \quad \quad \alpha=210^\circ \quad \alpha=150^\circ
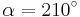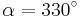
Fehler beim Parsen(Syntaxfehler): \tan \alpha=-0,577} \quad \quad \alpha=210^\circ \quad \alpha=330^\circ
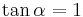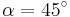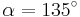
\tan \alpha=1 \quad \quad \alpha=45^\circ \quad \alpha=135^\circ

Leerzeile

Aufgabe 2 Peter Fischer Papier.png

Berechnungen zu Exponentialfunktionen.

1.

Die Gleichung f_1: y=7-7 \cdot 2,72^{-0,5x} beschreibt welche Spannung y nach x Sekunden an einem Kondensator anliegt. Die maximale Spannung (Sättigungsspannung) ist 7V. Wie viel Prozent der Sättigungsspannung hat der Kondensator nach 2,60s erreicht? (Abschlussprüfung 2004; Aufgabengruppe A; 1.2)
Lösung:%
Karl der Große (742-814) wurde im Jahr 800 römischer Kaiser. Angenommen er hätte in diesem Jahr einen Cent für dich angelegt auf einem Sparbuch. Du bekommst jährlich 2% Zins, der Zinsertrag bleibt auf dem Sparbuch. Wie viel Geld hättest du im Jahr 2010?
Lösung: Mio. € (Auf ganze Milionen gerundet)

Punkte: 0 / 0


Weiter gehts zu Trigonometrische Funktionen
Leerzeile

Potenzen und Potenzfunktionen
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Prüfungsvorbereitung/Trigonometrie/Trigonometrische_Funktionen&oldid=19659“

Navigationsmenü