Trigonometrie: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 59: Zeile 59:
 
|}
 
|}
 
</div>
 
</div>
 +
 +
<span style="color:#FFFFFF"><big>Leerzeile</big></span>
 +
 +
{| border="1"
 +
! width="12" style="background-color:#FFD700;"|
 +
| width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 2 [[Bild:Peter_Fischer_Papier.png|40px]] '''
 +
--------
 +
Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können.
 +
|}
 +
<quiz display="simple">
 +
{
 +
| type="{}" }
 +
<math>sin² \alpha +2 cos \alpha =0,5</math>
 +
<popup name="Tipp">
 +
*<math>sin² \alpha \text{durch} 1-\cos² \alpha</math> ersetzen
 +
*Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen
 +
</popup>
 +
Lösung: <math>\alpha_1</math>={ 73,14 _7}; <math>alpha_2={ 286,86 _7}</math> (2 Nachkommastellen)
 +
<math>\sin \alpha=\sqrt{3} \cdot \cos \alpha</math> { -2 _5}
 +
<popup name="Tipp">
 +
<math>\frac{\sin \alpha}{\cos \alpha}=\tan \alpha</math>
 +
</popup>
 +
Lösung: <math>\alpha_1</math>={ 60,00 _7}; <math>alpha_2={ 240,00 _7}</math>
 +
</quiz>
 +
  
  

Version vom 6. Juni 2010, 22:38 Uhr

25px
Lernpfad-Navigator

LERNPFAD

Trigonometrie

Arbeitsauftrag

Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch!

{{#slideshare:sinuskosinustangens-100603045012-phpapp02}}



Leerzeile


Aufgaben

Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!

Aufgabe 1 Peter Fischer Taschenrechner.png

Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt.

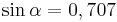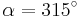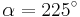
\sin \alpha=0,707 \quad \quad \alpha=315^\circ \quad \alpha=225^\circ
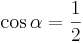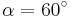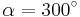
\cos \alpha=\frac{1}{2} \quad \alpha=60^\circ \quad \alpha=300^\circ
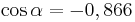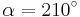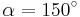
\cos \alpha=-0,866 \quad \quad \alpha=210^\circ \quad \alpha=150^\circ
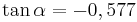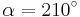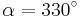
\tan \alpha=-0,577 \quad \quad \alpha=210^\circ \quad \alpha=330^\circ
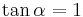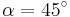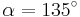
\tan \alpha=1 \quad \quad \alpha=45^\circ \quad \alpha=135^\circ

Leerzeile

Aufgabe 2 Peter Fischer Papier.png

Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können.

1.

Fehler beim Parsen(Lexikalischer Fehler): sin² \alpha +2 cos \alpha =0,5
*Fehler beim Parsen(Lexikalischer Fehler): sin² \alpha \text{durch} 1-\cos² \alpha ersetzen
*Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen
</popup>
Lösung: \alpha_1=; alpha_2={ 286,86 _7} (2 Nachkommastellen)
\sin \alpha=\sqrt{3} \cdot \cos \alpha
\frac{\sin \alpha}{\cos \alpha}=\tan \alpha
</popup>
Lösung: \alpha_1=; alpha_2={ 240,00 _7}

Punkte: 0 / 0



Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile

Potenzen und Potenzfunktionen
LERNPFAD | Trigonometrie | Trigonometrische Funktionen | Berechnungen in Dreiecken | Skalarprodukt | Exkurs: Figuren und ihre Eigenschaften
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Prüfungsvorbereitung/Trigonometrie&oldid=19664“