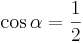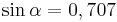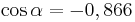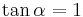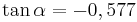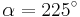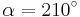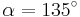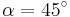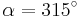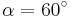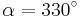Abbildung durch Achsenspiegelung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
|||
| Zeile 12: | Zeile 12: | ||
**[[Abbildung durch Achsenspiegelung]] | **[[Abbildung durch Achsenspiegelung]] | ||
**[[Weitere Abbildungen]] | **[[Weitere Abbildungen]] | ||
| + | *[[Prüfungsaufgaben]] | ||
</div> | </div> | ||
<div style="font-size:90%; padding: .5em; background-color:#D15FEE; border-top:1px solid #aaaaaa;"> | <div style="font-size:90%; padding: .5em; background-color:#D15FEE; border-top:1px solid #aaaaaa;"> | ||
Version vom 10. Juni 2010, 12:05 Uhr
Abbildungen im Koordinatensystem
| Arbeitsauftrag
Die Achsenspiegelung ist eine grundlegende Abbildung, die du seit der sechsten Klasse kennt. Jetzt kannst auch Achsenspiegelungen an Ursprungsgeraden berechnen:|} {{#slideshare:achsenspiegelung-100609155221-phpapp02}}
AufgabenEs geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!
Leerzeile
Leerzeile
Abbildungen im Koordinatensystem
|