Weitere Abbildungen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
|||
| Zeile 36: | Zeile 36: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | Es | + | Es folgen nun Teilaufgaben aus ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigen. |
{| border="1" | {| border="1" | ||
| − | ! width="12" style="background-color:# | + | ! width="12" style="background-color:#FFD700;"| |
| − | | width="1000" style="text-align:left" style="background-color:# | + | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | + | Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; A2 (verändert)). | |
| + | ------------ | ||
| + | Die gleichschenkligen Dreiecke <math>AB_nC_n \quad</math> bilden eine Dreiecksschar mit dem gemeinsamen Punkt <math>\quad A(0|0)</math>. Auf der Geraden g mit der Gleichugn <math>\quad y=-2x+6</math> liegen die Mittelpunkte <math>\quad M_n(x|-2x+6)</math> der Hyptenusen <math>\quad[AB_n]</math>. | ||
|} | |} | ||
| − | |||
| − | {| | + | {| |
| − | | | + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] |
| − | | | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Gleichschenklig-Rechtwinklig.ggb"/> |
| − | + | </popup> | |
| − | + | |} | |
| − | + | ||
| − | + | {| border="1" | |
| − | + | |Stellen Sie die Koordinaten der Punkte <math>\quad C_n</math> in Abhängigkeit der Abzisse x der Punkte <math>\quad M_n</math> dar. | |
| − | + | <popup name="Lösungshinweis"> <math>\vec{AM_n} -> \vec{AM_^*} -> \vec{AC_n}</math> und AC<sub>2</sub> Zunächst eine Drehung um <math>45^circ</math> und dann eine zentrische Streckung um <math>k=\sqrt{2}</math>.</popup> | |
| − | | | + | <quiz display="simple"> |
| − | + | { | |
| + | | type="{}" } | ||
| + | Lösung: <math>\quad C_n</math>=({ 3x-6 _7}|{ -x+6 _7}) | ||
| + | </quiz> | ||
|} | |} | ||
</div> | </div> | ||
Version vom 10. Juni 2010, 11:40 Uhr
Lernpfad-Navigator
Weitere Abbildungen
| Arbeitsauftrag
Es gibt noch weitere Abbildungen, die du bereits berechnen kannst,wie Orthogonale Affinität und Zentrische Strekung. Auch deren Abbildagleichungen sind noch einmal dargestellt. |
{{#slideshare:weitereabbildungen-100609155242-phpapp01}}
Leerzeile
Aufgaben
Es folgen nun Teilaufgaben aus ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigen.
Stellen Sie die Koordinaten der Punkte 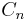 in Abhängigkeit der Abzisse x der Punkte in Abhängigkeit der Abzisse x der Punkte 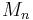 dar. dar.
|
</div>
Leerzeile
| Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. |
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
Abbildungen im Koordinatensystem
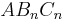 bilden eine Dreiecksschar mit dem gemeinsamen Punkt
bilden eine Dreiecksschar mit dem gemeinsamen Punkt 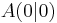 . Auf der Geraden g mit der Gleichugn
. Auf der Geraden g mit der Gleichugn 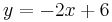 liegen die Mittelpunkte
liegen die Mittelpunkte 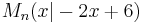 der Hyptenusen
der Hyptenusen ![\quad[AB_n]](/images/math/7/8/9/7897709debcde617572554254fb5973c.png) .
.
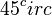 und dann eine zentrische Streckung um
und dann eine zentrische Streckung um 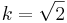 .
.
