Abschlussprüfung 2009A: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 101: | Zeile 101: | ||
|style="text-align:left" style="background-color:#EE5C42 ;"| <poem> | |style="text-align:left" style="background-color:#EE5C42 ;"| <poem> | ||
A 2.0 | A 2.0 | ||
| − | Die Pfeile <math>\vec{OP_n}={{2 \ | + | Die Pfeile <math>\vec{OP_n}(\varphi)={{2 \cos \varphi -2} \choose {0,5 \cdot \sin \varphi}}</math> und <math>\vec{OR_n}(\varphi)={{3 \cos \varphi} \choose {-3 \cdot \sin \varphi}}</math> mit <math>\quad O(0|0) </math> spannen für <math>\quad \varphi \in ]37^\circ;180^\circ[</math> Parallelogramme <math>\quad OP_nQ_nR_n</math> auf. |
| + | </poem> | ||
|} | |} | ||
{| border="1" | {| border="1" | ||
| − | |A | + | |A 2.1 Berechnen Sie die Koordinaten der Pfeile <math>\quad \vec{OP_1}</math> und <math>\quad \vec{OR_1}</math> für <math>\quad \varphi=65^\circ</math>, sowie <math>\quad \vec{OP_2}</math> und <math>\quad \vec{OR_2}</math> für <math>\quad \varphi=150^\circ</math>. Runden Sie auf zwei Stellen nach dem Komma. |
| + | Zeichnen Sie sodann die Parallelogramme <math>\quad OP_1Q_1R_1</math> und <math>\quad OP_2Q_2R_2</math> in ein Koordinatensystem ein. | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | Lösung: <math>\quad P_1</math>({ -1,15 _5}|{ 0,45 _5}; <math>\quad R_1</math>({ 1,27 _5}|{ -2,75 _5}; | ||
| + | <math>\quad P_2</math>({ -3,73 _5}|{ 0,25 _5}; <math>\quad R_2</math>({ -2,60 _5}|{ -1,50 _5}; | ||
| + | (Punktkoordinaten entsprechen Vektorkoordinaten, da <math>\quad O(0|0) </math>) | ||
| + | </quiz> | ||
| + | |||
| + | |||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Lösung"> | ||
| + | [[Bild:Peter_Fischer_09_A2.1.png]] | ||
| + | </popup> | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] | ||
| + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="600" width="850" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_09_A2.1.ggb"/> | ||
| + | </popup> | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
| + | {| border="1" | ||
| + | |A 2.2 Zeigen Sie rechnerisch, dass für die Länge der Strecken <math>\quad [OP_n</math> in Abhängigkeit von <math>\quad \varphi</math> gilt: | ||
| + | <math>\overline{OP_n}=\sqrt{3,75 \cdot \cos² \varphi-8\cdot \cos \varphi +4,25} LE</math> | ||
{| | {| | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| Zeile 129: | Zeile 161: | ||
|} | |} | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Version vom 11. Juni 2010, 12:18 Uhr
Lernpfad-Navigator
Abschlussprüfung 2009 - Aufgabe A
Leerzeile
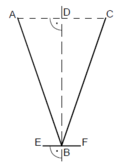
| A 1.1 Berechnen Sie das Maß des Winkels CBA. Runden Sie auf Ganze.
[Teilergebnis:
|
Leerzeile
| A 1.2 Berechnen Sie auf Millimeter gerundet, bis zu welcher Höhe der Messbecher gefüllt ist, wenn er einen halben Liter Flüssigkeit enthält.
|
Leerzeile
| Aufgabe B | |
| A 2.0 |
Leerzeile
A 2.2 Zeigen Sie rechnerisch, dass für die Länge der Strecken 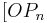 in Abhängigkeit von in Abhängigkeit von 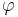 gilt: gilt:
Fehler beim Parsen(Lexikalischer Fehler): \overline{OP_n}=\sqrt{3,75 \cdot \cos² \varphi-8\cdot \cos \varphi +4,25} LE
|
Leerzeile
Weiter gehts zu Abschlussprüfung 2009 - Aufgabe B
Leerzeile
Abbildungen im Koordinatensystem
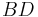 ist die Symmetrieachse.
ist die Symmetrieachse.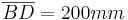 .
.
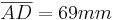 ]
]
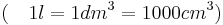

![\quad r=[AD]](/images/math/9/b/3/9b390cbd39ab6fa16a8b76d657a5d735.png) und
und 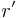 , neuer Radius.
, neuer Radius.

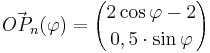 und
und 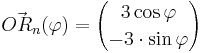 mit
mit 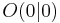 spannen für
spannen für ![\quad \varphi \in ]37^\circ;180^\circ[](/images/math/5/4/d/54d0df6d5a6a766caacaeadfb04fc212.png) Parallelogramme
Parallelogramme 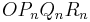 auf.
auf.
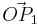 und
und 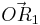 für
für 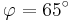 , sowie
, sowie 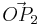 und
und 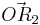 für
für 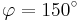 . Runden Sie auf zwei Stellen nach dem Komma.
. Runden Sie auf zwei Stellen nach dem Komma.
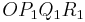 und
und 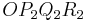 in ein Koordinatensystem ein.
in ein Koordinatensystem ein.


