Prüfungsaufgaben: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
|||
| Zeile 27: | Zeile 27: | ||
Die Bearbeitung erfoglt hauptsächlich mit Stift und Papier, allerdings möchte dir der Lernpfad GeoGebra-Applets zur Verfügung stellen und dir regelmäßig Denkanstöße in Form von Tipps geben. | Die Bearbeitung erfoglt hauptsächlich mit Stift und Papier, allerdings möchte dir der Lernpfad GeoGebra-Applets zur Verfügung stellen und dir regelmäßig Denkanstöße in Form von Tipps geben. | ||
Ob die Zeichnungen anfertigst oder nur die Applets verwendest bleibt dir überlassen, du solltest entscheiden, ob du generell Schwierigkeiten bein erstellen von Zeichnungen hast. | Ob die Zeichnungen anfertigst oder nur die Applets verwendest bleibt dir überlassen, du solltest entscheiden, ob du generell Schwierigkeiten bein erstellen von Zeichnungen hast. | ||
| + | Falls du gar nicht weißt wie du die Aufgabe lösen sollst, schau dir die Lösung an und versuche sie nachzuvollziehen. | ||
So jetzt gehts los. | So jetzt gehts los. | ||
</poem> | </poem> | ||
Version vom 11. Juni 2010, 12:50 Uhr
Prüfungsaufgaben
In der Präsentation erhälst du noch ein paar allgemeine Prüfungstipps für eine erfolgereiche Prüfung.
{{#slideshare:parallelverschiebung-100609155245-phpapp01}}
Das folgende GeoGebra-Applet zeigt dir zur Wiederholung eine Parallelverschiebung, deren Verschiebungsvektor du verändern kannst.
Leerzeile
Aufgaben
Bei der Parallelverschiebung, ebenso wie bei der orthogonalen Affinität spielt die Abbildungsmatrix eine geringere Rolle, stattdessen werden ganze Funktionen abgebildet, wie bereits in Potenzfunktionsabbildungen beschrieben. Im folgenden wartet eine ehemalige Prüfungsaufgabe auf dich.
| Aufgabe 1 Abbilden einer Exponentialfunktion. (Abschlussprüfung 2006; Wahlteil ; A1 (verändert)). Gegeben ist die Funktion f mit der Gleichung |
Der Graph der Funktion f wird durch orthogonale Affinität mit der x-Achse als Affinitätsachse und dem Affinitätsmaßstab 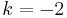 und anschließender Parallelverschiebung mit und anschließender Parallelverschiebung mit 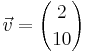 auf den Graphen zu f' abgebildet. auf den Graphen zu f' abgebildet.
Leerzeile
Leerzeile
Abbildungen im Koordinatensystem
|

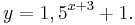
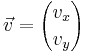 , so gilt:
, so gilt: 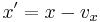 und
und 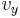 wird zu dem Funktionsterm addiert. (siehe auch Potenzfunktionsabbildungen)
wird zu dem Funktionsterm addiert. (siehe auch Potenzfunktionsabbildungen)

