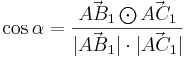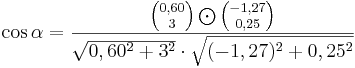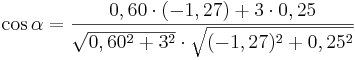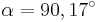Skalarprodukt: Unterschied zwischen den Versionen
| Zeile 77: | Zeile 77: | ||
{| border="1" | {| border="1" | ||
| − | |Berechnen Sie den Wert von <math>\quad \varphi</math>, sodass der Punkt C<sub>4</sub> auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C<sub>4</sub>. (<math>C_n(2\cos \varphi-1| | + | |Berechnen Sie den Wert von <math>\quad \varphi</math>, sodass der Punkt C<sub>4</sub> auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C<sub>4</sub>. (<math>C_n(2\cos \varphi-1|\sin^2 \varphi+1)</math>) |
{| | {| | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
Version vom 30. August 2010, 10:06 Uhr
Trigonometrie
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! |
{{#slideshare:skalarprodukt-100817025857-phpapp02}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Skalarprodukt
Skalarprodukt
Aufgaben
Hier hast du es ebenfalls mit alten Abschlussprüfungen zu tun. Hier sind allerdings Vektoren in Abhängigkeit eines Winkels gegeben. Um Koordinaten oder Winkel zu berechenn solltest du das Skalarprodukt verwenden!
| Aufgabe 1 Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; B2). Die Pfeile |
Für 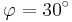 ergeben sich die Vektoren ergeben sich die Vektoren 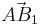 und und 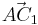 , die einen Winkel mit dem Maß , die einen Winkel mit dem Maß 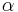 einschließen. Berechnen sie das Maß einschließen. Berechnen sie das Maß 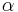 auf 2 Stellen gerundet. auf 2 Stellen gerundet.
|
Leerzeile
Berechnen Sie den Wert von 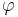 , sodass der Punkt C4 auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C4. ( , sodass der Punkt C4 auf der y-Achse liegt, und berechnen Sie die Koordinaten des Punktes C4. (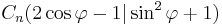 ) )
|
Leerzeile
Im rechtwinkligen Dreieck A5C5 ist die Strecke [B5C5] die Hypothenuse. Berechnen Sie den zugehörigen Wert von 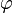 . .
|
Leerzeile
Weiter gehts zu Exkurs: Wichtiges zur Geometrie
Leerzeile
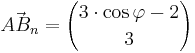 und
und 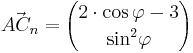 mit
mit  spannen für
spannen für ![\varphi \in [0^\circ; 180^\circ]](/images/math/3/f/f/3ffe9fc716cf41576effb3bafe19b7cc.png) Dreiecke
Dreiecke 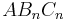 auf.
auf.