7.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
|||
| Zeile 9: | Zeile 9: | ||
{| | {| | ||
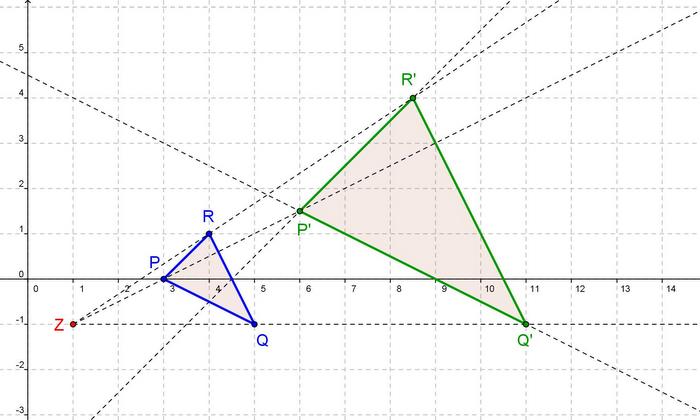
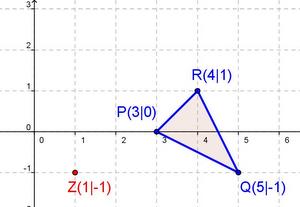
|[[Bild:Porzelt_Konstruktion_Dreieck.jpg]]||Mit Hilfe der Eigenschaften Geradentreue und Parallelentreue kann man zentrisch gestreckte Figuren wie folgt konstruieren:<br> | |[[Bild:Porzelt_Konstruktion_Dreieck.jpg]]||Mit Hilfe der Eigenschaften Geradentreue und Parallelentreue kann man zentrisch gestreckte Figuren wie folgt konstruieren:<br> | ||
| − | Zeichne ein Koordinatensystem <math>(0 \le x \le 14 ; -3 \le y \le 6)</math> mit dem Dreieck PQR und dem Zentrum Z in dein Heft. Der Streckungsfaktor beträgt k = 2,5.<br> | + | Zeichne ein Koordinatensystem <math>(0 \le x \le 14 ; -3 \le y \le 6)</math> mit dem Dreieck PQR und dem Zentrum Z in dein Heft. Der Streckungsfaktor beträgt '''k = 2,5'''.<br> |
(Die Koordinaten für die Punkte kannst du im Bild ablesen.)<br> | (Die Koordinaten für die Punkte kannst du im Bild ablesen.)<br> | ||
#Bilde den Punkt R wie gewohnt auf R' ab.<br> | #Bilde den Punkt R wie gewohnt auf R' ab.<br> | ||
Version vom 8. Juli 2009, 19:58 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
7. Station: Übung
1. Aufgabe
- Hier kannst du deine Lösung mit der von Dia vergleichen:
2. Aufgabe
- Gegeben ist eine Gerade g, die durch den Punkt A(1|2) geht und die Steigung m= 0.5 besitzt.
- a)Bestimme die Geradengleichung und zeichne die Gerade in ein Koordinatensystem ein.
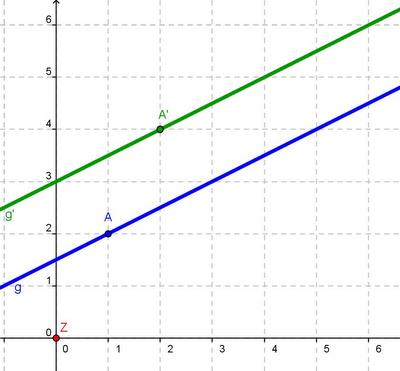
- b)Die Gerade g wird zentrisch mit Z(0|0) und k = 2 gestreckt. Konstruiere die Bildgerade g'.
- c)Berechne die Gleichung von g' mit Hilfe der zentrischen Streckung!
- Hake die richtige Lösung ab:
- Hier kannst du deine zeichnerische Lösung mit der von Dia vergleichen:
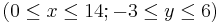 mit dem Dreieck PQR und dem Zentrum Z in dein Heft. Der Streckungsfaktor beträgt k = 2,5.
mit dem Dreieck PQR und dem Zentrum Z in dein Heft. Der Streckungsfaktor beträgt k = 2,5.