Wiederholung-1: Unterschied zwischen den Versionen
K (Höhe des GeoGebra-Applets) |
K |
||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation Wiederholungen zum Dreieck}} | ||
| + | |||
| + | |||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | {[[Bild:Dreieck.png]]"Hallo! Du kennst mich sicher noch; ich bin ein __________. } | + | {[[Bild:Dreieck.png]]"Hallo! Du kennst mich sicher noch; ich bin ein __________."} |
- Viereck | - Viereck | ||
+ Dreieck | + Dreieck | ||
| Zeile 6: | Zeile 9: | ||
</quiz> | </quiz> | ||
| − | Du hast bereits gelernt, dass ich -wie mein Name ja auch sagt- drei Eckpunkte und drei Seiten habe. Leider ist hier die Beschriftung etwas durcheinander geraten. | + | Du hast bereits gelernt, dass ich - wie mein Name ja auch sagt - drei Eckpunkte und drei Seiten habe. Leider ist hier die Beschriftung etwas durcheinander geraten. Kannst du meine Seiten bitte so beschriften, wie du es gelernt hast? |
| − | + | ||
| − | <ggb_applet height=" | + | Klicke dazu die Punkte an und ziehe sie an die richtigen Ecken im Dreieck. Prüfe anschließend dein Ergebnis. Wenn du die Punkte in die richtigen Ecken gebracht hast und prüfst, dann erscheint in der Mitte des Dreiecks ein Bild. Notiere es dir auf deinem Laufzettel! |
| + | |||
| + | <ggb_applet height="550" width="600" showResetIcon="true" filename="KS_1.Lernpfad_ggb1.ggb" /> | ||
<br /><br /> | <br /><br /> | ||
| Zeile 19: | Zeile 23: | ||
Danke, so schaut das Ganze doch schon viel ordentlicher aus. | Danke, so schaut das Ganze doch schon viel ordentlicher aus. | ||
<br /> | <br /> | ||
| + | |||
| + | |||
| + | |||
<div class="schuettel-quiz"> Jetzt fehlt aber noch eine Art der Bestimmungsstücke, nämlich die '''winkel''' </div> | <div class="schuettel-quiz"> Jetzt fehlt aber noch eine Art der Bestimmungsstücke, nämlich die '''winkel''' </div> | ||
<br /> | <br /> | ||
| Zeile 29: | Zeile 36: | ||
</div> | </div> | ||
| − | Kannst du diese Buchstaben auch noch den richtigen Winkeln zuordnen? | + | Kannst du diese Buchstaben auch noch den richtigen Winkeln zuordnen?<br />''Ziehe dazu die passenden Felder in die grünen Lücken hinter den Buchstaben A, B und C.'' |
| − | ''Ziehe dazu die passenden Felder in die grünen Lücken hinter den Buchstaben A, B und C.'' | + | |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
{| | {| | ||
| Zeile 44: | Zeile 50: | ||
</div> | </div> | ||
| − | Das war ja bisher noch nicht so schwer. | + | Das war ja bisher noch nicht so schwer. Hier findest du die drei Sätze etwas übersichtlicher: {{versteckt|<br /> |
| − | <br /><br /> | + | Der Winkel an der Ecke A heißt α und wird gebildet von den Seiten b und c. [[Bild:KS_1.Lernpfad_Winkel1.png]]<br /><br /><br /> |
| − | + | Der Winkel an der Ecke B heißt β und wird gebildet von den Seiten a und c. [[Bild:KS_1.Lernpfad_Winkel2.png]]<br /><br /><br /> | |
| + | Der Winkel an der Ecke C heißt γ und wird gebildet von den Seiten a und b. [[Bild:KS_1.Lernpfad_Winkel3.png]] | ||
| + | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | + | Zur Erinnerung findest du hier nochmal ein Bild von einem Dreieck mit den üblichen Bezeichnungen der Ecken, Seiten und Winkel. {{versteckt|[[Bild:Merke1.png]]}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | }} | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Aufgabe-Mathe|Übertrage die Bezeichnungen in das Dreieck auf deinem <u>Laufzettel</u>! | |
| − | { | + | '''}} |
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | }} | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | [[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck/Wiederholung-2|<math>\Rightarrow</math> Wenn du damit fertig bist, geht es hier weiter.]] |
Aktuelle Version vom 26. Februar 2010, 18:35 Uhr
Du hast bereits gelernt, dass ich - wie mein Name ja auch sagt - drei Eckpunkte und drei Seiten habe. Leider ist hier die Beschriftung etwas durcheinander geraten. Kannst du meine Seiten bitte so beschriften, wie du es gelernt hast?
Klicke dazu die Punkte an und ziehe sie an die richtigen Ecken im Dreieck. Prüfe anschließend dein Ergebnis. Wenn du die Punkte in die richtigen Ecken gebracht hast und prüfst, dann erscheint in der Mitte des Dreiecks ein Bild. Notiere es dir auf deinem Laufzettel!
ACHTUNG:
Die Ecke, die der Seite a gegenüberliegt heißt A,
die Ecke, die der Seite b gegenüberliegt heißt B,
die Ecke, die der Seite c gegenüberliegt heißt C.
Danke, so schaut das Ganze doch schon viel ordentlicher aus.
Die Winkel werden normalerweise mit den Buchstaben α, β und γ bezeichnet.
Aus welcher Sprache stammen sie?
(!Chinesisch) (Griechisch) (!Afrikanisch) (!Deutsch)
Kannst du diese Buchstaben auch noch den richtigen Winkeln zuordnen?
Ziehe dazu die passenden Felder in die grünen Lücken hinter den Buchstaben A, B und C.
| Der Winkel an der Ecke ___ | heißt ___ | und wird gebildet von den Seiten ___ |
| A | α | b und c |
| B | β | a und c |
| C | γ | a und b |
Das war ja bisher noch nicht so schwer. Hier findest du die drei Sätze etwas übersichtlicher:
Der Winkel an der Ecke A heißt α und wird gebildet von den Seiten b und c. 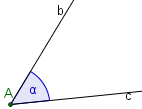
Der Winkel an der Ecke B heißt β und wird gebildet von den Seiten a und c. 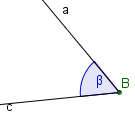
Der Winkel an der Ecke C heißt γ und wird gebildet von den Seiten a und b. 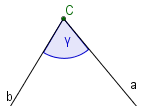
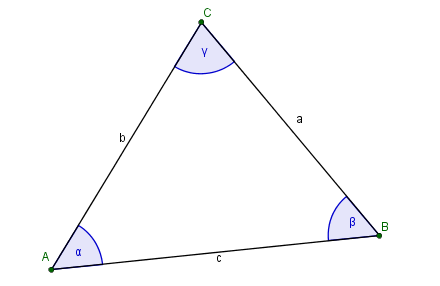
Zur Erinnerung findest du hier nochmal ein Bild von einem Dreieck mit den üblichen Bezeichnungen der Ecken, Seiten und Winkel.
|
Übertrage die Bezeichnungen in das Dreieck auf deinem Laufzettel! |
 Wenn du damit fertig bist, geht es hier weiter.
Wenn du damit fertig bist, geht es hier weiter.
