Logarithmus: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(- Doppelung) |
(Vorlage verwendet) |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Exponential- und Logarithmusfunktion}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<!-- | <!-- | ||
==Logarithmus==--> | ==Logarithmus==--> | ||
| Zeile 35: | Zeile 16: | ||
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| − | {{pdf|Peter Fischer_Logarithmusfunktion | + | {{pdf|Peter Fischer_Logarithmusfunktion.pdf|Logarithmus}} |
| Zeile 130: | Zeile 111: | ||
<poem> | <poem> | ||
| − | '''Weiter gehts zu Abschnitt III [[Trigonometrie]]''' | + | '''Weiter gehts zu Abschnitt III [[../../Trigonometrie|Trigonometrie]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 136: | Zeile 117: | ||
<div style="background:#66CD00;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Exponential- & Logarithmusfunktion</div> | <div style="background:#66CD00;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Exponential- & Logarithmusfunktion</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#66CD00; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#66CD00; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Exponential- | + | [[../../|LERNPFAD]] | [[../|Exponential- und Logarithmusfunktion]] | [[../Logarithmus|Logarithmus]] </div> |
Aktuelle Version vom 15. Oktober 2011, 12:25 Uhr
Lernpfad-Navigator
| Arbeitsauftrag
Der Logarithmus hat für uns zwei Bedeutungen:
Auf den folgenden Folien wirst du an beide Aspekte erinnert. |
{{#slideshare:logarithmusfunktion-100817023437-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Logarithmus
Logarithmus
Leerzeile
Aufgaben
Die folgenden Aufgaben beziehen sich auf Exponentialgleichungen, x-Wertberechnungen von Exponentialfunktionen, da dies für deine Prüfung sehr relevant ist.
| Aufgabe 1
Berechne Parameter und x-Werte zu Exponentialfunktionen. (Abschlussprüfung 2007; Aufgabengruppe B; 1.1) |
Leerzeile
Die Rakete mit 22,0 t Startmasse hat seit dem Start 10,0 t Treibstoff verbrannt. Berechnen sie die dabei erreichte Geschwindigkeit x 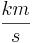 . .
|
Leerzeile
| Aufgabe 2 Löse folgende Exponentialgleichungen (Abschlussprüfung 2004; Aufgabengruppe A; 1.6) |
Eine Sekunde nach dem Beginn der Aufladung des Kondensators, wird ein zweiter Kondensator entladen. Dieser Vorgang wird mit der Gleichung 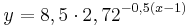 beschrieben. Dabei steht x s für die Zeit ab dem Beginn der Aufladung des ersten Kondensators. Berechnen Sie auf Hundertstel Sekunden gerundet die Zeit x s, nach der an beiden Kondensatoren die gleiche Spannung anliegt. beschrieben. Dabei steht x s für die Zeit ab dem Beginn der Aufladung des ersten Kondensators. Berechnen Sie auf Hundertstel Sekunden gerundet die Zeit x s, nach der an beiden Kondensatoren die gleiche Spannung anliegt.
|
Leerzeile
Löse die Exponentialgleichung 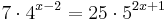 . .
|
Weiter gehts zu Abschnitt III Trigonometrie
Leerzeile
Exponential- & Logarithmusfunktion
LERNPFAD | Exponential- und Logarithmusfunktion | Logarithmus
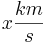 . Dabei verringert sich die Masse
. Dabei verringert sich die Masse  (Tonne) der Rakete durch den Ausstoß von verbranntem Treibstoff. Die Veränderung der Raketenmasse in Abhängigkeit von ihrer Geschwindigkeit kann durch eine Gleichung der Form
(Tonne) der Rakete durch den Ausstoß von verbranntem Treibstoff. Die Veränderung der Raketenmasse in Abhängigkeit von ihrer Geschwindigkeit kann durch eine Gleichung der Form 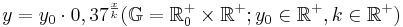 dargestellt werden, wobei
dargestellt werden, wobei 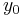 die Startmasse der Rakete ist und
die Startmasse der Rakete ist und 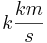
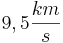 erreicht, hat sich die Masse auf 4 t verringert. Berechnen sie k.
erreicht, hat sich die Masse auf 4 t verringert. Berechnen sie k.
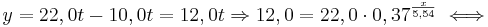
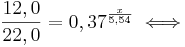
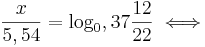
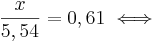
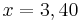
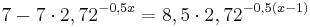 lösen zu können brauchst du die Potenzgesetze!
lösen zu können brauchst du die Potenzgesetze!