Eigenschaften der zentrischen Streckung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(1. Station) |
|||
| Zeile 3: | Zeile 3: | ||
===Eigenschaften der zentrischen Streckung=== | ===Eigenschaften der zentrischen Streckung=== | ||
}} | }} | ||
| + | <br>[[Bild:Porzelt_Eigenschaften.jpg|right]] | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | :[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/2.Station|2. Station: Geradentreue und Parallelentreue]] | ||
| + | ::[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]] | ||
| + | :::[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/4.Station|4. Station: Längenverhältnistreue]] | ||
| + | ::::[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/5.Station|5. Station: Kreistreue]] | ||
| + | :::::[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/6.Station|6. Station: Zusammenfassung]] | ||
| + | ::::::[[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/7.Station|7. Station: Übung]] | ||
| + | |||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
<br> | <br> | ||
| − | |||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
==1. Station: Fixelemente== | ==1. Station: Fixelemente== | ||
Version vom 3. Juli 2009, 16:25 Uhr
 Lernpfad
|
1. Station: Fixelemente
- Für k
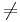1 gilt:
- Das Streckungszentrum Z ist Fixpunkt, da es immer auf sich selbst abgebildet wird.
- Betrachte das Bild und überleg dir, wie die Geraden f' und g' verlaufen, wenn man f und g an dem Zentrum Z zentrisch streckt.
- Hier kannst du deine Lösung mit der von Dia vergleichen:
- f' wird auf f und g' wird auf g abgebildet. Geometrisch bedeutet dies: f=f' und g=g'.
- Panto will auch etwas dazu sagen. Lass es dir anzeigen:
- Alle Geraden die durch den Punkt Z verlaufen sind Fixgeraden. Sie werden bei einer zentrischen
- Streckung auf sich selbst abgebildet.
