7.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| + | [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung|1. Station: Fixelemente]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/2.Station|2. Station: Geradentreue und Parallelentreue]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/4.Station|4. Station: Längenverhältnistreue]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/5.Station|5. Station: Kreistreue]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/6.Station|6. Station: Zusammenfassung]] - [[Benutzer:Leonie Porzelt/Eigenschaften der zentrischen Streckung/7.Station|7. Station: Übung]] | ||
| + | </div> | ||
| + | |||
==7. Station: Übung== | ==7. Station: Übung== | ||
{| | {| | ||
Version vom 3. Juli 2009, 16:52 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
7. Station: Übung
- Hier kannst du deine Lösung mit der von Dia vergleichen:
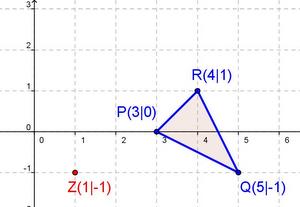
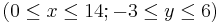 mit dem Dreieck PQR und dem Zentrum Z in dein Heft.
mit dem Dreieck PQR und dem Zentrum Z in dein Heft.